(2 семестр)
Номера даются по задачнику А.М. Зубкова,Б.А. Севастьянова и
В.П. Чистякова 1989 г. изд. (в скобках – по задачнику 1980 г. изд.)
1. Заполнить графу «Характеристическая функция» в Таблице.
2. Характеристическая функция случайной величины 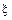 имеет вид:
имеет вид:
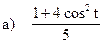 ;
;  б)
б) 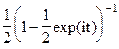 ; в)
; в) 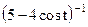 .
.
Найти распределение 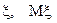 и
и 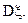
3. Характеристическая функция случайной величины 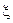 имеет вид:
имеет вид:
а) 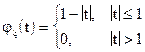 ; б)
; б) 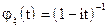 .
.
Найти распределение 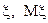 и
и 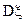 .
.
4‘. Функцией распределения случайной величины 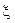 является канторова лестница. Найти характеристическую функцию
является канторова лестница. Найти характеристическую функцию 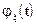 .
.
5. Являются ли характеристическими следующие функции? (Если да - то для какой случайной величины, если нет - то почему?)
а) 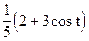 б)
б) 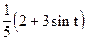 в)
в) 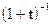 г)
г) 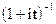
д) 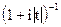 е)
е) 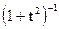 ж)
ж) 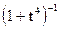 з) ‘
з) ‘ 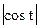
6. Величины 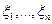
 независимы и имеют экспоненциальное распределение
независимы и имеют экспоненциальное распределение 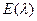 . Найти распределение и все моменты суммы
. Найти распределение и все моменты суммы 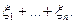
7. Найти плотность распределения 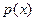 , удовлетворяющую уравнению
, удовлетворяющую уравнению 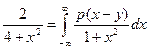 .
.
8. № 4.157 (4.139)
9. № 4.132 (4.122)
10. Пусть 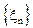 - последовательность независимых случайных величин, имеющих распределение
- последовательность независимых случайных величин, имеющих распределение
Коши 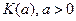 . Найти распределение величины
. Найти распределение величины 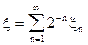 .
.
11. Крутой стрелок попадает в мишень с любой руки с вероятностью 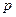 , а чтобы определить, с какой руки стрелять, он бросает симметричную монету. Найти распределение числа выстрелов с
, а чтобы определить, с какой руки стрелять, он бросает симметричную монету. Найти распределение числа выстрелов с
правой руки, если стрельба ведется до первого попадания.
12.‘ Пусть 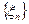 - последовательность независимых одинаково распределенных целочисленных
- последовательность независимых одинаково распределенных целочисленных
величин и пусть 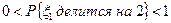 . Доказать, что
. Доказать, что 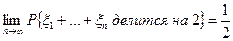 .
.
 8
8
13. № 4.4 (4.4)
14. Применим ли закон больших чисел к последовательности независимых случайных величин 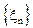 таких, что
таких, что 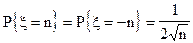 ,
, 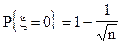 .
.
15. Пусть 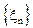 - последовательность независимых случайных величин,
- последовательность независимых случайных величин, 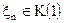 ,
, 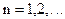 Найти предельное распределение величин
Найти предельное распределение величин 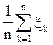 при
при 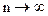 . Как это согласуется с законом больших чисел?
. Как это согласуется с законом больших чисел?
16. Пусть 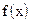 - непрерывная ограниченная функция. С помощью закона больших чисел вычислить
- непрерывная ограниченная функция. С помощью закона больших чисел вычислить
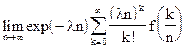 .
.
17‘. Пусть 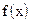 - непрерывная ограниченная функция. Вычислить
- непрерывная ограниченная функция. Вычислить
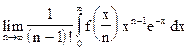 .
. 
 18. Пусть
18. Пусть 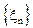 - последовательность независимых случайных величин,
- последовательность независимых случайных величин, 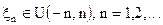 Применима ли к этой последовательности центральная предельная теорема?
Применима ли к этой последовательности центральная предельная теорема?
19. В предположении, что размер одного шага пешехода равномерно распределен в интервале от 70 до 80 см и размеры шагов независимы, найти вероятность того, что он пройдет расстояние не меньшее 7.49 км и не большее 7.51 км, сделав 10000 шагов.
20. Сколько раз нужно бросить игральную кость, чтобы с вероятностью, не меньшей 0.95, сумма выпавших очков превысила 400?
21. Пусть 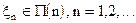 .С помощью центральной предельной теоремы доказать, что
.С помощью центральной предельной теоремы доказать, что 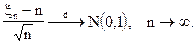
22. Вовочка пришел в тир, в котором за каждое попадание в цель выдают дополнительный патрон, а если число попаданий превысит 70, то еще и бюст любимого учителя математики. Вовочка с детства сильно мечтал о таком бюсте, поэтому он купил 100 патронов и стрелял до тех пор, пока все (и купленные и дополнительные) патроны не кончились. Найти вероятность осуществления Вовочкиной мечты, если в каждом выстреле он попадает с вероятностью 0.4.
23. С помощью центральной предельной теоремы найти 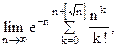 где
где 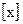 -целая часть x.
-целая часть x.
24‘. Вычислить 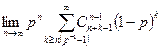 .
.
25. Вычисление интеграла 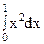 производится методом Монте-Карло. Сколько нужно произвести испытаний, чтобы с вероятностью, не меньшей 0.99, погрешность вычисления не превзошла 0.01?
производится методом Монте-Карло. Сколько нужно произвести испытаний, чтобы с вероятностью, не меньшей 0.99, погрешность вычисления не превзошла 0.01?
26. Пусть 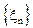 - последовательность независимых одинаково распределенных случайных величин,
- последовательность независимых одинаково распределенных случайных величин, 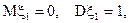 а случайная величина
а случайная величина 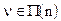 не зависит от
не зависит от 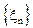 . Найти предельное распределение величин
. Найти предельное распределение величин 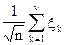 при
при 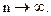
27. Пусть 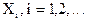 - случайные числа, наудачу и независимо друг от друга выбранные из совокупности
- случайные числа, наудачу и независимо друг от друга выбранные из совокупности 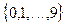 .
.
а) Пусть 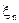 - число различных чисел среди первых n выбранных. Показать, что
- число различных чисел среди первых n выбранных. Показать, что 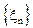 - цепь Маркова и дать классификацию состояний.
- цепь Маркова и дать классификацию состояний.
б) Пусть 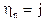 , если произведение
, если произведение 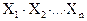 оканчивается на цифру j. Показать, что
оканчивается на цифру j. Показать, что 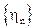 - цепь Маркова и дать классификацию состояний.
- цепь Маркова и дать классификацию состояний.
28. Матрица вероятностей перехода за 1 шаг имеет вид:
а) 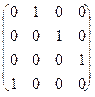 б)
б) 
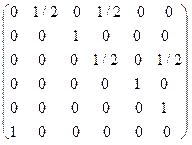 в)
в) 
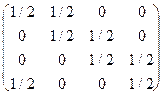
Будут ли соответствующие цепи Маркова периодическими и, если да, то с каким периодом?
29. № 5.50 (5.1) 30. № 5.56 (нет)
31. № 5.75 (5.17) 32. № 5.62 (5.11)
33. Найти 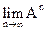 , если
, если 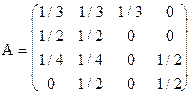 .
.
34‘. Простейшая модель естественного отбора. На изолированном острове численность некоторого вида не может превзойти N из-за ограниченности запасов пищи. Предположим, что рождается мутант с несколько лучшими данными для выживания и в каждом следующем поколении каждый мутант завоевывает себе место с вероятностью p>1/2 и теряет место с вероятностью q=1-p. Найти вероятность того, что когда-нибудь мутанты овладеют островом.
35. У однородной цепи Маркова 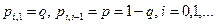 Доказать существование
Доказать существование
пределов 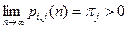 и найти их.
и найти их.
36. У однородной цепи Маркова 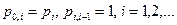 и
и 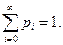 При каких условиях существуют пределы
При каких условиях существуют пределы 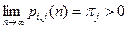 ? Найти эти пределы.
? Найти эти пределы.
37. Ливень космических частиц вызван попаданием в начальный момент времени в атмосферу одной частицы. Определить вероятность того, что в момент времени t будет n частиц, если каждая частица в промежутке времени 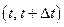 с вероятностью
с вероятностью 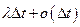 может вызвать возникновение новой частицы и с вероятностью
может вызвать возникновение новой частицы и с вероятностью 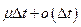 может исчезнуть.
может исчезнуть.
38. Один рабочий обслуживает m автоматических станков, которые при нормальной работе не требуют его вмешательства. Остановки каждого станка вследствие неполадок образуют простейший поток с параметром 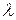 , не зависящий от потоков неполадок других станков. Для устранения неполадки рабочий тратит случайное время, распределенное по показательному закону с параметром
, не зависящий от потоков неполадок других станков. Для устранения неполадки рабочий тратит случайное время, распределенное по показательному закону с параметром 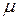 . Найти предельные (при
. Найти предельные (при 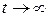 ) вероятности того, что k станков не работают (ремонтируются или ожидают ремонта) и математическое ожидание числа станков в очереди на ремонт.
) вероятности того, что k станков не работают (ремонтируются или ожидают ремонта) и математическое ожидание числа станков в очереди на ремонт.
39. Система обслуживания состоит из n аппаратов, каждый из которых обслуживает одновременно лишь одно требование. Время обслуживания является показательно распределенной случайной величиной с параметром 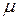 . В систему поступает простейший поток требований с параметров
. В систему поступает простейший поток требований с параметров 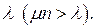 Обслуживание начинается немедленно, если есть хотя бы один свободный аппарат. Если все аппараты заняты, а число требований в очереди на обслуживание менее m, то вновь поступившее требование становится в очередь; если же в очереди m требований, то это требование получает отказ.
Обслуживание начинается немедленно, если есть хотя бы один свободный аппарат. Если все аппараты заняты, а число требований в очереди на обслуживание менее m, то вновь поступившее требование становится в очередь; если же в очереди m требований, то это требование получает отказ.
Определить предельные значения:
а) вероятности того, что в системе обслуживания ровно k требований;
б) вероятности того, что вновь поступившее требование получит отказ;
в) вероятности того, что все обслуживающие аппараты будут заняты;
г) распределения времени ожидания начала обслуживания;
д) математическое ожидание числа требований, ожидающих начала обслуживания, числа требований, находящихся в системе обслуживания и числа свободных от обслуживания аппаратов.
40. Парикмахерская имеет трех мастеров, каждый из которых в среднем на обслуживание одного клиента тратит 10 минут (время обслуживания имеет показательное распределение). Клиенты образуют простейший поток, со средним числом поступлений 12 человек в час. Клиенты становятся в очередь, если к моменту их прихода в очереди менее трех человек, в противном случае они покидают парикмахерскую.
Определить предельные значения:
а) вероятности отсутствия клиентов в парикмахерской;
б) вероятности того, что клиент покинет парикмахерскую необслуженным;
в) вероятности того, что все мастера будут заняты работой;
г) средне число клиентов в очереди и среднее число клиентов в парикмахерской.
а) 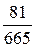 ; б)
; б) 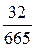 ; в)
; в) 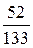 ; г)
; г) 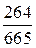 и
и 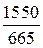 .
.
Примечание. Знаком ‘ отмечены призовые задачи.