Любое уравнение, которое требуется решить в целых числах, называется
диофантовым уравнением. Александрийский математик Диофант, живший около 2 тысяч
лет тому назад, описал общие методы решения таких уравнений в своей книге «Арифметика». Диофантовы уравнения имеют, как правило, много решений, поэтому их называют неопределенными уравнениями, а решения таких уравнений записывают в общем виде с использованием целочисленного параметра.
Можно условно выделить следующие методы решения диофантовых уравнений: метод полного перебора всех возможных значений переменных, входящих в уравнение; метод разложения на множители; метод, основанный на выражении одной переменной через другую и выделении целой части дроби; методы, основанные на выделении полного квадрата; метод решения уравнения с двумя переменными как квадратного относительно одной из переменных; метод, основанный на оценке выражений, входящих в уравнение; метод, основанный на алгоритме Евклида; метод, основанный на теории цепных дробей; метод, основанный на теории сравнений; метод бесконечного спуска и др.
При подготовке к ЕГЭ (19 задача), необходимо уметь решать линейные и квадратные Диофантовы уравнения. Рассмотрим несколько универсальных методов решения уравнений в целых числах.
В школьных учебниках можно встретить следующую теорему: Линейное диофантово уравнение ах+bу=с, где а, b, с∈Z имеет решение тогда и только тогда, когда с делится на НОД чисел а и b. Если d =НОД (а, b), a=a1d, b=b1d, c=c1d и (x0, y0) – некоторое решение уравнения ах+bу=с, то все решения задаются формулами х=x0+b1t, y=y0–a1t, где t ─ произвольное целое число.
Пример 1. Существует ли целое число, которое при делении на 12 даёт в остатке 5, а при делении на 8 даёт в остатке 3?
Решение: Если число 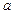 при делении на 12 дает остаток 5, то
при делении на 12 дает остаток 5, то  , где
, где 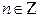 . Аналогично
. Аналогично 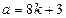 , где
, где 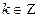 . Приравняем значения для
. Приравняем значения для 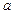 и решим уравнение в целых числах.
и решим уравнение в целых числах.
12n + 5 = 8k + 3 Û 12n – 8k = –2 – решений нет, так как левая часть кратна 4, а правая – нет.
Ответ: Не существует.
Пример 2. (Олимпиада МГУ, 1969) Остаток от деления некоторого натурального числа n на 6 равен 4, остаток от деления n на 15 равен 7. Чему равен остаток от деления числа n на 30?
Решение: Из условия примера получим систему уравнений 
Отсюда 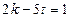 .
.
Так как НОД(2,5)=1, то решение имеется. Найдем какое-нибудь частное решение (k,t), например, пара (3,1) - решение, тогда все остальные решения задаются в виде 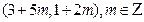
Осталось подставить найденные (k,t) в систему 
Следовательно, остаток от деления n на 30 равен 22.
Ответ: 22
Для тех, кто не уверен, что сможет на ЕГЭ вспомнить формулы, по которым задаются общие решения диофантовых уравнений через частное решение, предлагаю освоить метод решения линейных уравнений, основанный на алгоритме Евклида, который еще называют метод спуска. Метод спуска предполагает сначала последовательное выражение одной переменой через другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств, для получения общего решения уравнения.
Пример 3: (ЕГЭ, 2010) Найти все целые решения уравнения 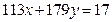 , удовлетворяющие неравенствам
, удовлетворяющие неравенствам  .
.
Решение:
Выберем неизвестное, имеющее наименьший по модулю коэффициент (в нашем случае это x), и выразим его через другое неизвестное: 
Выделим целую часть: 
Очевидно, что x будет целым, если выражение  окажется целым,
окажется целым,
что, в свою очередь, будет иметь место тогда, когда число 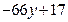 без
без
остатка делится на 113. Введем дополнительную целочисленную переменную  следующим образом:
следующим образом:  . В результате получили уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.
. В результате получили уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.
Далее предлагается повторить все те же действия, только уже с новым уравнением до тех пор, пока представлении переменной не останется дробей.
Вновь выразим переменную с меньшим по модулю коэффициентом и выделим ее целую часть, в данном случае это переменная  :
:  .
.
Чтобы  было целым, надо потребовать, чтобы «хвостик»
было целым, надо потребовать, чтобы «хвостик» 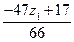 был целым числом, для этого
был целым числом, для этого 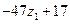 должно быть кратно
должно быть кратно  , тогда введем новую переменную
, тогда введем новую переменную  такую что
такую что  . И рассмотрим теперь уже это уравнение по предложенному алгоритму. Выразим переменную с наименьшим по модулю коэффициентом:
. И рассмотрим теперь уже это уравнение по предложенному алгоритму. Выразим переменную с наименьшим по модулю коэффициентом:  . Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную
. Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную 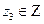 такую что
такую что  . Выразим переменную с меньшим по модулю коэффициентом:
. Выразим переменную с меньшим по модулю коэффициентом:  . Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную
. Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную 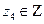 такую что
такую что  . Выразим переменную с меньшим по модулю коэффициентом:
. Выразим переменную с меньшим по модулю коэффициентом:  . Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную
. Потребуем, чтобы «хвостик» был целым, введем новую целочисленную переменную  такую что
такую что  . Выразим переменную с меньшим по модулю коэффициентом:
. Выразим переменную с меньшим по модулю коэффициентом:  . Видим, что в представлении переменной нет больше дробей, «спуск» закончен. Тогда обозначим последнюю введенную переменную
. Видим, что в представлении переменной нет больше дробей, «спуск» закончен. Тогда обозначим последнюю введенную переменную  , и начнем «подъем». В обратном порядке возвращаемся к исходным переменным и выражаем их через
, и начнем «подъем». В обратном порядке возвращаемся к исходным переменным и выражаем их через 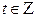 .
.
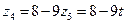

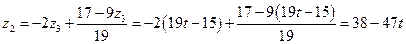


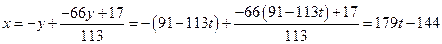
Решением уравнения в целых числах будут все пары чисел  записанные в общем виде
записанные в общем виде  , где
, где 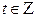 .
.
Приняв во внимание условия  находим
находим  т.е.
т.е.  , тогда
, тогда  .
.
Ответ: 
Здесь сделаем два замечания. Во-первых, решения уравнения может выглядеть по-разному, так как 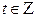 .Например, запись
.Например, запись  и
и  задают одно и то же множество решений. При первой записи пару решений
задают одно и то же множество решений. При первой записи пару решений  мы получаем при
мы получаем при  , а при второй записи эту же пару решений получим при
, а при второй записи эту же пару решений получим при 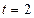 .
.
Во-вторых, такие «глубокие спуски», как представлено в третьем примере, встречаются крайне редко. Давайте решим методом «спуска» уравнение из второго примера: 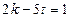 . Выбираем меньший по модулю коэффициент,
. Выбираем меньший по модулю коэффициент,  , выражаем переменную и выделяем целую часть
, выражаем переменную и выделяем целую часть 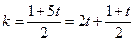 , «хвостик» должен быть целым, вводим новую переменную
, «хвостик» должен быть целым, вводим новую переменную  , где
, где  , тогда
, тогда  и
и  . Спуск закончен, так как в выражении для
. Спуск закончен, так как в выражении для  нет дробей. Начинаем подъем. Подставим выражение
нет дробей. Начинаем подъем. Подставим выражение  . Тогда решением уравнения
. Тогда решением уравнения 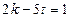 в целых числах будут пары
в целых числах будут пары 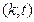 заданные в виде
заданные в виде  . Понятно, что
. Понятно, что  задает такое же множество решений уравнений, что и
задает такое же множество решений уравнений, что и  .
.
Пример 4. Решить в натуральных числах уравнение  .
.
Решение: При решении нелинейных уравнений, необходимо ограничить перебор различных вариантов. Для этого используют различные методы, например, разложение на множители. 

Понимаем, что в скобках стоят целые числа и перебираем все возможные целые множители, произведение которых равно 18. Причем, во второй скобке стоит натуральное число, а множители должны быть одного знака, тогда и первая скобка должна быть положительна, поэтому все варианты с отрицательными множителями нам не подходят.





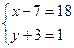 .
.
Выбирая подходящие решения в виде натуральных чисел, получаем следующий ответ: 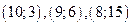 .
.
Ответ: 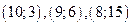 .
.