Вероятность и графы
Теория вероятностей.
Теория вероятностей – это математическая наука, изучающая закономерности в массовых случайных явлениях.
До появления теории вероятностей как общепризнанной теории в науке господствовал детерминизм, согласно которому осуществление определенного комплекса условий однозначно определяет результат. Классическим примером является механика. Например, на основании законов небесной механики по известному в некоторый момент положению планет Солнечной системы могут быть очень точно предсказаны солнечные и лунные затмения. Подобные законы называются детерминированными законами.
Однако практика показала, что этот подход далеко не всегда применим. Не все явления макромира поддаются точному предсказанию, несмотря на то, что наши знания о нем непрерывно уточняются и углубляются. Еще менее детерминированы законы и закономерности микромира.
Математические законы теории вероятностей отражают реальные статистические законы, объективно существующие в массовых случайных явлениях.
Современное развитие теории вероятностей характеризуется всеобщим подъемом интереса к ней и расширением круга ее приложений. Одной из важнейших сфер приложения теории вероятностей является экономика. В настоящее время сложно представить себе исследование и прогнозирование экономических явлений без привлечения опирающихся на теорию вероятности методов эконометрического моделирования, регрессионного анализа, трендовых и других моделей.
Вероятность события вычисляется путем сложения вероятностей благоприятного исхода, которую в свою очередь определяем произведением вероятностей каждого ребра, соответствующего этому благоприятному событию.
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий и они формулировались в наглядных представлениях. Важный вклад в теорию вероятностей внёс Яков Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Например: определить однозначно результат выпадения орла или решки в результате подбрасывания монеты нельзя, но при многократном подбрасывании выпадает примерно одинаковое число орлов и решек.
Испытанием называется реализация определенного комплекса условий, который может воспроизводиться неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которого в каждом испытании приводит к неоднозначности исхода испытания.
Например: испытание - подбрасывание монеты.
Результатом испытания является событие. События бывают:
- Достоверные (всегда происходят в результате испытания);
- Невозможные (никогда не происходят);
- Равновероятные (имеют равные возможности произойти), менее вероятные и более вероятные;
- Случайные (могут произойти или не произойти в результате испытания).
Например: При подбрасывании кубика невозможное событие - кубик станет на ребро, случайное событие - выпадение какой либо грани, равновероятное событие - кубик станет на четную грань.
Конкретный результат испытания называется элементарным событием.
В результате испытания происходят только элементарные события.
Совокупность всех возможных, различных, конкретных исходов испытаний называется пространством элементарных событий.
Например: Испытание - подбрасывание шестигранного кубика. Элементарное событие - выпадение грани с 1 или 2.
Совокупность элементарных событий это пространство элементарных событий.
Сложным событием называется произвольное подмножество пространства элементарных событий.
Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному.
Таким образом, если в результате испытания может произойти только одно элементарное событие, то в результате испытания происходят все сложные события, в состав которых входят эти элементарные.
Например: испытание - подбрасывание кубика.
Элементарное событие - выпадение грани с номером 1. Сложное событие - выпадение нечетной грани.
Классическое определение вероятности.
ТЕОРЕМА
Пусть пространство элементарных событий состоит из их конечного числа и все элементарные события равновероятны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания, следовательно, их можно считать равновероятными.
Пусть х - произвольное событие.
А1, А2, …, Аn - группа событий, где n - количество событий.
Аi - любое из событий группы, которое приводит к наступлению события х.
Тогда Аi, называется благоприятствующим и вероятное событие определяется
где m - число элементарных событий, n - общее число элементарных событий, то есть:
Если элементарные события являются равноправными, а, следовательно, и равновероятными, то вероятность наступления произвольного события равна дроби, числитель которой равен числу элементарных событий, входящих в данное, а знаменатель - общее число элементарных событий. Такое определение вероятности было дано впервые в работах французского математика Лапласа, и называется классическим.
Для того чтобы закрепить вышеизложенную информацию, мы подробно решим одну простую задачу, а именно рассмотрим случайный эксперимент, который может завершиться одним из возможных исходов, причем пары этих исходов равновероятные. Данный эксперимент можно легко провести дома и подтвердить полученные результаты.
Одновременно бросаются 3 монеты. Определить вероятность того, что:
1) Выпадут 3 орла;
2) Выпадут 2 орла и 1 решка;
3) Выпадут 2 решки и 1 орёл;
4) Выпадут 3 решки.
Решение
1) 0,5*0,5*0,5=0,125
2) (0,5*0,5*0,5)*3=0,375
3) (0,5*0,5*0,5)*3=0,375
4) 0,5*0,5*0,5=0,125
Пояснение
Приведем всевозможные исходы всех бросков монет в таблице:
| Первая монета | Вторая монета | Третья монета |
| Орёл | Орёл | Орёл |
| Орёл | Орёл | Решка |
| Орёл | Решка | Орёл |
| Орёл | Решка | Решка |
| Решка | Орёл | Орёл |
| Решка | Орёл | Решка |
| Решка | Решка | Орёл |
| Решка | Решка | Решка |
Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них красные, 3-синие и 1-белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появление цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Определение (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
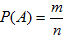 (1)
(1)
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Пример 1. Найти вероятность события А={появление не менее пяти очков при одном бросании игральной кости}.
Используем формулу (1). В нашем случае число возможных исходов n=6, а число, благоприятствующих этому событию исходов, m=2. То есть P(A)=2/6=1/3. Итак, вероятность появления не менее пяти очков при одном бросании игральной кости равна 0.33 или 1/3
Из определения вероятности вытекают следующие ее свойства:
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1
Свойство 2. Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно:
0<P(A)<1
Итак, вероятность любого события удовлетворяет двойному неравенству:
0  P(A)
P(A)  1
1
Теория графов.
Графы оказались хорошей математической моделью широкого класса объектов и процессов. Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электроника, машиностроение, архитектура, исследование операций, генетика, психология, социология, экономика, антропология и лингвистика. При этом обычно на графе решаются задачи о достижимости, задачи сетевого планирования, потоковая задача.
Цель исследования, осуществляемого в данной работе, - совершенствование процесса оптимизации сложных задач экономического и сетевого планирования путем разработки технологий и программных средств, использующих графовое моделирование.
Сформулированная цель предопределила следующую совокупность решаемых задач:
1.Исследовать эффективность стандартных алгоритмов решения задач оптимизации;
2.Разработать и реализовать алгоритмы, позволяющие автоматизировать решение задач оптимизации;
3.Реализовать разработанную процедуру в виде программного продукта, соответствующего современным требованиям;
4.Провести исследование эффективности разработанной процедуры на представительном множестве тестовых задач;
5.Установить параметры, существенно влияющие на эффективность разработанной процедуры, и выработать рекомендации по их настройке;
6.Провести апробацию разработанного подхода на реальных практических задачах.
Объект исследования - графовые методы в теории информации.
Предмет исследования - модели структур и сложность решения задач оптимизации.
Использованные методы исследования: теоретический анализ математической литературы, учебников и учебных пособий; изучение и анализ состояния исследуемой проблемы в теоретических основах информатики и дискретной математике; при выполнении работы использовался аппарат системного анализа, теоретических основ информатики, дискретной математики, теории оптимизации, методика создания прикладных интеллектуальных систем.
В основу исследования положена гипотеза: если разработать концептуальные основы графового моделирования структур решений задач оптимизации и реализовать их в виде программных продуктов, то это даст возможность активизировать математическую деятельность изучающих теоретические основы информатики и дискретную математику, повысит качество и результативность решения прикладных задач в экономическом и сетевом планировании.
Научная новизна и теоретическая значимость исследования состоит в том, что в нем:
1.Выявлены структурные элементы решения задачи;
2.Выявлены отношения, связывающие эти структурные элементы;
3.Построены семантические графы первого порядка сложности, моделирующие эти отношения;
4.Дана количественная характеристика сложности решения задач;
5.Выявлены и систематизированы структуры решений задач оптимизации по числовой характеристике - сложности решения;
6.Разработана технология организации работы с программными средствами при решении задач с применением графовых моделей.
Первой работой теории графов как математической дисциплины считают статью Эйлера (1736 г.), в которой рассматривалась задача о Кёнингсбергских мостах. Эйлер показал, что нельзя обойти семь городских мостов и вернуться в исходную точку, пройдя по каждому мосту ровно один раз. Следующий импульс теория графов получила спустя почти 100 лет с развитием исследований по электрическим сетям, кристаллографии, органической химии и другим наукам.
Определение. Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Любое ребро связано не более чем с двумя вершинами.
Неформально граф можно рассматривать как множество точек и соединяющих эти точки линий со стрелками или без них.
С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема линий метрополитена. Точками на ней представлены станции, а линиями — пути движения поездов. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое древо. И это древо — граф.
Определение. Деревом называется связный граф без циклов. Очень важное понятие для подхода изложения теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания.
Графы служат удобным средством описания связей между объектами. Ранее мы уже использовали графы как способ наглядного представления конечных бинарных отношений.
Имеется две основные разновидности графов: неориентированные и ориентированные. Неориентированный граф – совокупность точек (вершин графа) с соединяющими некоторые из них отрезками (ребрами графа; ветвями). Ориентированный граф – это совокупность точек (вершин) с соединяющими некоторые из них ориентированными отрезками (стрелками). В этой работе мы будем пользоваться только ориентированными графами.
При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др., где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов). Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются линией или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Иногда рядом с ребром размещают поясняющие надписи, раскрывающие смысл ребра, например, в графах переходов конечных автоматов. Различают планарные и непланарные графы. Планарный граф — это граф, который можно изобразить на рисунке (плоскости) без пересечения рёбер (простейшие — треугольник или пара связанных вершин), иначе граф непланарный. В том случае, если граф не содержит циклов (содержащих, по крайней мере, один путь однократного обхода рёбер и вершин с возвратом в исходную вершину), его принято называть «деревом». Важные виды деревьев в теории графов — бинарные деревья, где каждая вершина имеет одно входящее ребро и ровно два выходящих, или является конечной — не имеющей выходящих рёбер и содержит одну корневую вершину, в которую нет входящего ребра.
Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.
Но граф используют отнюдь не только как иллюстрацию. Например, рассматривая граф, изображающий сеть дорог между населенными пунктами, можно определить маршрут проезда от пункта А до пункта Б. Если таких маршрутов окажется несколько, хотелось бы выбрать в определенном смысле оптимальный, например самый короткий или самый безопасный. Для решения задачи выбора требуется проводить определенные вычисления над графами. При решении подобных задач удобно использовать алгебраическую технику, да и само понятие графа необходимо формализовать.
Методы теории графов широко применяются в дискретной математике. Без них невозможно обойтись при анализе и синтезе различных дискретных преобразователей: функциональных блоков компьютеров, комплексов программ и т.д.
Вероятностный граф.
Определение. Граф называется вероятностным, если рядом с каждым его ребром записать соответствующую вероятность.
Это общий термин для обозначения вероятностного распределения графов. Вероятностные графы можно описать просто распределением вероятности или случайным процессом, создающим эти графы. Теория случайных графов находится на стыке теории графов и теории вероятностей. С математической точки зрения случайные графы необходимы для ответа на вопрос о свойствах типичных графов. Вероятностные графы нашли практическое применение во всех областях, где нужно смоделировать сложные сети — известно большое число случайных моделей графов, отражающих разнообразные типы сложных сетей в различных областях. В математическом контексте термин случайный граф означает почти всегда модель случайных графов Эрдёш — Реньи.
Правило вычисления вероятности по размеченному вероятностному графу:
1) вероятность попадания в конечную вершину (вероятность исхода) можно вычислить, перемножая вероятности, встречаемые на ребрах соответствующего маршрута (рис. 1.1, жирный маршрут);
P(A)=p1*q3*r2

Рис. 1.1 Вероятность попадания в одну конечную вершину
2) если же нас интересует вероятность события, которому благоприятствуют несколько исходов, то вероятности соответствующих конечных вершин складываются (рис.1.2, жирные маршруты).
P(B)=p1*q2+p2*r1

Рис. 1.2 Вероятность попадания в несколько вершин
Пример. В каждой из трех групп по 25 студентов. Число студентов группы, сдавших экзамен по математике, равно 22, 20 и 18 соответственно. Какова вероятность, что случайно выбранный студент сдал экзамен по математике?
Решение: Построим размеченный вероятностный граф (рис. 1.3):

Рис. 1.3 Вероятность сдачи экзамена студентами разных групп
Обозначим через A событие, заключающееся в том, что случайно выбранный студент сдал экзамен. Этому событию на графе благоприятствуют три маршрута. Поэтому:
P(A)=  *
*  +
+  *
*  +
+  *
*  =
=  =
= 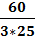 =
= 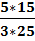 =
= 
Пример. Студент пришел на экзамен, зная 25 из 30 билетов. Какова вероятность того, что он сдаст экзамен, если после отказа отвечать на билет ему предоставляется возможность вытянуть еще один?
Решение: Построим размеченный вероятностный граф (рис. 1.4):

Рис. 1.4 Вероятность сдачи экзамена студентом
Обозначим через A событие, состоящее в том, что студент сдал экзамен. На графе вероятностей этому событию благоприятствуют два маршрута. Следовательно:
P(A)=  +
+  *
*  =
=  (1+
(1+  )=
)=  *
*  =
= 
Пример. В первой урне находятся 7 белых и 9 черных шаров, во второй - 6 белых и 4 черных шаров. Из первой урны во вторую переложили два шара, а затем из второй урны извлекли один шар. Найти вероятность того, что этот шар белый.
Решение: Построим размеченный вероятностный граф (рис. 1.5):

Рис. 1.5 Вероятность вынуть белый шар
Пусть событие A - извлеченный из второй урны шар оказался белым. Этому событию на графе благоприятствуют четыре маршрута. Поэтому:
P(A)=  *
* 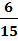 *
* 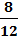 +
+  *
*  *
*  +
+  *
*  *
*  +
+  *
* 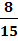 *
*  *
*  =
= 