Геометрическая вероятность

Лекция 1.

Теория вероятностей – это дисциплина, которая изучает закономерности случайных событий. Элементы случайности присутствуют и в природе (будет ясный день или облачный) и в технике (выход из строя мобильника) и в экономике (прибыльный или убыточный месяц). Для наглядности обычно используют монету, карты, кости, стрельбу по мишени. Основные понятия ТВ: опыт, событие, элементарный исход (случай).

Под опытом понимается выполнение определенного комплекса условий. При этом предполагается, что опыт может быть повторен сколько угодно раз. Для примера рассмотрим игру в кости. Опыт – бросок кубика. Комплекс условий – наличие кубика и игроков. Данные условия можно повторить много раз.

Событием называется всякий факт, который в результате опыта может произойти или не произойти. В прошлом примере опыт – бросание игрального кубика. События: A:(выпадение четного числа), B:(выпадение пятерки).

Элементарным исходом (случаем) называется один из взаимоисключаю­щих друг друга вариантов, которым может завершиться опыт. В примере с игрой в кости элементарными исходами являются выпадение единицы, двойки и т.д.

Как видно из примера, событие ­может включать в себе несколько элементарных исходов опыта. Связь между исходом и событием – это как отношение общего к частному. Например, A:(выпадение четного числа) состоит из элементарных исходов: выпадение двойки, четверки и шестерки. С другой стороны событие B:(выпадение шестерки) – состоит из одного элементарного исхода.

События бывают:

а) совместными – когда возникновение одного из событий не влияет на возникновение другого.Например, идет дождь и светит солнце, человек ест и смотрит телевизор одновременно, число целое и четное;

б) несовместными – если наступление одного из них исключает наступление другого. Например, день и ночь, человек читает и человек спит, число иррациональное и четное.

в) противоположными – если в данном испытании события несовместны и одно из них обязательно происходит. Например, если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.

г) независимыми – на возникновение этих событий не влияет возникновение других событий. Например, число, выпавшее на грани кубика, никак не зависит от предыдущего броска. Выпадение цифры никак не зависит от выпадения герба на предыдущем броске.

д) зависимыми – возникновение этих событий может произойти только при условии возникновения других событий, с которыми они связаны. Например, вытягивание второй и последующих карт из колоды, если при вытаскивании карты в колоду не возвращаются.

е) равновозможными – если по условиям симметрии событий нет оснований считать какое-либо из них более возможным, чем любое другое.

Полной группой событий называется несколько событий, таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Сумма вероятностей всех событий, составляющих полную группу, равна единице. Например, при сдаче зачета возможны следующие исходы: «зачтено», «не зачтено»; при подбрасывании монеты – «герб», «цифра»; при подбрасывании игральной кости – 1, 2, 3, 4, 5, 6. Эти события образуют полную группу.

Если несколько событий: 1) образуют полную группу; 2) несовместны; 3) равновозможны, то они называются случаями («шансами»).

Случай называется благоприятным событию, если появление этого случая влечет за собой появление события.

Классическое определение вероятности: Если результаты опыта сводятся к схеме случаев, то вероят­ность события А вычисляется как отношение числа т благоприятствующих событию А равновозможных исходов к общему числу всех исходов п, т.е. P(А)= m / n. Классическое определение вероятности не является пригодным, если результаты испытания не равновозможные.

Достоверным называется событие, которое в результате опыта непременно должно произойти. Р (А) = 1.

Невозможным называется событие, которое в результате опыта не может произойти. Р (А) = 0.

Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков.

Случайным называется событие, которое событие, которое может либо произойти, либо не произойти. Вероятность случайного событиязаключена между нулем и еди­ницей.

Вероятность противоположного события: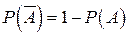

Пример 1. Из урны, содержащей 6 белых и 4 черных шара, наудачу вынут шар. Найти вероятность того, что он белый.

Решение. Число возможных исходов равно 10, а число исходов, благоприятных исходов – 6. Значит, 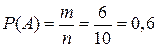. Противоположное событие (вытащить черный шар): .

Пример 2. Игра в русскую рулетку. Револьвер с шестизарядным барабаном в котором две пули. Найти вероятность выстрела при втором спуске крючка, если при первом спуске выстрела не было. Рассмотреть два различных способа расположенияы патронов в барабане?

Решение:

Вероятность выстрела при первом спуске вычисляется по общим законам математической статистики: .

Если барабан не вращается рукой после каждого спуска курка, то вероятности выстрела при втором спуске:

A) Если патроны находятся в двух подряд гнездах (4 подряд пустых гнезда) и первый выстрел попал на пустое гнездо, то следующее за ним гнездо в 3 случаях – пустое, в одном – заряженное. Поэтому в таком случае вероятность получить пулю при втором выстреле ¼.

В) Если патроны сидят в двух противоположных гнездах (через 2) и первый выстрел также попал на пустое гнездо, то следующее за ним гнездо либо пустое либо заряженное. Поэтому в таком случае вероятность получить пулю при втором выстреле 1/2.

Самое интересное, что информация о расположении ничего не значит при первом выстреле, но довольно много значит при втором.

Геометрическая вероятность

Если между всеми случаями опыта и площадью фигуры S можно установить взаимно-однозначное соответствие, а также можно установить взаимно-однозначное соответствие между случаями, благоприятствующими событию А, и площадью фигуры s, являющейся частью фигуры S, то вероятность события А через площади находим как .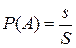

Пример 3. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата; б) правильного треугольника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.

Решение: Площадь круга равную 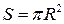можно рассматривать как все возможные значения точки, брошенной наугад. а)благоприятный исход попадания в квадрат, вписанный в круг, соответствует площади этого квадрата. Пусть квадрат имеет сторону а, тогда по теореме Пифагора диагональ квадрата будет равна 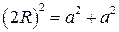или 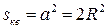, т.е. 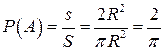. б)благоприятный исход попадания в правильный треугольник, вписанный в круг, соответствует площади этого треугольника. Пусть правильный треугольник имеет сторону а, тогда , .

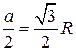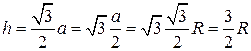, т.е. .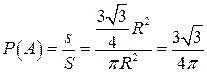

Подсчёт вероятности в классической схеме сводится к подсчёту общего числа «шансов» и числа шансов, благоприятствующих какому-либо событию. Число шансов считают с помощью формул комбинаторики.

Комбинаторика

В более сложных задачах для вычисления всех возможных случаев используются формулы комбинаторики. Например, сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?

Теорема 1: если первый элемент можно выбрать k способами, а второй элемент – m способами, то пару элементов можно выбрать k х m способами.

В этой задаче k =5; m =3. Ответ:15.

Пример 4. На завтрак в буфете можно выбрать: плюшку, бутерброд, пряник или кекс, а запить можно: кофе, соком, кефиром. Сколько возможных вариантов завтрака? В этой задаче k =4; m =3. Ответ:12.

Пример 5. Есть урна (ящик), содержащая n пронумерованных объектов (шаров). Мы выбираем из этой урны k шаров; результатом выбора является набор из k шаров. Нас интересует, сколькими способами можно выбрать k шаров из n, или сколько различных результатов может получиться. На этот вопрос нельзя дать однозначный ответ, пока мы не определимся:

– как организован выбор (можно ли шары возвращать в урну),

– что понимается под различными результатами выбора.

Рассмотрим следующие возможные способы выбора.

1. Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из k номеров шаров могут встречаться одни и те же номера.

2. Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.

Теперь условимся, какие результаты выбора (наборы из номеров шаров) мы будем считать различными. Есть ровно две возможности.

1. Выбор с учётом порядка (размещение) два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, при выборе двух шаров из урны, содержащей 5 шаров, наборы (1, 5), (5, 1) различны, если порядок учитывается.

2. Выбор без учёта порядка (сочетание) два набора номеров шаров считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми.

Так, наборы (5, 2) и (2, 5) не различаются и образуют один и тот же результат выбора, если порядок не учитывается.

Перечислим все возможные результаты выбора с различными возможностями и формулы для подсчета числа шансов в каждом из этих случаев.

без возвращения	с возвращением
с учётом порядка	без учёта порядка	с учётом порядка	без учёта порядка
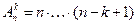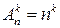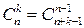