Свойства матрицы
- Сложение и вычитание допускается только для матриц одинакового размера.
- Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть: A + Θ = A
- Все элементы нулевой матрицы равны нулю.
- Возводить в степень можно только квадратные матрицы.
- Ассоциативность сложения: A + (B + C) = (A + B) + C.
- Коммутативность сложения: A + B = B + A.
- Ассоциативность умножения: A(BC) = (AB)C.
- Вообще говоря, умножение матриц некоммутативно:. Используя это свойство, вводят коммутатор матриц.
- Дистрибутивность умножения относительно сложения:
A(B + C) = AB + AC;
(B + C)A = BA + CA.
- С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
- Свойства операции транспонирования матриц:
(A T) T = A
(AB) T = B T A T
(A − 1) T = (A T) − 1, если обратная матрица A - 1 существует.
(A + B) T = A T + B T
detA = detA T
Элементарными преобразованиями матрицы называются преобразования следующих трёх типов:
1. Перестановка двух строк (столбцов) матрицы; транспорирование
2. Умножение строки (столбца) на число отличное от нуля;
3. Прибавление к одной строке (столбцу) матрицы другой её строки (столбца), умноженной на любое число
4. Отбрасывание нулевой строки.
Транспонирование
Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. A = (a ij), то A T = (a ji).
Минор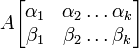 
матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами 
и столбцов с номерами 
.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимойподсистемой системы всех строк (столбцов) матрицы.
Пример
Например, есть матрица:
Предположим, надо найти дополнительный минор 
. Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:
Получаем 
Обратная матрица
Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
AA -1 = A -1 A = E
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
C * (союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
Ранг матрицы
Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.
Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы. Ранг матрицы не изменяется при элементарных преобразованиях.(см. свойства матрицы) С помощью элементарных преобразований матрицу приводят к ступенчатому виду, число ненулевых строк указывает на ранг матрицы. Ранг матрицы не превышает кол-во столбцов
Линейная комбинация строк/столбцов матрицы
Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).В противном случае строки (столбцы) называются линейно независимыми.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевымопределителем основной матрицы (причём для таких уравнений решение существует и единственно)
Система линейных уравнений:
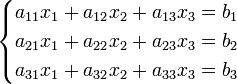
Определители:
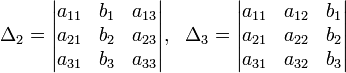
Решение:
