Анализируя вышеизложенное, можно сделать вывод, что дифференциальные уравнения представляют собой модель целого класса, целой совокупности явлений, процессов. Анализ их и в частности, интегрирование дает большое количество решений, удовлетворяющих исходному дифференциальному уравнению. Исследователь же имеет конкретную задачу. Поэтому, для получения из множества возможных решений одного, удовлетворяющего только рассматриваемому процессу (объекту исследования) задаются дополнительные условия. Таким образом, должен быть определенно выделен исследуемый процесс из всего класса, в который он входит.
Условия, раскрывающие все особенности выбранного уравнения, называются условиями однозначности. Условия однозначности характеризуются следующими свойствами и признаками: параметрами и режимами объекта (основными параметрами и режимами рабочего органа, например, подача и напор струи при вскрыше, и удаление породы при открытом способе добычи каменного угля и других полезных ископаемых); физическими свойствами исследуемого объекта (влажность, твердость, структура, плотность породы и др.); начальными условиями, характеризуемыми состоянием исследуемого объекта в начальный момент (скорость движения семени при сходе с распределителя при изучении траектории его в подлаповом пространстве сошника сеялки, скорость снежно-воздушного потока перед преградой при изучении отложения снега за преградой и др.); граничными условиями, описываемыми пределами взаимодействия изучаемой системы на границах с окружающей средой (например, при оптимизации параметров сошниковых систем граничными условиями являются предельные размеры их по длине, которые не должны превышать базовые размеры рамы, определяемые конструктором заводского конвейера производства сеялок и др.). В процессе обоснования основных параметров и режимов функционирования исследуемого объекта начальные и граничные условия называют краевыми условиями оптимизации.
В качестве примера производится несложное исследование, в котором, не смотря не его простоту, содержатся почти все вышеизложенные элементы научного исследования с применением математического аппарата в классе дифференциальных уравнений.
Исследование связано с созданием сеялки для внутрипочвенного – разбросного посева зерновых культур, в условиях дефицита почвенной влаги и подверженности почвы ветровой эрозии.
Итак, существует проблема повышения урожайности зерновых
культур путем улучшения равномерности распределения семян по площади питания и глубине заделки в почву.
Создалась проблемная ситуация в виде противоречивых позиций при решении этой проблемы.
Одним из основных недостатков современного рядкового посева является сосредоточение семян в рядке и отсутствие их в междурядье (в соответствии с пословицей “где густо, а где пусто”), в связи с чем, неравномерно, а потому и не полностью используется растениями площадь питания (поля).
Следовательно, чтобы равномернее распределить семена по площади питания, необходимо увеличить расстояние между ними в рядке и уменьшить – в междурядье. А для этого необходимо уменьшить расстояние между дисковыми сошниками, формирующими рядки, что противоречит условиям незабиваемости их почвой и растительными остатками в ней. Необходимо разделение этой противоречивой ситуации путем создания необходимой адекватной теории, из условий которой можно создать средства механизации, обеспечивающие равномерное распределение семян в почве и незабиваемость почвой.
Была выдвинута гипотеза, заключающаяся в том, что решение этой проблемы можно осуществить путем использования рабочего органа в виде культиваторной лапы, в подлаповом пространстве которой можно, равномерно распределять семена по всей ширине захвата.
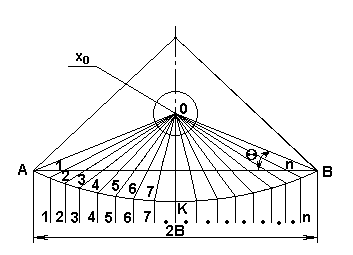
Рассматривая подлаповое пространство в плане в виде суммы элементарных секторов 1, 2, 3…n, а ширину захвата в виде суммы элементарных полосок, 1,2,3…n, число которых достаточно велико, распределение семян можно считать удовлетворительным, если в каждой продольной полоске будет находиться одинаковое количество семян (рисунок 3.6.).
Рисунок 3.6 - Схема рабочего органа в плане.
А это возможно, если будет выполняться условие:
L 
, (3.9)
где L - дальность полета семян от распределителя;
Q - угол ограничительной плоскости полета семян;
2B - ширина захвата сошников, удовлетворяющая условию незабиваемости их.
Принимая зерна за материальную точку и пренебрегая сопротивлением воздуха (Jз » 1,5…1,7 м/с, допускаемая ошибка при этом 0,6…0,7 %), дифференциальное уравнение движения их запишутся в виде (рисунок 3.7):
, 
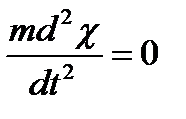, (3.10)
где m - масса зерна.
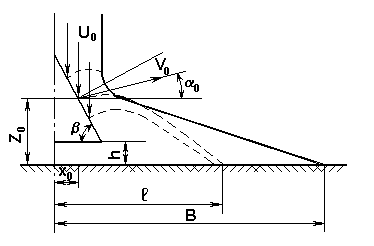
После двойного интегрирования этих уравнений при начальных условиях движения и, исключив из уравнения параметр t, получим уравнение траектории движения зерна после схода с поверхности распределителя:
Рисунок 3.7 - Схема работы внутрипочвенно-разбросного сошника в перечно-вертикальной плоскости.
, (3.11)
где V0 - начальная скорость движения зерна после схода с распределителя;
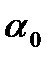- угол направления начальной скорости;
Z0 - высота установки распределителя;
X0 - радиус основания распределителя.
Полученное выражение (3.10) представляет собой модель распределения семян в общем виде.
Это дает возможность дальнейшего анализа и обоснования основных параметров распределителя. Проведем несложный анализ на предмет поставленной ранее задачи. Модель (3.10) описывает траекторию полета зерновок. Параметры этой траектории (Z) могут принимать самые разные значения, но нам нужно получить такую траекторию, двигаясь по которой, зерно не ударялось бы о свод подлапового пространства. Наибольшую дальность полета обеспечит траектория, которая касается свода без импульса силы зерновки с его стороны. Только в этом случае дальность полета приобретает заданное значение.
Абсцисс точки пересечения траектории полета семян с дном борозды представляет собой дальность их полета, которая определяется из (3.10), приняв Z = 0 (на уровне борозды Z = 0):
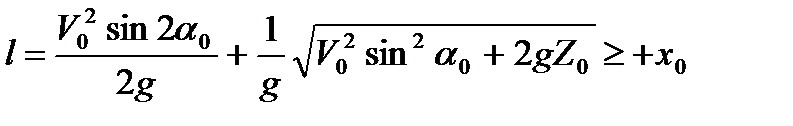. (3.12)
С учетом (3.11) условие удовлетворительной дальности полета семян запишется в виде:
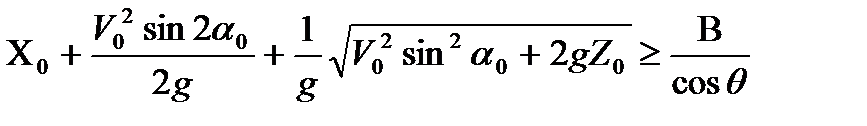. (3.13)
В самом неблагоприятном положении, в связи с этим, находятся семена летящие в вертикальной плоскости, проходящей через центр 0 распределителя и задний конец лезвия лапы сошника, так как секущая этой плоскости имеет наименьший угол наклона ко дну борозды, что и обусловливает в этом месте самый низкий свод.
Следовательно, полет зерна без удара о свод в подсошниковом пространстве, а следовательно, и равномерное распределение семян по площади питания, будет при условии:
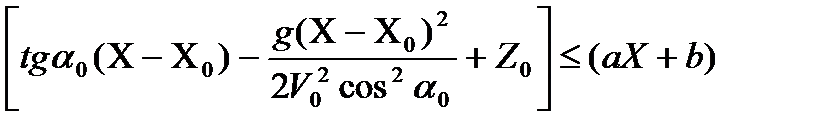, (3.14)
где Z = ax + b - уравнение свода в плоскости с худшими условиями для полета зерна.
Довольно подробно рассмотренный пример формирования математической модели объекта с помощью математического аппарата в форме дифференциальных уравнений, и ее анализ наглядно показывает преимущество такого метода исследования и возможности анализа на предмет обоснования конкретных, интересуемых исследователя параметров.