Сущность метода заключается в следующем.
Пусть необходимо найти корень уравнения 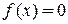 с заданной точностью ε.
с заданной точностью ε.
Исходное уравнение 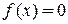 заменим равносильным ему уравнением
заменим равносильным ему уравнением  . Это можно сделать различными способами. Например, выделить из исходного уравнения
. Это можно сделать различными способами. Например, выделить из исходного уравнения 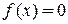 переменную x, остальное перенести в правую часть. Правая часть и составит выражение для
переменную x, остальное перенести в правую часть. Правая часть и составит выражение для  .
.
Выберем на отрезке [ a, b ] произвольное значение x 0 в качестве нулевого приближения для искомого корня. Подставляя это значение в правую часть уравнения 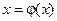 , получим уточненное значение x 1 искомого корня
, получим уточненное значение x 1 искомого корня  . Снова подставляя полученное значение x 1 в правую часть уравнения
. Снова подставляя полученное значение x 1 в правую часть уравнения  , получим значение x 2 искомого корня в следующем приближении
, получим значение x 2 искомого корня в следующем приближении  . Продолжая этот процесс, получим последовательность приближений:
. Продолжая этот процесс, получим последовательность приближений:  ,
, 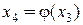 , …
, …  . Эту последовательность называют итерационной.
. Эту последовательность называют итерационной.
Установлено, если существует предел последовательности x 0, x 1, x 2, …, xn, т. е.  , то он является корнем ξ уравнения
, то он является корнем ξ уравнения 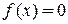 и может быть вычислен по формуле
и может быть вычислен по формуле  с любой степенью точности ε.
с любой степенью точности ε.
Рассмотрим геометрическую интерпретацию метода итерации. Построим в плоскости x 0 y график  левой части уравнения
левой части уравнения  . Это будет биссектриса координатного угла (рис. 2, а). Затем строим график правой части уравнения
. Это будет биссектриса координатного угла (рис. 2, а). Затем строим график правой части уравнения  , т. е. график
, т. е. график  . Получим некоторую линию L на плоскости x 0 y.
. Получим некоторую линию L на плоскости x 0 y.
Пусть для любой точки этой линии на интервале [ a, b ] соблюдается условие 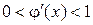 . Абсцисса ξ точки пересечения линии L с биссектрисой
. Абсцисса ξ точки пересечения линии L с биссектрисой  является корнем уравнения
является корнем уравнения 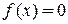 (таких точек в общем случае может быть несколько). Найдем значение ξ корня.
(таких точек в общем случае может быть несколько). Найдем значение ξ корня.
Зададимся в качестве приближенного значения корня величиной 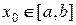 . Согласно методу итерации, новое приближение для искомого корня ξ будет
. Согласно методу итерации, новое приближение для искомого корня ξ будет  . Геометрически x 1 находим, проведя через точку A 0 кривой L прямую, параллельную оси абсцисс, до пересечения с прямой
. Геометрически x 1 находим, проведя через точку A 0 кривой L прямую, параллельную оси абсцисс, до пересечения с прямой  . Абсцисса точки B 1 пересечения и дает x 1 (рис. 2, а). Продолжая этот процесс, получим точки x 2, x 3, …. Последовательность этих значений стремится к значению ξ искомого корня уравнения
. Абсцисса точки B 1 пересечения и дает x 1 (рис. 2, а). Продолжая этот процесс, получим точки x 2, x 3, …. Последовательность этих значений стремится к значению ξ искомого корня уравнения 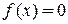 .
.
Возможен случай, когда для кривой L графика  выполняется условие
выполняется условие  (рис. 2, б). Последовательные вычисления приближенных значений корня, как на рис. 2, а, показаны стрелками. Приближения x 1, x 2, … здесь также сходятся к искомому решению ξ. Однако в отличие от предыдущего случая, где решение уравнения представляет собой вид «лестницы», здесь решение имеет вид «спирали».
(рис. 2, б). Последовательные вычисления приближенных значений корня, как на рис. 2, а, показаны стрелками. Приближения x 1, x 2, … здесь также сходятся к искомому решению ξ. Однако в отличие от предыдущего случая, где решение уравнения представляет собой вид «лестницы», здесь решение имеет вид «спирали».
Геометрическое представление метода итерации для случаев, когда  и
и  (рис. 2, в, г) показывает, что в этих случаях метод итерации не обладает сходимостью, т. е. последовательное вычисление приближенных значений x 0, x 1, x 2, …, xn корня не приводит к искомому решению ξ.
(рис. 2, в, г) показывает, что в этих случаях метод итерации не обладает сходимостью, т. е. последовательное вычисление приближенных значений x 0, x 1, x 2, …, xn корня не приводит к искомому решению ξ.
 |
Таким образом, метод итерации обладает сходимостью тогда, когда
 и не обладает сходимостью при
и не обладает сходимостью при  . В соответствии с этим примем без доказательства следующую теорему.
. В соответствии с этим примем без доказательства следующую теорему.
Пусть функция  определена и дифференцируема на отрезке [ a, b ], причем все ее значения
определена и дифференцируема на отрезке [ a, b ], причем все ее значения 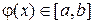 . Тогда, если существует правильная дробь q такая, что
. Тогда, если существует правильная дробь q такая, что  на отрезке [ a, b ], то:
на отрезке [ a, b ], то:
1) процесс итерации 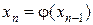 (n = 1, 2, …) сходится независимо от начального значения
(n = 1, 2, …) сходится независимо от начального значения 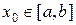 ;
;
2) предельное значение  является единственным корнем уравнения
является единственным корнем уравнения  , следовательно,
, следовательно,  на отрезке [ a, b ].
на отрезке [ a, b ].
За число q можно принять наименьшее значение модуля производной 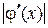 на отрезке [ a, b ]. При этом процесс итерации следует продолжать до тех пор, пока для двух последовательных приближений xn -1 и xn не будет выполнено неравенство
на отрезке [ a, b ]. При этом процесс итерации следует продолжать до тех пор, пока для двух последовательных приближений xn -1 и xn не будет выполнено неравенство
 ,
,
что обеспечивает выполнение условия 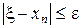 .
.
Если  , то уточнение корня можно вести до соблюдения неравенства
, то уточнение корня можно вести до соблюдения неравенства  .
.
На рис. 2, д приведена блок-схема алгоритма уточнения корня уравнения 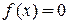 методом итерации. Исходными данными являются начальное приближение x 0 для искомого корня и точность ε, с которой необходимо вычислить корень уравнения.
методом итерации. Исходными данными являются начальное приближение x 0 для искомого корня и точность ε, с которой необходимо вычислить корень уравнения.
Блок 3 задает начальное приближение для корня x. Блоки 4-6 составляют цикл уточнения корня по формуле 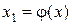 , где x и x 1 – предыдущее и последующее приближение соответственно.
, где x и x 1 – предыдущее и последующее приближение соответственно.
Отметим общую методику уточнения корня методом итерации.
1) исходное уравнение 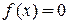 заменить равносильным уравнением
заменить равносильным уравнением  ;
;
2) исследовать уравнение  на сходимость процесса итерации, т. е. определить
на сходимость процесса итерации, т. е. определить 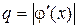 ;
;
3) если  , произвести уточнение корня до заданной точности ε по формуле
, произвести уточнение корня до заданной точности ε по формуле  . Если
. Если 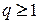 , подобрать другое уравнение
, подобрать другое уравнение  и повторить п. 2.
и повторить п. 2.
Пример. Дано нелинейное уравнение
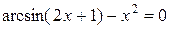 (1)
(1)
и интервал существования его корня 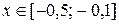 . Вычислить методом итерации значение корня с точностью ε = 0,001.
. Вычислить методом итерации значение корня с точностью ε = 0,001.
Решение. Согласно методу итераций исходное уравнение следует привести к виду  . Это можно сделать несколькими способами, например:
. Это можно сделать несколькими способами, например:
Первый способ. Исходное уравнение  запишем в виде
запишем в виде  , отсюда
, отсюда 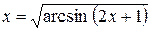 , т.е.
, т.е.
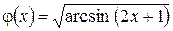 ; (2)
; (2)
Второй способ. Как и в первом способе, исходное уравнение приведем к виду  . Возьмем от обеих частей синус
. Возьмем от обеих частей синус
 .
.
Так как  , то
, то 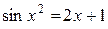 . Отсюда
. Отсюда 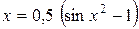 , т. е
, т. е
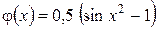 . (3)
. (3)
Проверим, какая из полученных функций 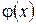 обеспечивает сходимость метода итераций, т.е. удовлетворяет требованию
обеспечивает сходимость метода итераций, т.е. удовлетворяет требованию  на интервале
на интервале  существования корня.
существования корня.
Для функции (2) при подстановке значений  получим
получим
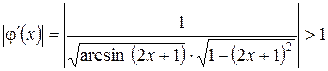 .
.
Для функции (3) при подстановке значений  получим
получим
 .
.
Поскольку, условию сходимости процесса итераций удовлетворяет функция  , то уточнение корня будем производить по формуле
, то уточнение корня будем производить по формуле 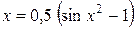 .
.
Таким образом, исходная математическая задача определения корня уравнения сводится к следующей вычислительной задаче:
вычислять по формуле 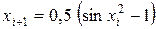 ,
,  значение корня уравнения
значение корня уравнения 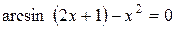 до выполнения условия
до выполнения условия 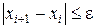 .
.
За начальное приближение  искомого корня принимаем любую точку из
искомого корня принимаем любую точку из 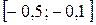 , например
, например 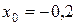 .
.
Приведём результаты вычислений первых двух приближений  и
и  для уточняемого корня:
для уточняемого корня:
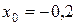 ;
;
 .
.
В первом приближении  . Так как
. Так как  , то, принимая
, то, принимая  , производим вычисление корня в следующем (втором) приближении (начиная с блока 3):
, производим вычисление корня в следующем (втором) приближении (начиная с блока 3):
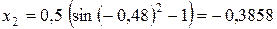 .
.
Таким образом, имеем 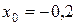 ;
;  ;
; 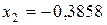 . Заметим, что
. Заметим, что  , поэтому процесс уточнения корня должен быть продолжен.
, поэтому процесс уточнения корня должен быть продолжен.
Из приведенных выше примеров преобразования исходного уравнения 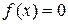 к виду
к виду  можно заметить, что от вида функции
можно заметить, что от вида функции  уравнения
уравнения  зависит сходимость метода итераций. Поэтому обычно применяют общий прием построения функции
зависит сходимость метода итераций. Поэтому обычно применяют общий прием построения функции  , для которой обеспечивается выполнение условия сходимости
, для которой обеспечивается выполнение условия сходимости  на отрезке [ a, b ].
на отрезке [ a, b ].
Исходное уравнение  умножают на произвольную константу λ и прибавляют к обеим частям полученного уравнения
умножают на произвольную константу λ и прибавляют к обеим частям полученного уравнения 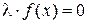 переменную x, т. е. представляют
переменную x, т. е. представляют  в виде
в виде  , где
, где 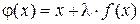 .
.
При этом предполагается, что на отрезке [ a, b ] производная 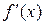 существует и сохраняет свой знак. Кроме того, имеет место неравенство:
существует и сохраняет свой знак. Кроме того, имеет место неравенство:
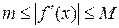 , где
, где  ;
;  .
.
Значение константы λ выбирается таким, чтобы в интервале [ a, b ] существования корня ξ выполнялось неравенство
 ,
,
которое можно записать в виде
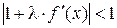 .
.
Из последнего имеем: 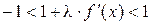 . Решением правого неравенства
. Решением правого неравенства  является
является
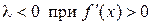 и
и  ,
,
а из левого неравенства 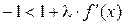 получим
получим
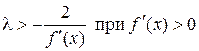 и
и 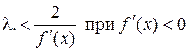 .
.
Таким образом, в зависимости от знака производной  имеем:
имеем:
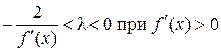 и
и 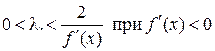 .
.
Учитывая, что 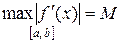 за значение константы λ принимают:
за значение константы λ принимают:
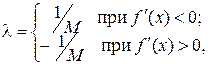
при котором условие 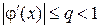 сходимости процесса уточнения корня соблюдается.
сходимости процесса уточнения корня соблюдается.