Результаты решения задач и упражнений

Практическое занятие 1

Тема 2. Методы решения нелинейных уравнений

Лк –1,5 ч., ПЗ – 2 ч., СРС – 8 ч.).

 

 

Расчетное задание

1. Используя формулу Лагранжа, установить интервалы существования отрицательных и положительных корней алгебраического уравнения 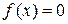. Уравнение 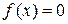выбрать из таблицы 1 согласно варианту задания.

2. Выполнить с помощью ЭВМ отделение всех корней заданного уравнения .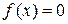

Таблица 1. Варианты уравнений

 

№ варианта	Уравнение	№ варианта	Уравнение

 

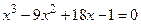
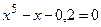
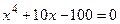
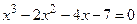
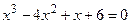
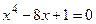
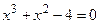
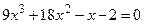
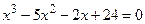
Методические указания к выполнению задания

 

1. Выберите из таблицы 1 уравнение 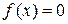. Определите верхние к нижние границы областей существования отрицательных и положительных корней уравнения.

2. Разработайте схему алгоритма отделения всех корней уравнения 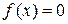. В качестве границ исходного интервала (a, b) отделения корней примите нижнюю границу отрицательных корней и верхнюю границу положительных корней. Шаг отделения корней вычислите по формуле , где n - число шагов (n =15…20).

3. Разработайте тест отладки программы отделения корней, приняв n = 3…4. Составьте таблицу промежуточных результатов теста.

4. С помощью табличного процессора Excel выполните отделение корней уравнения 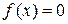. Предварительно, используя разработанный тест, проверьте правильность работы составленной программы, при необходимости выполните ее отладку.

 

Задачи и упражнения для самостоятельной работы

По приобретению умений и навыков по теме 2

 

1. Установите области определения уравнений:

; .

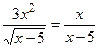Приведите к виду 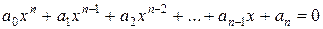эти уравнения.

2. Какова методика определения области корней трансцендентного уравнения? Определите область существования корней уравнения

 

.

 

3. Напишите в вербальной (словесной) форме последовательность отделения наибольшего корня уравнения , расположенного на интервале [0,25; 3,45].

4. Используя два способа, т. е. записывая нижеприведенное уравнение в виде 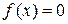в первом способе и как 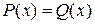- во втором, графическим методом выполните отделение корней уравнения . Длину отрезка расположения каждого корня задать равной 0,2.

 

Содержание отчета

- постановка задачи расчетного задания;

- определение границ областей существования отрицательных и положительных корней уравнения 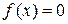с подробным описанием выполняемых операций;

- схема алгоритма отделения корней уравнения ;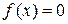

- тест отладки программы отделения корней;

- результаты решения задачи отделения корней, представленных в табличной форме;

- результаты выполнения упражнений;

- ответы на контрольные вопросы темы 2.

 

Пример оформления отчета

 

Тема 2. Методы решения нелинейных уравнений

 

Расчетное задание

1. Используя формулу Лагранжа, установить интервалы существования отрицательных и положительных корней алгебраического уравнения

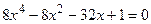. (1)

2. Выполнить с помощью ЭВМ отделение наибольшего положительного корня уравнения (1).

 

Решение задания по п. 1. Найдем верхнюю границу 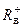области существования положительных корней существования положительных корней уравнения (1). В этом уравнении: a _{0 =} 8, a ₁ = 0, a ₂ = -8, a ₃ = -32, a ₄ = 1. Номер первого из отрицательных коэффициентов k = 2. Наибольший по абсолютному значению из отрицательных коэффициентов полинома f (x) B = 32. Тогда по формуле Лагранжа получаем

.

Для определения нижней границы положительных корней заданного уравнения (1) строим вспомогательное уравнение

 

или .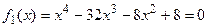

Для него имеем: a _{0 =} 1, a ₁ = -32, a ₂ = -8, a ₃ = 0, a ₄ = 8, k = 1 и B = 32. То-есть, для вспомогательного уравнения 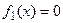верхней границей его положительных корней является R ₁ = 1+32 = 33. Следовательно, для уравнения (1) имеем .

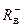Для определения границ и области отрицательных корней уравнения (1) строим два вспомогательных уравнения

;

.

Для первого из них имеем: a _{0 =} 1, a ₁ = 32, a ₂ = -8, a ₃ = 0, a ₄ = 8, k = 2 и B = 8. Следовательно, для вспомогательного уравнения 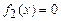верхней границей его положительных корней будет

.

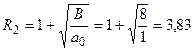Для уравнения имеем: a _{0 =} 8, a ₁ = 0, a ₂ = -8, a ₃ = 32, a ₄ = 1, k = 2 и B = 8. Следовательно, для него верхней границей его положительных корней будет

.

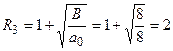Таким образом, если исходное уравнение 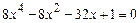имеет действительные корни, то они обязательно лежат в интервалах

.

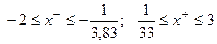Решение задания по п. 2. Согласно результатам выполнения задания по п. 1, положительные корни уравнения (1), если они есть, находятся в интервале .

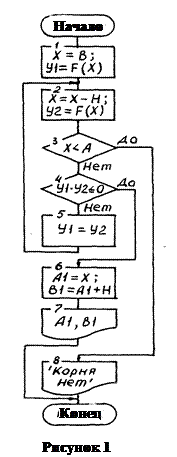Для краткости отображения алгоритма отделения наибольшего корня введены следующие обозначения (рисунок 1):

B = 3, A = 1/33 – верхняя и нижняя границы области существования положительных корней уравнения сооветственно;

x – значение границы (правой или левой) проверяемого текущего интервала;

H = 0,2 – шаг отделения корня;

F (x) – левая часть уравнения (1);

Y 1 и Y 2 – значения функции F (x) на правой и левой границах проверяемого текущего отрезка интервала существования положительных корней уравнения;

B 1, A 1 - правая и левая границы интервала существования наибольшего положительного корня уравнения.

Основу алгоритма составляет циклический процесс последовательного вычисления функции F (x) –уравнения (1) в точках интервала существования положительных корней, начиная с его правой границы. Искомым решением задачи отделения наибольшего корня является отрезок[ A 1; B 1], на концах которого будет обнаружено изменение знака функции F (x), т.е. выполнение условия .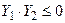

В таблице 2 приведены результаты реализации в Excel разработанного алгоритма.

Таблица 2. Результаты выполнения алгоритма отделения корня

 

A	B	x	Y 1	Y 2	Y 1* Y 2<0	A 1	B 1
0,03
H		2,8	340,4048	340,4048
0,2		2,6	229,3008	229,3008	ЛОЖЬ
		2,4	143,5408	143,5408	ЛОЖЬ
		2,2	79,2848	79,2848	ЛОЖЬ
					ЛОЖЬ
		1,8	1,4608	1,4608	ЛОЖЬ
		1,6		-18,2512	ИСТИНА	1,6	1,8

 

Результаты решения задач и упражнений

1. Установить область определения уравнения и привести его к виду .

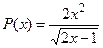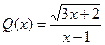Для данного уравнения имеем: и . Области определения этих функци й: 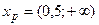, 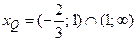. Следовательно, для уравнения область определения 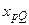составляет совокупность интервалов , так как она общая для и .

Для приведения к виду уравнения возведем обе его части в квадрат и после приведения к общему знаменателю, получим

.

 

2. Определить область существования корней уравнения .

Исходное уравнение запишем в виде , где функции ; 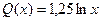. Область определения этих функций и область их значений составляют:

, ; , .

Так как , то корни исходного уравнения, если они есть, будут принадлежать общей области определения функций P (x) и Q (x), т. е. .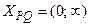

 

Ответы на контрольные вопросы

 

1. На какие два класса подразделяются все уравнения? Приведите примеры уравнений этих классов.

В зависимости от того, какие функции входят в уравнения, они разделяются на два больших класса: алгебраические уравнения и трансцендентные.

В алгебраические уравнения входят только алгебраические функции, при вычислении значений которых выполняются только арифметические операции и возведение в степень, например

, .

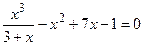Трансцендентным является уравнение, в состав которого входят одна или несколько таких функций как: показательная a^x, логарифмическая log _a x, тригонометрические sin x, tg x и др. Например, .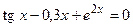

2. ….