Раздел 2. Элементы аналитической геометрии.
Тема 2.1. Векторы
Направленный отрезок (или упорядоченная пара точек) называется вектором.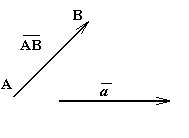 | Вектор обычно обозначается символом 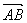 , где А – начало, а В – конец направленного отрезка, либо одной буквой , где А – начало, а В – конец направленного отрезка, либо одной буквой 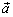 |
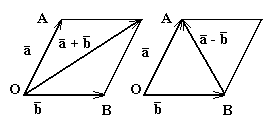 Рис 1.Сложение векторов Рис 1.Сложение векторов | Определение Суммой векторов 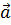 и и 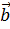 называется такой третий вектор называется такой третий вектор 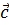 , что при совмещенных началах этих трех векторов, векторы , что при совмещенных началах этих трех векторов, векторы 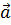 и и 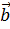 служат сторонами параллелограмма, а вектор служат сторонами параллелограмма, а вектор 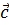 – его диагональю (рис.1). Сложение векторов в соответствии с рисунком называется сложением по правилу параллелограмма
Разностью векторов – его диагональю (рис.1). Сложение векторов в соответствии с рисунком называется сложением по правилу параллелограмма
Разностью векторов 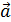 и и 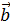 называется сумма называется сумма 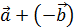 . . |
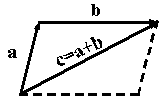 Рис2.Правило треугольника Рис2.Правило треугольника | Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 2. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы. |
 Рис.3Умножение вектора на число
Рис.3Умножение вектора на число
| Определение Произведением вектора 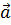 на вещественное число на вещественное число 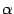 называется вектор называется вектор 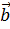 , определяемый условием 1) , определяемый условием 1) 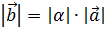 и, если и, если 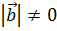 , то еще двумя условиями:
2) вектор , то еще двумя условиями:
2) вектор 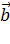 коллинеарен вектору коллинеарен вектору 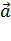 ;
3) векторы ;
3) векторы 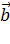 и и 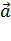 направлены одинаково, если α >0, и противоположно, если α<0.
Произведение вектора направлены одинаково, если α >0, и противоположно, если α<0.
Произведение вектора 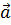 на число на число 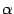 обозначается обозначается 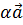 (рис 3). (рис 3).
|
Тема 2.2. Прямые. Кривые второго порядка.
§1. Прямая на плоскости. Различные виды уравнения прямой.
Каждая прямая на плоскости определяется линейным уравнением первой степени с двумя неизвестными.
1. Уравнение прямой с угловым коэффициентом:
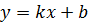 , где
, где
k – угловой коэффициент прямой (т. е. тангенс угла α, который прямая образует с положительным направлением оси OX, k=tgα), b – ордината точки пересечения прямой с осью OY.
2. Общее уравнение прямой:
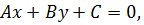 где
где
A, B и C – постоянные коэффициенты, причём A и В одновременно не обращаются в нуль (А2+В2≠0).
Частные случаи этого уравнения:
a. Ax+By=0 (C=0) – прямая проходит через начало координат;
b. Ax+C=0 (B=0) – прямая параллельна оси OY;
c. By+C=0 (A=0) – прямая параллельна оси OX;
d. Ax=0 (B=C=0) – прямая совпадает с осью OY;
e. By=0 (A=C=0) – прямая совпадает с осью OX.
3. Уравнение прямой в отрезках:
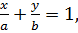 где
где
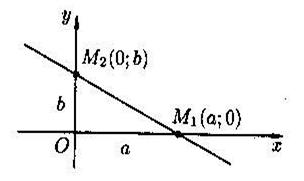 a и b – длины отрезков (с учётом знаков), отсекаемых прямой на осях OX и OY соответственно.
a и b – длины отрезков (с учётом знаков), отсекаемых прямой на осях OX и OY соответственно.
4. Уравнение прямой, проходящей через данную точку в данном направлении:
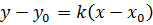 , где k =
, где k = 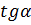 (
(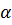 – угол, образуемый прямой с осью ОХ);
– угол, образуемый прямой с осью ОХ); 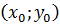 – координаты данной точки.
– координаты данной точки.
5. Уравнение прямой, проходящей через две данные точки М1(x1;y1) и М2(x2;y2), где y1≠y2, x1≠x2 имеет вид: 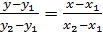 .
.
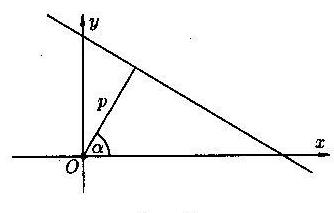
6. Нормальное уравнение прямой: 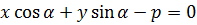 , где p – длина перпендикуляра, опущенного из начала координат на прямую,
, где p – длина перпендикуляра, опущенного из начала координат на прямую, 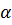 – угол, который этот перпендикуляр образует с положительным направлением оси ОХ
– угол, который этот перпендикуляр образует с положительным направлением оси ОХ
 |
Общее уравнение прямой можно преобразовать в нормальное путём умножения на нормирующий множитель 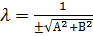 ; знак перед дробью берётся противоположным знаку свободного члена С (в общем уравнении прямой).
; знак перед дробью берётся противоположным знаку свободного члена С (в общем уравнении прямой).
Задание № 5 (пример). Уравнение 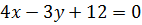 представить в различных видах (с угловым коэффициентом, в отрезках, в виде нормального уравнения).
представить в различных видах (с угловым коэффициентом, в отрезках, в виде нормального уравнения).
Решение. Для получения уравнения прямой с угловым коэффициентом решим заданное уравнение относительно y. Получим 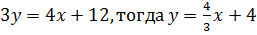 – уравнение прямой с угловым коэффициентом; здесь
– уравнение прямой с угловым коэффициентом; здесь 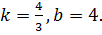
Для получения уравнения прямой в отрезках перенесём свободный член С=12 вправо и разделим обе части уравнения на ̶ 12. В результате получим: 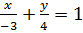 – уравнение в отрезках на осях; здесь а =
– уравнение в отрезках на осях; здесь а = 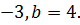
Приведём исходное уравнение к нормальному виду. Для этого умножим обе части уравнения 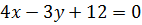 на нормирующий множитель
на нормирующий множитель 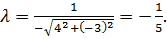 Перед корнем взят знак «минус», т. к. свободный член (С=12) имеет знак «плюс». Получим
Перед корнем взят знак «минус», т. к. свободный член (С=12) имеет знак «плюс». Получим 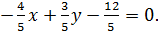 Здесь
Здесь 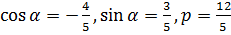 , т. е. расстояние от О(0;0) до прямой равно 2,4.
, т. е. расстояние от О(0;0) до прямой равно 2,4.
§2. Кривые второго порядка.
1. Окружностью называется множество всех точек плоскости, удалённых от заданной точки А на одно и тоже расстояние R. Точка A называется центром, а R – радиусом окружности.
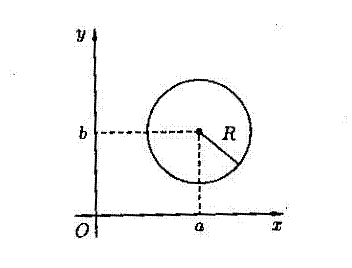
В прямоугольной системе координат уравнение окружности имеет вид 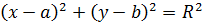 , где (a;b) – координаты её центра. Если a=0, b=0, то центр окружности совпадает с началом координат и уравнение окружности имеет вид
, где (a;b) – координаты её центра. Если a=0, b=0, то центр окружности совпадает с началом координат и уравнение окружности имеет вид 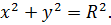
 |
2.
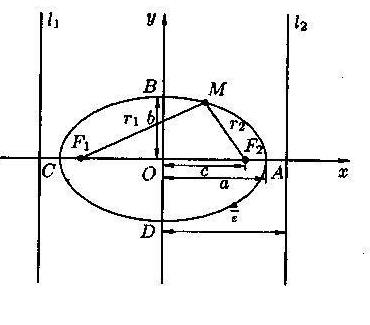 |
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Каноническое уравнение эллипса:
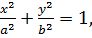 где a – большая полуось,b – малая полуось эллипса. Координаты фокусов: F1(̶ c;0); F2(с;0), где c – половина расстояния между фокусами. Числа a,b и c связанысоотношением
где a – большая полуось,b – малая полуось эллипса. Координаты фокусов: F1(̶ c;0); F2(с;0), где c – половина расстояния между фокусами. Числа a,b и c связанысоотношением 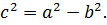 Точки A, B, C, D называют вершинами эллипса, точка О – центром эллипса, расстояния r1 и r2 от произвольной точки М эллипса до его фокусов называют фокальными радиусами этой точки.
Точки A, B, C, D называют вершинами эллипса, точка О – центром эллипса, расстояния r1 и r2 от произвольной точки М эллипса до его фокусов называют фокальными радиусами этой точки. Эксцентриситетом ε эллипса называется отношение фокусного расстояния 2с (расстояния между фокусами) к большой оси 2а:
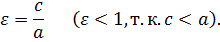
Фокальные радиусы определяются формулами:
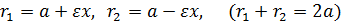 .
.Директрисами эллипса называются прямые l1 и l2 параллельные малой оси эллипса и отстоящие от неё на расстоянии, равном
 ; уравнения директрис:
; уравнения директрис: 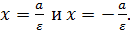
Замечания.
1) Если a=b, то каноническое уравнение эллипса определяет окружность 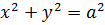 ;
;
2) если фокусы эллипса лежат на оси Oy, то эллипс имеет вид, изображенный на рисунке:
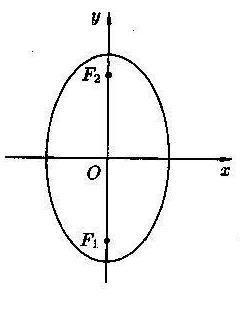 |
В этом случае:
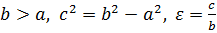 , уравнения директрис
, уравнения директрис 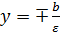 ;
;
3) уравнения эллипса с осями, параллельными координатным, имеет вид: 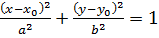 ; где (x0; y0) – координаты центра эллипса.
; где (x0; y0) – координаты центра эллипса.
3.
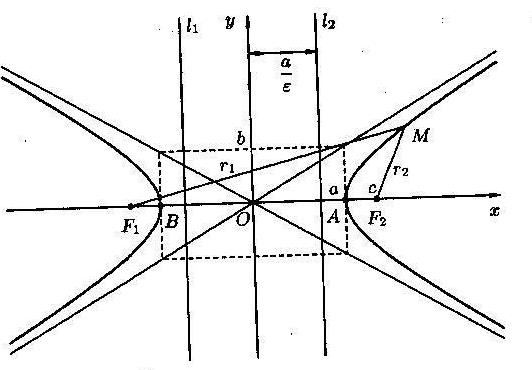 |
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы:
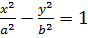 , где a – действительная, b – мнимая полуось гиперболы.
, где a – действительная, b – мнимая полуось гиперболы.
Координаты фокусов: F1(̶ c;0), F2(c;0), c – половина расстояния между фокусами. Числа a, b и c связаны соотношением 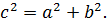 Точки A и B называются вершинами гиперболы, точка О – центром гиперболы, расстояния r1 и r2 от произвольной точки М гиперболы до её фокусов называются фокальными радиусами этой точки.
Точки A и B называются вершинами гиперболы, точка О – центром гиперболы, расстояния r1 и r2 от произвольной точки М гиперболы до её фокусов называются фокальными радиусами этой точки.
Число 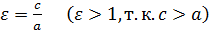 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
Фокальные радиусы определяются формулами: для точек правой ветви гиперболы: 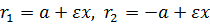 ;
;
для точек левой ветви: 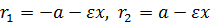 .
.
Прямоугольник, центр которого совпадает с точкой О, а стороны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы; они определяются уравнениями: 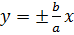 .
.
Две прямые l1 и l2, параллельные мнимой оси гиперболы и отстоящие от неё на расстоянии, равном  , называются директрисами гиперболы. Их уравнения
, называются директрисами гиперболы. Их уравнения 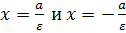 .
.
Замечания.
1) Если а=b, то гипербола называется равносторонней (равнобочной). Её уравнение имеет вид
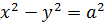 .
.
2)
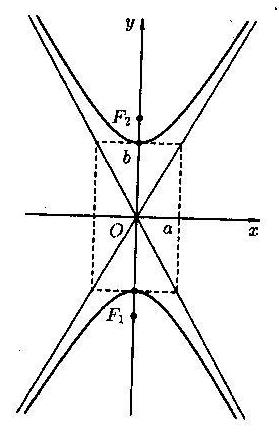 |
Если фокусы гиперболы лежат на оси Oy, то уравнение гиперболы имеет вид
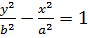 . Эксцентриситет этой гиперболы равен
. Эксцентриситет этой гиперболы равен 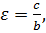 асимптоты определяются уравнениями
асимптоты определяются уравнениями 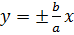 , а уравнения директрис
, а уравнения директрис 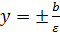 .
.
3)
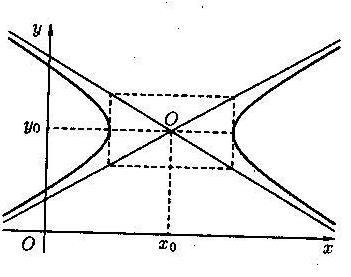 |
Уравнение гиперболы с осями, параллельными координатным, имеет вид
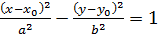 , где (x0;y0) – координаты центра гиперболы.
, где (x0;y0) – координаты центра гиперболы.
4. Параболой называется множество всех точек плоскости, каждая из которых равноудалена от заданной точки. Называемой фокусом, и заданной прямой, называемой директрисой.
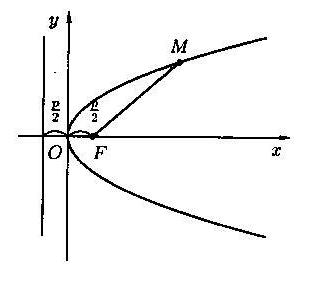 |
Каноническое уравнение параболы имеет вид
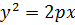 , где число p˃0, равное расстоянию от фокуса F до директрисы l, называется параметром параболы. Координаты фокуса F
, где число p˃0, равное расстоянию от фокуса F до директрисы l, называется параметром параболы. Координаты фокуса F 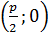 . Точка О(0; 0) называется вершиной параболы, длина r отрезка FM – фокальный радиус точки М, ось OX – ось симметрии параболы.
. Точка О(0; 0) называется вершиной параболы, длина r отрезка FM – фокальный радиус точки М, ось OX – ось симметрии параболы.
Уравнение директрисы параболы имеет вид: 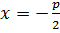 ;
;
Фокальный радиус вычисляется по формуле: 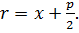
Замечания.
1) Парабола, симметричная относительно оси OY и проходящая через начало координат, имеет уравнение: 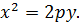
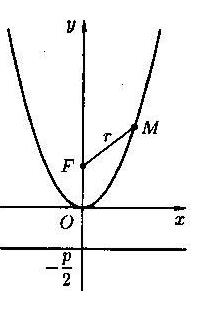 |
Фокусом параболы является точка F 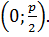
Уравнение директрисы этой параболы 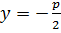 .
.
Фокальный радиус точки М параболы 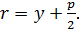
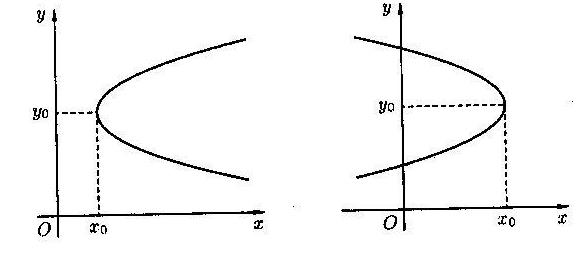
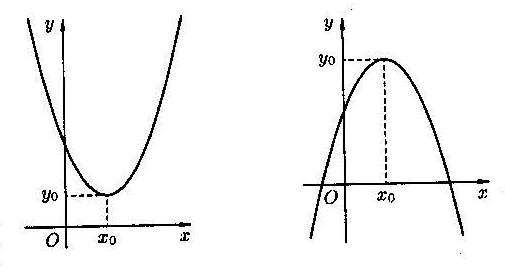
2) Различные параболы и их уравнения.
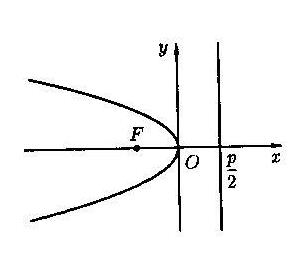 | 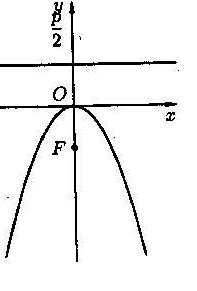 | ||
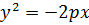
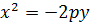
 |
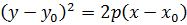
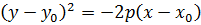
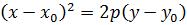
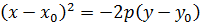
Задание № 6 (пример) Дано уравнение эллипса 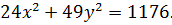 Найти:
Найти:
1) длины его полуосей;
2) координаты фокусов;
3) эксцентриситет эллипса;
4) уравнения директрис и расстояния между ними;
5) точки эллипса, расстояния от которых до левого фокуса F1 равно 12.
Решение. Запишем уравнение эллипса в виде канонического уравнения, разделив его обе части на 1176. Получим: 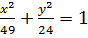 . Сравнивая с общим видом уравнения эллипса(
. Сравнивая с общим видом уравнения эллипса(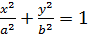 ), видно, что a2 =49, b2= 24, т. е. a =7, b =
), видно, что a2 =49, b2= 24, т. е. a =7, b = 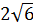 . Используя соотношение
. Используя соотношение 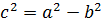 , находим c2 =49 ̶ 24=25, c =5. Следовательно, F1(̶ 5;0) и F2(5;0).
, находим c2 =49 ̶ 24=25, c =5. Следовательно, F1(̶ 5;0) и F2(5;0).
По формуле 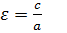 находим
находим 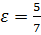 .
.
Уравнения директрис имеют вид 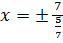 , т. е.
, т. е. 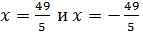 ; расстояния между ними
; расстояния между ними 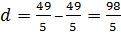 =19,6.
=19,6.
По формуле 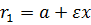 находим абсциссу точек, расстояния от которых до точки F1 равно 12: 12=7+
находим абсциссу точек, расстояния от которых до точки F1 равно 12: 12=7+ 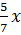 , т. е. x =7.
, т. е. x =7.
Подставляя значение x в уравнение эллипса. Найдём ординаты этих точек: 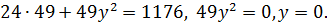 Условию задачи удовлетворяет точка А(7;0).
Условию задачи удовлетворяет точка А(7;0).