Практикой выработаны следующие правила округления результатов и погрешностей измерений.
1. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности.
Пример 4.
Х=2,0700, Δ=0,001 => Х≈2,070.
2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют.
Пример 5.
Число 253435 округляют до четырех значащих цифр. Получают 253400.
Число 235,435 ≈ 235,4
3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.
Пример 6.
18598 ≈ 18600 (до трех значащих цифр),
152,56 ≈ 153 (до трех значащих цифр).
4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или равны нулю, то последнюю сохраняемую цифру не изменяют если она четная, и увеличивают, если она нечетная.
Пример 7.
При сохранении двух значащих цифр
22,5 округляют до 22,
23,5 округляют до 24.
10.2. Систематические погрешности. Обнаружение и исключение.
В настоящее время, особенно после введения одного из основополагающих метрологических стандартов ГОСТ 8.009-84 “ГСИ. Основные метрологические характеристики средств измерений”, понятие “систематическая погрешность” несколько изменилось по
отношению к определению, данному ГОСТ 16263-70 “ГСИ. Метрология Термины и определения”. Систематическая погрешность считается специфической, “вырожденной” случайной величиной, обладающей некоторыми, но не всеми свойствами случайной величины, изучаемой в теории вероятностей и математической статистике. Свойства систематической погрешности. которые необходимо учитывать объединении составляющих погрешности, отражаются такими характеристиками, что и свойства “настоящих” случайных величин - дисперсией (СКО) и коэффициентом взаимной корреляции.
Систематическая погрешность представляет собой определенную функцию влияющих факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, условий их применения, а также индивидуальных качеств наблюдателя. В метрологической практике при оценке систематических погрешностей должно учитываться влияние следующих основных факторов:
1. Объект измерения. Перед измерением он должен быть достаточно хорошо изучен с целью корректного выбора его модели. Чем полнее модель соответствует исследуемому объекту, тем точнее могут быть получены результаты измерения. Например, кривизна земной поверхности может не учитываться при измерении площади сельскохозяйственных угодий, так как она не вносит ощутимой погрешности, однако при измерении площади океанов ею пренебрегать уже нельзя.
2. Субъект измерения. Его вклад в погрешность измерения необходимо уменьшать путем подбора операторов высокой квалификации и соблюдения требований эргономики при разработке СИ.
З. Метод и средство измерений. Чрезвычайно важен их правильный выбор, который производится на основе априорной информации об объекте измерения. Чем больше априорной информации, тем точнее может быть проведено измерение. Основной вклад в систематическую погрешность вносит, как правило, методическая погрешность.
4. Условия измерения. Обеспечение и стабилизация нормальных условий являются необходимыми требованиями для минимизации дополнительной погрешности, которая по своей природе, как правило, является систематической.
Систематические погрешности принято классифицировать до двум признакам.
По характеру изменения во времени они делятся на постоянные и переменные. Постоянными называются такие по грешности измерения, которые остаются неизменными в течение всей серии измерений. Например, погрешность от того, что неправильно установлен ноль стрелочного электроизмерительного прибора, погрешность от постоянного дополнительного веса на чашке весов и т.д. Переменными называются погрешности, изменяющиеся в процессе измерения. Они делятся на монотонно изменяющиеся, периодические и изменяющиеся по сложному закону. Если в процессе измерения систематическая погрешность монотонно возрастает или убывает, ее называют монотонно изменяющейся. Например, она имеет место при постепенном разряде батареи, питающей средство измерений. Периодической называется погрешность, значение которой является периодической функцией времени. Примером может служить погрешность, обусловленная суточными колебаниями напряжения силовой питающей сети, температуры окружающей среды и др. Систематические погрешности могут изменяться и по более сложному закону, обусловленному какими-либо внешними причинами.
По причинам возникновения погрешности делятся на методические, инструментальные и личные (субъективные). Эти погрешности подробно рассмотрены выше.
Результаты наблюдений, полученные при наличии систематической погрешности, называются неислравленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. Это может быть достигнуто следующими путями:
· устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;
· определением поправок и внесением их в результат измерения;
· оценкой границ неисключенных систематических погрешностей.
Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения
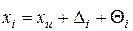 ,
,
где хи - истинное значение измеряемой величины;
Δ - i-я случайная погрешность;
Θ - i-я систематическая погрешность.
После усреднения результатов многократных измерений получаем среднее арифметическое значение измеряемой величины
 .
.
Если систематическая погрешность постоянна во всех измерениях, т.е. Θi=Θ, то
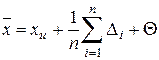 .
.
Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.
Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Постоянные инструментальные систематические погрешности обычно выявляют посредством поверки средства измерений.
Поверкой называют определение метрологическим органом погрешностей средства измерений и установление пригодности средства измерений к применению. Обнаруженные путем поверки систематические погрешности исключаются из результата измерения путем введения поправки.
Пример.
При измерении напряжения в сети показания вольтметра 225 В. В свидетельстве о поверке указано, что на этой отметке шкалы систематическая погрешность вольтметра равна +3 В. С учетом поправки напряжение в сети равно 225-3=222 В.
Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже. Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.
Для устранения постоянных систематических погрешностей применяют следующие методы.
Графический метод. Для обнаружения изменяющейся систематической погрешности рекомендуется построить график, на котором нанесены результаты наблюдений в той последовательности, в какой они были получены. Простейшим случаем является погрешность, прогрессирующая по линейному закону, например, пропорционально времени.

 х
х
 х2
х2
 х1
х1
х0
 t1 t2 t
t1 t2 t
Рис 10.2. Линейное изменение систематической погрешности.
Такие погрешности могут быть оценены и исключены следующим образом. Если известно, что при измерении постоянной величины х0 систематическая погрешность изменяется линейно во времени, т.е.
х=х0 +Сt (где С=const),
То для ее исключения достаточно сделать 2 наблюдения х1 и х2 с фиксацией времени t1 и t2, тогда искомое значение величины будет
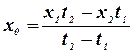 . (10.1.)
. (10.1.)
Однако, далеко не всегда систематическая погрешность изменяется по линейному закону. В этом случае для контроля систематической погрешности применяется метод симметричных наблюдений.
Выполняют несколько наблюдений через равные промежутки времени. Вычисляют средние арифметические симметрично расположенных отсчетов
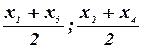 .
.
Теоретически, при линейной зависимости погрешности от времени, эти средние арифметические должны быть равны. Убедившись, что погрешность изменяется по линейному закону, находят результат по вышеприведенной формуле.
 х
х


 х5
х5

 х4
х4

 х3
х3
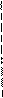
 х2
х2

 х1
х1
х0 
t1 t2 t3 t4 t5 t
Рис.10.3. Иллюстрация метода симметричных наблюдений
Систематические составляющие, обусловленные несовершенством методов измерения, ограниченной точностью расчетных формул, положенных в основу измерений, влиянием средств измерений на объект, свойства которого измеряются, относятся к методическим погрешностям. Единых рекомендаций по обнаружению и оцениванию методических составляющих систематической погрешности нет. Задача решается в каждом конкретном случае индивидуально, на основе анализа примененного метода измерений, результаты которого часто зависят от квалификации и опыта экспериментатора.
Личные систематические погрешности связаны с индивидуальными особенностями наблюдателя. Для уменьшения этого вида погрешностей надо точно соблюдать правила эксплуатации средств измерений и иметь навыки работы с измерительной техникой.
В практике измерений применяются несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку.
Метод замещения. Этот метод дает наиболее полное решение задачи компенсации постоянной систематической погрешности и представляет собой разновидность метода сравнения. Сравнение производится путем замены измеряемой величины известной величиной таким образом, чтобы воздействием известной величины привести средство измерения в то состояние, которое оно имело при воздействии измеряемой величины.
Пример. Взвешивание на пружинных весах, у которых имеется постоянная систематическая погрешность (например, из-за смещения шкалы).
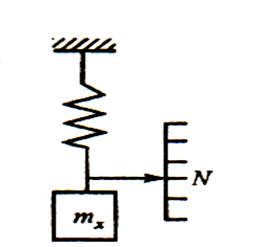
Рис.10.4. Измерение массы тела методом замещения
Взвешивание производится в два приема. Вначале на чашу весов помещают взвешиваемое тело массой mх и отмечают положение указателя (на отметке N). Затем взвешиваемое тело замещают гирями такой массы m0, чтобы вновь добиться прежнего отклонения указателя N. Очевидно, что при одинаковости отклонений указателя mх = m0 систематическая погрешность весов не скажется на результате измерений.
Метод противопоставления. Рассмотрим данный метод на следующем примере.
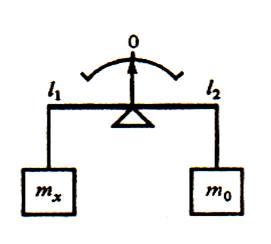
Рис.10.5. Измерение массы тела методом противопоставления
Пример. Взвешивание на рычажных равноплечих весах. Условие равновесия весов mхl1= m0l2, отсюда mх = m0 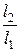 . Если длины плеч одинаковы l1= l2, то mх = m0. Если же l1≠ l2 (из-за технологического разброса длин плеч при их изготовлении), то при взвешивании каждый раз возникает систематическая погрешность
. Если длины плеч одинаковы l1= l2, то mх = m0. Если же l1≠ l2 (из-за технологического разброса длин плеч при их изготовлении), то при взвешивании каждый раз возникает систематическая погрешность 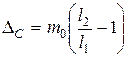 . Для исключения этой погрешности взвешивание производится в два этапа.
. Для исключения этой погрешности взвешивание производится в два этапа.
Сначала взвешивают груз mх, уравновешивая весы гирями массой m01. При этом mхl1= m01l2. Затем взвешиваемый груз перемещают на ту чашу весов, где прежде были гири и вновь уравновешивают весы массой гирь m02. Теперь получим mх=m02. Исключив из равенств отношение l2/l1 найдем 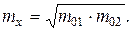
Как видно из формулы, длины плеч не входят в окончательный результат взвешивания.
Специальные статистические методы.
К ним относятся способ последовательных разностей, дисперсионный анализ и др. Рассмотрим более подробно первый из них.
Способ последовательных разностей (критерий Аббе) применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результата измерений можно оценить двумя способами: обычным
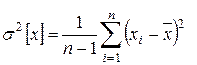
и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей (xi+1-xi)2
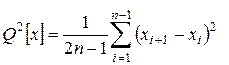 .
.
Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то σ2[х] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на σ2[х] влияют вариации  . В то же время изменения центра группирования
. В то же время изменения центра группирования  весьма мало сказываются на значениях последовательных разностей
весьма мало сказываются на значениях последовательных разностей 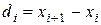 поэтому смещения
поэтому смещения  почти не отражается на значении Q2[х].
почти не отражается на значении Q2[х].
Отношение 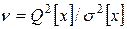 является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как Р(ν<νq)=q, где q=1-P – уровень значимости, Р - доверительная вероятность. Значения νq для разных уровней значимости q и числа наблюдений n приведены в таблице 1.
является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как Р(ν<νq)=q, где q=1-P – уровень значимости, Р - доверительная вероятность. Значения νq для разных уровней значимости q и числа наблюдений n приведены в таблице 1.
Значения критерия Аббе
| n | νq при q, равном | n | νq при q, равном | ||||
| 0,001 | 0,01 | 0,05 | 0,001 | 0,01 | 0,05 | ||
| 0,295 0,208 0,182 0,185 0,202 0,221 0,241 0,260 0,278 | 0,313 0,269 0,281 0,307 0,331 0,354 0,376 0,396 0,414 | 0,390 0,410 0,445 0,468 0,491 0,512 0,531 0,548 0,564 | 0,295 0,311 0,327 0,341 0,355 0,368 0,381 0,393 | 0,431 0,447 0,461 0,474 0,487 0,499 0,510 0,520 | 0,578 0,591 0,603 0,614 0,624 0,633 0,642 0,650 |
Если полученное значение критерия Аббе меньше νq ‚ при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.
Пример.
Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных во втором столбце табл..2
Результаты наблюдений
| n | xi | 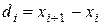
| 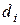
| 
| 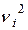
|
| 13,4 | - | - | -0,6 | ||
| 13,3 | -0,1 | 0,01 | -0,7 | 0,49 | |
| 14,5 | +1,2 | 1,44 | +0,5 | 0,25 | |
| 13,8 | -0,7 | 0,49 | -0,2 | 0,04 | |
| 14,5 | +0,7 | 0,49 | +0,5 | 0,25 | |
| 14,6 | +0,1 | 0,01 | +0,6 | 0,86 | |
| 14,1 | -0,5 | 0,26 | +0,1 | 0,01 | |
| 14,3 | +0,2 | 0,04 | +0,3 | 0,09 | |
| 14,0 | +0,3 | 0,09 | 0,0 | 0,0 | |
| 14,3 | +0,3 | 0,09 | +0,3 | 0,09 | |
| 13,2 | -1,1 | 1,21 | -0,8 | 0,64 | |
| Σ 154,0 | -0,2 | 4,12 | 0,0 | 2,58 |
Для приведенного ряда результатов вычисляем: среднее арифметическое  =154,0/11=14; оценку дисперсии σ2[х]=2,58/10=0,258; значение Q2[х]=4,12/(2 10)=0,206; критерий Аббе ν=0,206/0,258=0,8. Как видно из табл.1, для всех уровней значимости (q=0,001; 0,01 и 0,05) при n=11 имеем ν<νq, т.е. подтверждается нулевая гипотеза о постоянстве центра группирования. Следовательно, условия измерений для приведенного ряда оставались неизменными и систематических расхождений между результатами наблюдений нет.
=154,0/11=14; оценку дисперсии σ2[х]=2,58/10=0,258; значение Q2[х]=4,12/(2 10)=0,206; критерий Аббе ν=0,206/0,258=0,8. Как видно из табл.1, для всех уровней значимости (q=0,001; 0,01 и 0,05) при n=11 имеем ν<νq, т.е. подтверждается нулевая гипотеза о постоянстве центра группирования. Следовательно, условия измерений для приведенного ряда оставались неизменными и систематических расхождений между результатами наблюдений нет.
Суммирование систематических погрешностей.
Независимо от того, к какому виду относится измерение, является ли оно прямым, косвенным, совместным или совокупным, систематическая погрешность результата измерения оценивается, как правило, по ее известным составляющим. Поскольку в каждом конкретном случае каждая систематическая составляющая является либо постоянной, либо известен закон ее изменения, то суммарная (результирующая) погрешность представляет собой алгебраическую сумму составляющих:
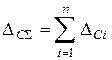
10.3. Случайные погрешности. Вероятностное описание результатов и погрешностей
Когда при проведении в одинаковых условиях повторных измерений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Эта погрешность возникает вследствие одновременного воздействия на результат многих случайных возмущений и сама является случайной величиной. В этом случае предсказать результат отдельного измерения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от хmin до хmax, где хmin и хmax – соответственно нижняя и верхняя граница разброса.
Для установления вероятностных (статистических) закономерностей появления случайных погрешностей и количественной оценки результата измерений и его случайной погрешности используются методы теории вероятностей и математической статистики.
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.
Рассмотрим формирование дифференциального закона.
1. Проведем n измерений одной величины Х.
2. Получим группу наблюдений х1; х2,…,хn.
3. Расположим результаты в порядке возрастания от хmin до хmax.
4. Найдем размах ряда L=хmax - хmin.
5. Разделим размах ряда на k равных интервалов ∆l=L/k.
6. Подсчитаем количество наблюдений nk, попадающих в каждый интервал.
7. Изобразим полученные результаты графически (по оси абсцисс – значения физической величины с границами интервалов; по оси ординат – относительная частота попаданий nk/n.
8. Достроив по полученным точкам соответствующие прямоугольники получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.
Пример. N=50 измерений.
| N интервала | |||||
| nk | |||||
| nk/n | 0,1 | 0,2 | 0,36 | 0,22 | 0,12 |
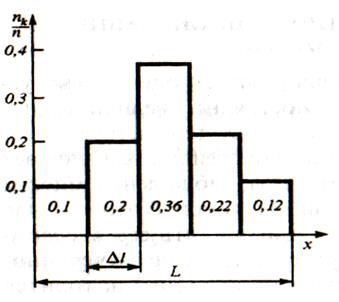
Рис.10.6. Гистограмма
Если распределение случайной величины статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Следовательно, по гистограмме можно предсказывать распределение результатов измерений по интервалам.
При бесконечном увеличении числа наблюдений n→∞ и бесконечном уменьшении ширины интервалов Δl→0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), которая называется кривой плотности распределения вероятностей случайной величины, а уравнение ее описывающие дифференциальным законом распределения.
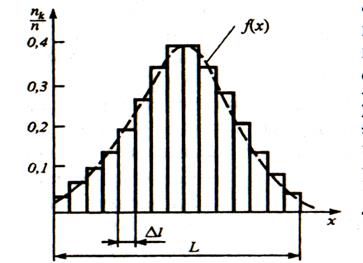
Рис.10.7. Кривая плотности распределения вероятностей
Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:
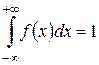
Если известен закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х1 до х2
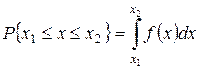 .
.
Кроме непрерывных случайных величин в метрологической практике встречаются и дискретные случайные величины. Пример распределения дискретной случайной величины приведен на рис.10.8.
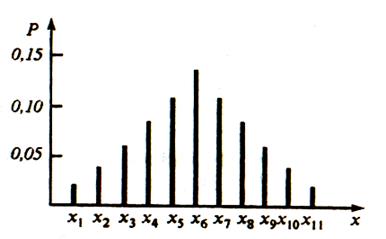
Рис.10.8. Распределение дискретной случайной величины
Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения. Причем, если усредняются величины, отсчитываемые от начала координат, моменты называют начальными, а если от центра закона распределения, то центральными.
Начальный момент k-го порядка определяется формулой
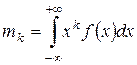 ;
;
 ,
,
где рi – вероятность появления дискретной величины.
Здесь и ниже первая формула относится к непрерывным, а вторая к дискретным случайным величинам.
Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины (k=1),
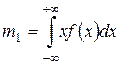 ;
;
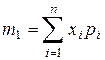 .
.
Центральные моменты k-го порядка рассчитываются по формулам:
 ;
;
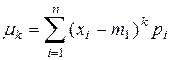 .
.
Из центральных моментов особенно важную роль играет второй момент (k=2), дисперсия случайной величины D
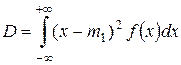 ;
;
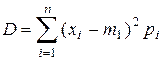 .
.
Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии – средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.