Нетрудно видеть, что процедура построения механического аналога, моделирующего продольную динамику стержня, легко обобщается на случай любой осесимметричной конструкции (оболочки, осесимметричного упругого тела), возбуждаемой вдоль оси симметрии.
Очевидно, что уравнения колебаний осесимметричной системы можно записать в векторно-матричном виде, по структуре аналогичном (9.1).

| (9.22) |
Здесь  – матрица масс,
– матрица масс,  – вектор кинематических параметров,
– вектор кинематических параметров,  ‑ матричный дифференциальный оператор либо матрица жесткости при конечноэлементной постановке задачи,
‑ матричный дифференциальный оператор либо матрица жесткости при конечноэлементной постановке задачи,  – вектор внешних сил.
– вектор внешних сил.
В осесимметричном случае удобно пользоваться цилиндрической системой координат x, r,q (x – вдоль оси, r – по радиусу, q – по кольцу).
В осесимметричном случае нагружения перемещения зависят только от x, r и времени 
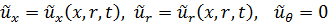 . .
| (9.23) |
В этом случае в уравнении (9.22) под  подразумевается вектор
подразумевается вектор
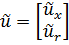 . .
|
При кинематическом возбуждении, например, осесимметричной оболочки вдоль оси симметрии граничное условие в сечении x= 0 по контуру  запишется так
запишется так

| (9.24) |
Дополнительно на контур оболочки r=R при x= 0 могут накладываться следующие граничные условия:
| неподвижный контур в радиальном направлении | 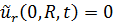 момент отсутствует
момент отсутствует
| (9.25) |
| закрепление контура по радиальному перемещению и углу поворота | 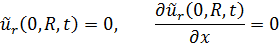
| |
| подвижный в радиальном направлении контур | (моменты и перерезывающие силы отсутствуют) |
При этом верхний торец рассматриваемой осесимметричной системы считается свободным. Решение уравнения (9.22) отыскивается в виде
 , здесь , здесь 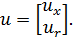
| (9.26) |
При этом осевая компонента  вновь введённой функции
вновь введённой функции  с учётом (9.24) и (9.26) будет удовлетворять условию
с учётом (9.24) и (9.26) будет удовлетворять условию

| (9.27) |
Подставляя соотношение (9.26) в (9.22) приходим к уравнению, аналогичному по структуре (9.4),

| (9.28) |
Здесь под  подразумеваются некоторые распределенные по оболочке осесимметричные силы.
подразумеваются некоторые распределенные по оболочке осесимметричные силы.
Для построения механического аналога, моделирующего продольные колебания осесимметричной конструкции, необходимо предварительно решить соответствующую уравнению (9.28) задачу о собственных колебаниях с граничными условиями (9.27) и любым из вариантов (9.25) (консольно закрепленной вдоль оси х оболочки)
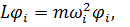 где где  . .
| (9.29) |
Вся дальнейшая процедура построения механического аналога в виде кинематически возбуждаемого осциллятора аналогична (9.6)-(9.19) с той лишь разницей, что в формулах (9.6)-(9.19) обобщённые скалярные операции проводятся с одномерными векторами, а в случае возбуждения осесимметричного тела вдоль оси симметрии в этих формулах под  и
и  подразумеваются двумерные вектора
подразумеваются двумерные вектора
  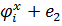  . .
| (9.30) |
Структура формул для эквивалентных масс, жесткостей и обобщённых сил (9.14), (9.15) для осесимметричных тел полностью сохраняется.
Напомним, что с учетом (9.30) для нормированных по единичной массе форм колебаний параметры имеют вид
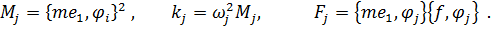
| (9.31) |
При этом только следует иметь в виду, что обобщённое скалярное произведение, например, для осесимметричного упругого тела, будет иметь вид
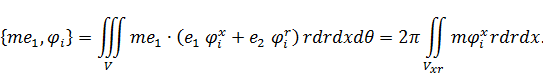
| (9.32) |


| (9.33) |
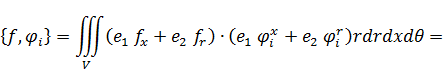

| (9.34) |
Важную роль в построении расчётных моделей для расчёта нагрузок играют аналоги, моделирующие гидроупругие колебания баков с топливом, так как они существенно влияют на продольные нагрузки РН.
Динамическое воздействие жидкости на конструкцию при осесимметричных колебаниях топливных баков может определяться вариационным методом [4], включая метод конечных элементов [5], и учитываться набором осцилляторов продольных колебаний [1, 3, 6]. Одним из распространенных методов определения параметров продольных осцилляторов, учитывающих гидроупругие колебания топливных баков, является метод "виртуальных масс" (жидкость в нем моделируется потенциалом простого слоя см. […]).