Приложения
Приложение 1. Варианты индивидуальных заданий
Задания 1 - 5 решить с использованием необходимых и достаточных условий
Задание №1
Дана функция y=f(x) (таблица). Найти:
а) Безусловные экстремумы функции y=f(x).
б) Условные экстремумы функции y = f (x) на отрезке [ a, b ]:
| Вар-т | Функция | [ a, b ] | Вариант | Функция | [ a, b ] | |
| y =ln(x 2-2 x +2) | [0; 3] | y = 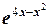
| [1; 3] | |||
| y =3 x /(x 2+1) | [0; 5] | y =(x 5-8)/ x 4 | [-3; -1] | |||
| y =(2 x -1)/(x -1)2 | [-1/2; 0] | y =(e 2 x +1) e - x | [-1; 2] | |||
| y =(x +2) e 1- x | [-2; 2] | y = x ln x | [1/ e 2; 1] | |||
| y =ln(x 2-2 x +4) | [-1; 3/2] | y = x 3 ex +1 | [-4; 0] | |||
| y = x 3/(x 2- x +1) | [-1; 1] | y = x 2-2 x +2/(x -1) | [-1; 3] | |||
| y =((x +1)/ x)3 | [1; 2] | y =(x +1) 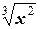
| [-4/5; 3] | |||
y = 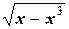
| [-2; 2] | y = 
| [-3; 3] | |||
y =4- 
| [0; 1] | y =(ln x)/ x | [1; 4] | |||
| y =(x 3+4)/ x 2 | [1; 2] | y =3 x 4-16 x 3+2 | [-3; 1] | |||
| y = xex | [-2; 0] | y = x 5-5 x 4+5 x 3+1 | [-1; 2] | |||
| y =(x -2) ex | [-2; 1] | y =(3- x) e - x | [0; 5] | |||
| y =(x -1) e - x | [0; 3] | y =  +cos x +cos x
| [0; p/2] | |||
| y = x /(9- x 2) | [-2; 2] | y =108 x - x 4 | [-1; 4] | |||
| y =(1+ln x)/ x | [1/ e; e ] | y = x 4/4-6 x 3 | [14; 20] |
Задание №2
Исследовать на безусловный экстремум функцию:
а) f (x, y)= ax 2+2 xy + by 2-2 x -3 y:
| № в-та | a | b | № в-та | a | b | № в-та | a | b | № в-та | a | b |
б) f (x, y)= ax 3+ ax 2 y + bx +  y 3+ cy:
y 3+ cy:
| № в-та | a | b | c | № в-та | a | b | c |
в) f (X)= a  + b
+ b 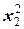 + c
+ c  -2 x 1 x 2- x 1+3 x 2:
-2 x 1 x 2- x 1+3 x 2:
| № в-та | a | b | c | № в-та | a | b | c |
г) f (X)= a  + b
+ b 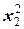 + c
+ c  +3 x 1 x 3-4 x 1+2 x 3:
+3 x 1 x 3-4 x 1+2 x 3:
| № в-та | a | b | c | № в-та | a | b | c |
| -2 | -4 | ||||||
| -9 | -2 | ||||||
| -3 | -2 | ||||||
| -3 | -4 | ||||||
| -2 | -2 | ||||||
| -2 | -2 | ||||||
| -2 | -4 | ||||||
| -6 | -2 | ||||||
| -2 | -2 | ||||||
| -2 | -4 |
д) f (X)= a  + b
+ b 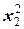 + c
+ c  - x 2 x 3+2 x 2-3 x 3:
- x 2 x 3+2 x 2-3 x 3:
| № в-та | a | b | c | № в-та | a | b | c |
| -3 | -2 | -3 | -5 | -2 | -1 | ||
| -2 | -4 | -6 | -4 | -1 | -4 | ||
| -3 | -6 | -8 | -5 | -2 | -1 | ||
| -4 | -8 | -2 | -2 | -3 | -2 | ||
| -5 | -2 | -4 | -3 | -4 | -3 | ||
| -2 | -6 | -9 | -4 | -3 | -4 | ||
| -3 | -9 | -2 | -5 | -2 | -3 | ||
| -4 | -2 | -3 | -2 | -4 | -2 | ||
| -5 | -3 | -4 | -3 | -4 | -1 | ||
| -2 | -8 | -2 | -4 | -5 | -2 |
е) f (x 1, x 2, x 3)= a  + b
+ b 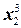 + c
+ c  +4 x 1 x 3-3 x 3+6:
+4 x 1 x 3-3 x 3+6:
| № в-та | a | b | c | № в-та | a | b | c |
Задание №3
Исследовать на условный экстремум функцию:
а) f (x 1, x 2)= ax 1+ bx 2+ c при условии 4  + c
+ c 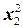 =9:
=9:
| № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c |
б) f (x 1, x 2)= a  +2 x 1 x 2+ b
+2 x 1 x 2+ b 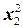 при условии 4
при условии 4  + c
+ c 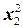 =9:
=9:
| № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c |
| -2 | 64/19 | 16/13 | |||||||||||||
| 16/5 | 16/9 | 18/13 | 16/9 | ||||||||||||
| 50/33 | 18/25 | 18/13 | |||||||||||||
| 162/25 | 98/61 | 50/43 | |||||||||||||
| 9/2 | 18/19 |
Задание №4
Исследовать на условный экстремум функцию:
а) f (x 1, x 2)= a  + b
+ b 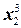 при условии
при условии  +
+ 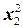 £ c:
£ c:
| № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c |
б) f (x 1, x 2)=(x 1- a 1)2+(x 2- a 2)2при условиях 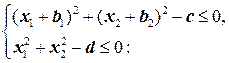
| № в-та | a 1 | a 2 | b 1 | b 2 | c | d | № в-та | a 1 | a 2 | b 1 | b 2 | c | d |
в) f (x 1, x 2)=(x 1- a 1)2+(x 2- a 2)2при условиях 
| № в-та | a 1 | a 2 | b 1 | b 2 | d | № в-та | a 1 | a 2 | b 1 | b 2 | d |
Задание №5
Исследовать на условный экстремум функцию
f (x 1, x 2)=(x 1- a 1)2+(x 2- a 2)2при условиях 
| № в-та | a 1 | a 2 | b 1 | b 2 | c | d | № в-та | a 1 | a 2 | b 1 | b 2 | c | d |
Задание №6
Решить задачу f (x)= ax 2+ bx + c ® min методом:
а) равномерного поиска;
б) деления интервала пополам:
| № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c |
| -6 | -2 | -8 | -7 | ||||||||||||
| -3 | -2 | -6 | -7 | ||||||||||||
| -3 | -3 | -8 | -3 | ||||||||||||
| -3 | -4 | -8 | -5 | ||||||||||||
| -4 | -6 | -3 | -2 |
Задание №7
Найти локальный минимум функции Задания №2 методом:
а) методом градиентного спуска с постоянным шагом;
б) методом Ньютона.
Задание №8
Решить задачу условной оптимизации с целевой функцией из Задания 3 б) при условии ax 1+ bx 2+ c =0:
а) методом последовательной безусловной оптимизации;
б) методом проекции градиента:
| № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c | № в-та | a | b | c |
| -6 | -3 | -8 | -6 | ||||||||||||
| -7 | -2 | -6 | -7 | ||||||||||||
| -3 | -4 | -8 | -4 | ||||||||||||
| -9 | -4 | -2 | -5 | ||||||||||||
| -4 | -6 | -3 | -3 |
Приложение 2. Образец решения индивидуального задания
Задание 1. Дана функция y=4x3+9x2+6x-1. Найти:
а) Безусловные экстремумы функции.
б) Условные экстремумы функции на отрезке [-2, 3].
Решение. а) Способ 1 (с применением первого достаточного условия). Для того, чтобы исследовать функцию одной переменной на безусловный экстремум (то есть найти для функции точки экстремумов, определить их характер и вычислить значения функции в этих точках) с применением первого достаточного условия, достаточно:
1. Найти у функции производную.
2. Решив уравнение y ¢=0, найти стационарные точки функции.
3. Решив неравенство y ¢>0 (y ¢<0), определить, меняет ли знак производная в стационарных точках.
4. По характеру перемены знака производной определить, какие из стационарных точек являются точками максимума, какие - точками минимума, какие - ни теми, ни другими.
5. Вычислить значения экстремумов функции (то есть вычислить значения функции в точках экстремума).
Итак:
1. Найдём у функции производную: y ¢=12 x 2+18 x +6.
2. Решая уравнение y ¢=0, найдём стационарные точки функции:
y ¢=0 Û 12 x 2+18 x +6=0 Û 2 x 2+3 x +1=0, D =32-4×2×1=1, x 1, 2=  =
= 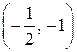 ,
,
то есть x 1=  , x 2=-1 - стационарные точки функции.
, x 2=-1 - стационарные точки функции.
3. Решая неравенство y ¢>0, определяем, меняет ли знак производная в стационарных точках (используя метод интервалов):
y ¢>0 Û 2 x 2+3 x +1=0 Û 2(x +  )(x +1)>0 Û x Î(-
)(x +1)>0 Û x Î(- 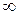 ; -1)È(
; -1)È(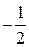 ; +
; + 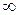 ).
).
В частности, это означает, что y ¢<0 Û x Î(-1;  ), то есть y ¢ меняет знак на противоположный в обеих стационарных точках.
), то есть y ¢ меняет знак на противоположный в обеих стационарных точках.
4. В точке x 1=  y ¢ меняет знак с «-» на «+». Поэтому эта точка - точка минимума. В точке x 2=-1 y ¢ меняет знак с «+» на «-». Поэтому эта точка - точка максимума.
y ¢ меняет знак с «-» на «+». Поэтому эта точка - точка минимума. В точке x 2=-1 y ¢ меняет знак с «+» на «-». Поэтому эта точка - точка максимума.
5. Вычисляем значения экстремумов функции в точках экстремума:
f min(x)= f  =4
=4  +9
+9 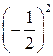 +6
+6  -1=
-1=  ,
,
f max(x)= f (-1)=4(-1)3+9(-1)2+6(-1)-1=-2.
Способ 2 (с применением второго достаточного условия). Для того, чтобы исследовать функцию на безусловный экстремум с применением второго достаточного условия, достаточно:
1. Найти у функции производную.
2. Решив уравнение y ¢=0, найти стационарные точки функции.
3. Найти у функции производную второго порядка.
4. Определить, какие из стационарных точек являются точками максимума, какие - точками минимума, какие - ни теми, ни другими. Для этого вычисляем значение второй производной в стационарных точках.
5. Вычислить значения экстремумов функции.
Итак:
1. y ¢=12 x 2+18 x +6.
2. y ¢=0 Û x 1=  и x 2=-1.
и x 2=-1.
3. Найдём у функции производную второго порядка: y ¢¢ =24 x +18.
4. Подставляя в y ¢¢ стационарные точки. Определяем, какие из них являются точками максимума, какие - точками минимума: y ¢¢ (-1)=24(-1)+18=-6<0. Поэтому x =-1 - точка максимума.
Далее, y ¢¢  =24
=24  +18=6>0. Поэтому x =
+18=6>0. Поэтому x =  - точка минимума.
- точка минимума.
5. f max(x)= f (-1)=-2, f min(x)= f  =
=  .
.
б) Для того, чтобы исследовать функцию y = f (x) одной переменной на условный экстремум на отрезке [ a, b ], достаточно:
1. Найти производную функции y.
2. Решив уравнение y ¢=0, найти стационарные точки функции.
3. Вычислить значения функции в стационарных точках и на концах отрезка [ a, b ].
4. Выделить из значений функции, вычисленных в пункте 3, наибольшее и наименьшее значения.
Итак,
1. Найдём у функции производную: y ¢=12 x 2+18 x +6.
2. Решая уравнение y ¢=0, найдём стационарные точки функции:
y ¢=0 Û x 1= 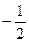 , x 2=-1 - стационарные точки функции
, x 2=-1 - стационарные точки функции
(подробности приведены при решение задания а))
3. Вычислим значения функции в стационарных точках и на концах отрезка [-2, 3]:
f (-1)=-2, f 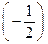 =
=  (подробности см. решение задания а)),
(подробности см. решение задания а)),
f (-2)=4(-2)3+9(-2)2+6(-2)-1=-3, f (3)=4×33+9×32+6×3-1=206.
4. Сравнивая полученные в предыдущем пункте значения функции, выделяем из них наибольшее и наименьшее значения: f наим(x)= f (-2)=-3, f наиб(x)= f (3)=206.
Ответ: а) x =-1 - точка локального максимума, f max(x)=-2,
x =  - точка локального минимума, f min(x)=
- точка локального минимума, f min(x)=  .
.
б) f наим(x)=-3 достигается в точке x =-2,
f наиб(x)=206 достигается в точке x =3.
Задание 2. Исследовать на безусловный экстремум функцию:
а) f (x, y)=2 x 2+3 xy +2 y 2+3 x -3 y +2;
б) f (x, y)=6 x 3+6 x 2 y -3 x + 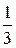 y 3-
y 3-  y;
y;
в) f (x 1, x 2, x 3)=-  -2
-2  -3
-3 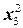 - x 1-2 x 2+ x 1 x 2;
- x 1-2 x 2+ x 1 x 2;
г) f (x 1, x 2, x 3)=2  +2
+2  +3
+3 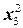 -2 x 1+3 x 2+2 x 1 x 3;
-2 x 1+3 x 2+2 x 1 x 3;
д) f (x 1, x 2, x 3)=  +2
+2  -
- 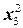 +4 x 1+ x 2-2 x 1 x 2;
+4 x 1+ x 2-2 x 1 x 2;
е) f (x 1, x 2, x 3)=2  +
+  +
+ 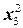 + x 1 x 3-12 x 2+5 x 3+6.
+ x 1 x 3-12 x 2+5 x 3+6.
Решение. а) Для того, чтобы исследовать функцию на безусловный экстремум (то есть для того, чтобы найти для функции точки экстремумов, определить их характер и вычислить значения функции в этих точках), достаточно:
1. Найти у функции частные производные первого порядка.
2. Решив систему
 =0, i =1, 2, …, n, (1)
=0, i =1, 2, …, n, (1)
найти стационарные точки функции.
3. Найти у функции частные производные второго порядка и составить матрицу Гессе
H (X) = 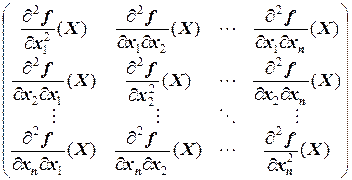 .
.
4. Определить, какие из стационарных точек являются точками максимума, какие - точками минимума, какие - ни тем, ни другим. Для этого используем информацию о знакоопределённости матрицы Гессе в стационарных точках.
5. Вычислить значения функции в точках экстремумов.
Итак, действуем по вышеуказанной схеме:
1. Найдём у функции частные производные первого порядка:  =4 x +3 y +3,
=4 x +3 y +3,  =3 x +6 y -3.
=3 x +6 y -3.
2. Решая систему (1), найдём стационарные точки функции:
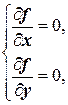 Û
Û  Û
Û 
Применив к последней системе, например, правило Крамера, получаем D=  =5, D x =
=5, D x = 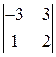 =-9, D y =
=-9, D y =  =7, (x, y)=
=7, (x, y)=  =
=  , то есть X 0=
, то есть X 0= 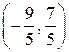 - стационарная точка.
- стационарная точка.
3. Найдём у функции частные производные второго порядка и составим матрицу Гессе H (X)= 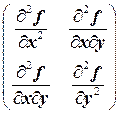 :
: 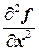 =4,
=4,  =
=  =3,
=3, 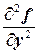 =6, H (X)=
=6, H (X)=  .
.
4. Так как D=  =15>0, то в точке X 0=
=15>0, то в точке X 0= 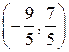 функция достигает своего экстремума. При этом
функция достигает своего экстремума. При этом 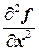 =4>0. Поэтому в точке X 0 функция достигает минимума.
=4>0. Поэтому в точке X 0 функция достигает минимума.
5. Вычисляем значение функции в точке минимума:
f min(x, y)= f 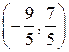 =2
=2  +3
+3  ×
×  +2×
+2×  +3
+3  -3×
-3× 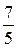 +2=
+2=  .
.
б) Действуем по вышеописанной схеме:
1. Найдём у функции частные производные первого порядка:  =18
=18 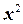 +12 xy -3,
+12 xy -3,  =6 x 2+ y 2-
=6 x 2+ y 2-  .
.
2. Решая систему (1), найдём стационарные точки функции:
 Û
Û  Û
Û
Û  (2)
(2)
Первое уравнение системы (2) умножим на 7 и вычтем из второго: 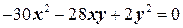 Û
Û
Û  . (3)
. (3)
Заметим, что y ¹0 (в противном случае из уравнения (3) получаем x =0, то есть имеем x =0 и y =0, что противоречит любому уравнению системы (2)). Разделим уравнение (3) на y 2:  , и сделаем замену
, и сделаем замену  . Приходим к уравнению
. Приходим к уравнению  , и решаем его:
, и решаем его:
D =142-4×15×(-1)=196+60=256=162,  ,
,  ,
, 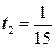 ,
,
то есть  или
или  . Дальше рассмотрим отдельно два случая:
. Дальше рассмотрим отдельно два случая:
Случай 1.  , то есть x =- y. Подставляя это равенство, например, в первое уравнение системы (3), получаем уравнение
, то есть x =- y. Подставляя это равенство, например, в первое уравнение системы (3), получаем уравнение 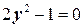 , решениями которого являются y 1, 2=
, решениями которого являются y 1, 2=  =
=  , откуда и x 1, 2=
, откуда и x 1, 2=  , и Х 1=(
, и Х 1=(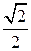 ,
,  ), Х 2=(
), Х 2=(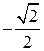 ,
, 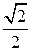 ) - стационарные точки.
) - стационарные точки.
Случай 2. 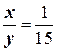 , то есть y =15 x. Подставляя это равенство в первое уравнение системы (3), получаем
, то есть y =15 x. Подставляя это равенство в первое уравнение системы (3), получаем
 Û
Û  Û x 3, 4=
Û x 3, 4=  ,
,
откуда y 3, 4