Если деформируемое тело имеет форму тела вращения, то можно воспользоваться условиями симметрии и несколько упростить общие уравнения теории упругости. Для такой упрощенной задачи имеется ряд решений, могущих иметь практическое значение.
С телами вращения часто приходится иметь дело в технических расчетах, но при определении напряжений и деформаций обыкновенно в таких случаях ограничиваются самыми грубыми приближенными решениями, для чего приводят задачу, при помощи различных допущений, к простейшему типу. Так, например, при расчете круглых цилиндрических брусков на растяжение и сжатие предполагают, что растягивающие или сжимающие напряжения авномерно распределены по концевым поперечным сечениям стержня, и приводят задачу к случаю однородного напряженного состояния. В случае конических стержней, подвергающихся действию растяжения или сжатия, предполагают во всяком поперечном сечении равномерное распределение нормальных напряжений. При расчете валов переменного поперечного сечения, работающих на кручение, обыкновенно исходят из распределения напряжений, найденного для круглого цилиндрического стержня и т. д.
Рис. 82.
Рис. 83.
В действительности перечисленные задачи значительно сложнее. Например, при растяжении стержня растягивающие силы 
(рис. 82) распределяются по закраинам 
и в поперечном сечении 
близком к головке растягиваемого бруска, распределение растягивающих напряжений будет далеко не равномерным.
При сжатии цилиндра между досками пресса 
и 
(рис. 83) по плоскостям соприкасания 
сжимающие напряжения также распределяются неравномерно. Кроме того, вследствие трения здесь получаются касательныенапряжения, препятствующие цилиндру свободно расширяться в поперечном направлении.
При скручивании вала переменного сечения (рис. 84) в переходном сечении 
распределение напряжений может значительно отличаться от линейного закона, найденного для круглых цилиндров, и перенапряжения
получаются тем большими, чем меньше радиус кривой, сопрягающей два участка вала различных диаметров.
При решении такого рода задач выгодно использовать условия симметрии. Мы выберем ось симметрии за одну из координатных осей, тогда соответствующей координатой будут определяться положения поперечных сечений тела, нормальных к оси вращения. Для определения положения точки в каком-либо определенном поперечном сечении удобнее всего в случае тел вращения воспользоваться полярными координатами. Если ось вращения назовем осью z, то величинами 
и 
вполне будет определяться положение точки тела.
Рис. 84.
При составлении дифференциальных уравнений равновесия мы воспользуемся результатами, полученными при решении плоской задачи в полярных координатах (§ 37). Напишем уравнения равновесия для бесконечно малого элемента (рис. 85), выделенного из тела двумя меридиональными плоскостями, двумя цилиндрическими поверхностями с радиусами 
и двумя поперечными сечениями, проведенными на расстоянии 
друг от друга. Кроме сил, которые мы принимали во внимание при решении плоской задачи, сюда войдут еще усилия по верхней и нижней граням выделенного элемента, перпендикулярным к оси z. Нормальные напряжения по этим граням обозначим через 
а касательные напряжения — через 
Проектируя все приложенные к элементу силы на направление радиуса, направление оси z и направление перпендикуляра к плоскости 
получаем таким же образом, как и в случае плоской задачи, следующие уравнения равновесия
Рис. 85.
Объемными силами мы при этом пренебрегаем.
Условия на поверхности (3) могут быть несколько упрощены, так как нормаль 
к поверхности тела вращения будет перпендикулярна к направлению напряжения 68. Отличными от нуля будут лишь 
Обозначая через 
проекции интенсивности поверхностного давления на направлении 
перепишем условия (3) в таком виде:
В дальнейшем мы ограничимся таким видом деформации тел вращения, при котором распределение напряжений не зависит от угла 6. В таком случае в уравнениях равновесия (100) пропадут все члены, в которые множителем входит производная по 0, и мы получим такую систему:
Первые два уравнения этой системы и первые два из условий (101) не заключают касательных напряжений 
и 
Соответствующее им распределение напряжений будет симметричным относительно оси вращения. По меридиональным сечениям будут действовать лишь нормальные напряжения 
Перемещения отдельных точек тела при такой деформации будут происходить в меридиональных сечениях.
В третье уравнение системы 102) и в третье из условий (101) входят лишь касательные напряжения 
Эти напряжения, как мы увидим далее, возникают при скручивании тела вращения.
Рассмотрим сначала случай симметричной деформации. При решении этой задачи можно идти двумя различными путями в зависимости от условий на поверхности. Если нам заданы перемещения точек поверхности, то удобнее выразить составляющие напряжения 
через перемещения. При заданных на поверхности напряжениях можно непосредственно приступить к определению напряжений из уравнений (102), но при этом нужно иметь в виду, что определяемое таким путем напряженное состояние должно удовлетворять дифференциальным зависимостям (40). Наметим общий ход решения задачи в обоих случаях.
Пусть 
обозначают перемещения какой-либо точки в направлении радиуса 
в направлении перпендикуляра к меридиональному сечению и в направлении оси z.
Тогда составляющие деформации представятся такими формулами (§ 37):
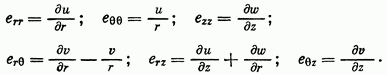
Пользуясь для объемного расширения обозначением 
получаем выражения для составляющих напряжения в таком виде (§ 17):
Вставляя эти значения напряжений в уравнения (102), получаем для симметричной деформации такие уравнения:
В эти уравнения входят два неизвестных перемещения 
Исключая одно из них, можно привести задачу к решению одного дифференциального уравнения четвертого порядка.
Для непосредственного определения напряжений выгодно в данном случае воспользоваться функцией напряжений. Оказывается, что первым двум уравнениям системы (102) можно удовлетворить, выражая все составляющие напряжения через одну функцию 
таким образом:
Здесь через 
обозначена операция 
соответствующая, в случае симметричной деформации, операции 
Для прямоугольной системы координат (§ 37).
Остается подобрать функцию 
так, чтобы были удовлетворены дифференциальные зависимости (40). Представим эти зависимости в цилиндрических координатах. Вместо составляющих напряжения 
придется воспользоваться их выражениями через 
. В таком случае
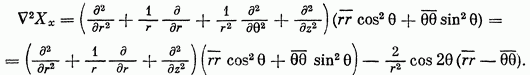
Кроме того, для симметричной деформации [формула (b) § 37] имеем
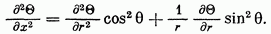
Вставляя это в первое из условий (40) и принимая во внимание, что уравнение должно быть удовлетворено при всяком угле 0, находим:
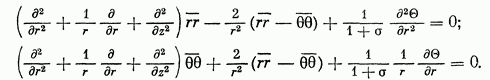
Эти два уравнения заменят нам первые два уравнения системы (40). Третье уравнение той же системы останется при переходе к цилиндрическим координатам без изменения.
Вместо трех последних уравнений системы (40), заключающих касательные напряжения, будем иметь в случае деформации, симметричной относительно оси, одно уравнение, которое легко может быть получено из уравнения четвертого или пятого системы (40).
Принимая во внимание, что
из уравнения пятого получаем
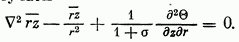
Такой же результат мы бы получили и из уравнения четвертого системы (40). Что касается уравнения шестого той же системы, то оно в рассматриваемом случае всегда будет удовлетворено.
Таким образом, дифференциальные зависимости (40) в случае деформации, симметричной относительно оси, могут быть представлены в таком виде:
Вставляя в эти уравнения выражения для напряжений (106), легко убедиться, что все они будут удовлетворены, если только функция напряжений 
удовлетворяет уравнению
Таким образом, решение задач теории упругости в случае симметричной деформации может быть приведено к интегрированию одного дифференциального уравнения (108) в частных производных четвертого порядка. При этом на поверхности должны быть удовлетворены уравнения (101).