ЛЕКЦИЯ № 7
Уравнение Шредингера
В общем случае поведение квантовой частицы описывается волновой функцией (амплитудой вероятности)
, (7-1)
которая является решением дифференциального волнового уравнения Шредингера
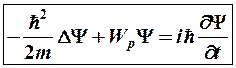, (7-2)
– общее (временнóе) уравнение Шредингера,
где m – масса частицы,
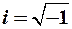– мнимая единица,
– оператор Лапласа.
Для стационарных полей, когда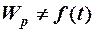 
(в одномерном случае)
.
Подставив это выражение в (7-2), после преобразований получим:
(7-3)
– уравнение Шредингера для стационарного поля.
Решением (7-3) является волновая функция
(7-4)
Для свободной частицы Wp = 0, тогда уравнение Шредингера примет вид:
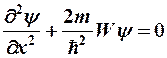
Обозначив 
(7-5)
,
где k - волновое число квантовой частицы,
получим
– однородное линейное дифференциальное уравнение второго порядка.
Решением этого уравнения является обычная гармоническая функция вида синуса или косинуса
,
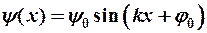при этом k – волновое число, а значит и импульс p, и энергия частицы W могут быть любыми!
Квантовая частица в одномерной
Бесконечно глубокой «потенциальной яме»
| I | II | III |
| Wp = ¥ | Wp = 0 | Wp = ¥ |
 y I = 0
| y II-? | y III = 0 |
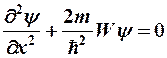или
Решением этого уравнения является
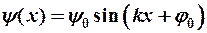
Но для х = 0 y (0) = 0, тогда j 0 = 0,
для х = 
y ( ) = 0, тогда sin(k ) = 0.
k = np, n = 1, 2, 3, ….
откуда
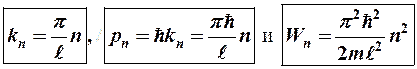(7-6)
где n = 1, 2, 3, ….
– квантование волнового числа, импульса и энергии частицы.
Значит поведение квантовой частицы в различных состояниях (с различными значениями kn, pn и Wn) будет описываться разными волновыми функциями
, n = 1, 2, 3, …. (7-7)
Воспользовавшись условием нормировки волновой функции
получим выражение для амплитуды y 0
Итак, квантовая частица – это волна - волна де Бройля. Но волна в ограниченной области пространства - это стоячая волна, для которой должно выполняться условие:
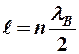
– условие квантования волн де Бройля.
Квантовый гармонический осциллятор
В твердом теле ионы находятся в узлах кристаллической решетки и совершают гармонические колебания у положения равновесия.
Поэтому эти микрочастицы также можно рассматривать в качестве квантовых гармонических осцилляторов, потенциальная энергия взаимодействия которых описывается выражением
.
Тогда подставляем это значение для Wp в уравнение Шредингера (7-3) и, решая его относительно энергии, получаем также, что энергия такой несвободной частицы не может быть любой, она квантуется:
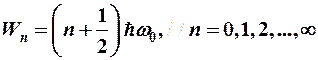, (7-8)
где 
– энергия нулевого состояния.
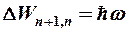
- уровни энергии располога-ются эквидистантно.
Влияние формы «потенциальной ямы»
на квантование энергии частицы
Энергия частицы складывается из энергии движения Wk и энергии взаимодействия Wp
W = Wk + Wp.
Если частица находится в «потенциальной яме», то Wk может переходить в Wp и наоборот.
, а т. к. частицы обладает волновыми свойствами, то по формуле де Бройля можно вычислить импульс этой частицы через ее длину волны.
.
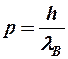Тогда 
.
Потенциальная энергия 
,
где 
g = 0, 
- свободная частица;
g = ¥, 
- прямоугольная бесконечно глубокая «потенциальная яма»;
g = 2, 
- гармонический осциллятор.
Для частицы в «потенциальной яме»
,
откуда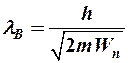 
откуда 
Так как частицу в «яме» можно считать стоячей волной, тогда можно воспользоваться условием:
, n = 0, 1, 2…
Тогда 
откуда 
Окончательно
1) g = 0 свободная частица; 
- любая;
2) g = ¥, 
- частица в бесконечно глубокой «потенциальной яме»;
, n = 1, 2…
3) g = 2, 
- квантовый гармонический осциллятор;
, n = 0, 1, 2…
4) g = -1, 
- электрон в атоме.
Т. о. форма потенциальной ямы очень сильно влияет на квантование энергии частицы.