1. Функция не может иметь более одного предела.
2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций.
3. Предел произведения конечного числа функций равен произведению пределов этих функций.
4. Предел постоянной величины равен этой постоянной.
5. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен 0).
6. Если  .
.
Виды неопределенностей
 .
.
!!! Основной задачей при вычислении пределов является устранение неопределенностей с помощью алгебраических преобразований.
1) для неопределенности вида 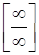 :
:
- Если в числителе и знаменателе сложные степенные или показательные функции и  . Вычисление пределов в случае отношения степенных функций производится путем вынесения за скобку в числителе и знаменателе дроби переменной x в наибольшей степени среди всех слагаемых дроби (неопределенность устраняется после сокращения дроби и применения основных теорем о пределах); в случае показательных функций за скобку выносится наибольшее слагаемое.
. Вычисление пределов в случае отношения степенных функций производится путем вынесения за скобку в числителе и знаменателе дроби переменной x в наибольшей степени среди всех слагаемых дроби (неопределенность устраняется после сокращения дроби и применения основных теорем о пределах); в случае показательных функций за скобку выносится наибольшее слагаемое.
- Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле, т.е.
 .
.
2) для неопределенности вида 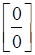 :
:
- Если возможно, то числитель и знаменатель разложить на множители. Неопределенность устраняется после сокращения дроби.
- Числитель и знаменатель дроби домножить на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
Формулы сокращенного умножения:
(a-b)(a+b)= a2-b2
(a-b)(a2+ab+b2)=a3-b3
- Правило Лопиталя.
3) для неопределенности вида [0  ]:
]:
- Выражение, представляющее собой произведение функций, нужно преобразовать в частное (не меняя смысла). После чего неопределенность преобразуется к виду 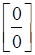 или
или 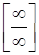 .
.
4) для неопределенности вида [  ]:
]:
- Если функция, стоящая под знаком предела, представляет собой сумму или разность дробей, то неопределенность или устраняется, или приводится к типу 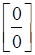 после приведения к общему знаменателю.
после приведения к общему знаменателю.
- Если функция, стоящая под знаком предела, представляет собой разность или сумму иррациональных выражений, то неопределенность или устраняется, или приводится к типу 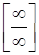 путем домножения и деления функции на одно и то же выражение, приводящее к формулам сокращенного умножения.
путем домножения и деления функции на одно и то же выражение, приводящее к формулам сокращенного умножения.
5) для неопределенности вида [ 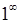 ]:
]:
- Выражение, стоящее под знаком предела представляет собой степенно-показательную функцию (в основании которой необходимо выделить целую часть дроби). Неопределенность устраняется при помощи выделения второго замечательного предела.
Формула второго замечательного предела:
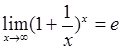 ;
; 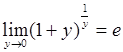 .
.
ПРОИЗВОДНАЯ
Определение: Производной функции y=f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к 0 (если этот предел существует):

Если функции u(x) и v(x) дифференцируемые, то справедливы следующие правила дифференцирования:
(u+v)¢=u¢+v¢
(u-v)¢=u¢-v¢
(uv)¢=u¢v+uv¢
(cu)¢=cu¢
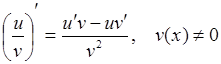
Производные основных элементарных функций:
(c)¢=0; (x)¢=1
| простые | сложные |
степенная

| степенная (un)¢=nun-1u¢ |
| показательная (ex)¢= ex (ax)¢=axlna | показательная (eu)¢= euu¢ (au)¢=aulna*u¢ |
логарифмическая
(ln x)¢=  (logax)¢=
(logax)¢= 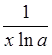
| логарифмическая
(ln u)¢=  (logau)¢=
(logau)¢= 
|
тригонометричекая
(sin x)¢=cos x
(cos x)¢=-sin x
(tg x)¢=  (ctg x)¢=
(ctg x)¢= 
| тригонометричекая
(sin u)¢=cos u*u¢
(cos u)¢=-sin u*u¢
(tg u)¢= 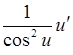 (ctg u)¢=
(ctg u)¢= 
|
СУММЫПРОГРЕССИЙ,
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Арифметическая прогрессия
 ,где d – разность;
,где d – разность;
 .
.
Геометрическая прогрессия
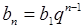 ;
;
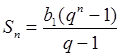 .
.
Бесконечно убывающая геометрическая прогрессия
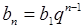 ;
;
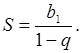
Значения тригонометрических функций
| a | p/6 (30°) | p/4 (45°) | p/3 (60°) | p/2 (90°) | 2p/3 (120°) | 3p/4 (135°) | 5p/6 (150°) | p (180°) | |
| sina | 1/2 |  /2 /2
|  /2 /2
|  /2 /2
|  /2 /2
| 1/2 | |||
| cosa |  /2 /2
|  /2 /2
| 1/2 | -1/2 | -  /2 /2
| -  /2 /2
| -1 | ||
| tga |  /3 /3
| 
| - | - 
| -1 | -  /3 /3
| |||
| ctga | - | 
|  /3 /3
| -  /3 /3
| -1 | - 
| - |
| a | 7p/6 (210°) | 5p/4 (225°) | 4p/3 (240°) | 3p/2 (270°) | 5p/3 (300°) | 7p/4 (315°) | 11p/6 (330°) | 2p (360°) |
| sina | -1/2 |  /2 /2
|  /2 /2
| -1 | -  /2 /2
| -  /2 /2
| -1/2 | |
| cosa | -  /2 /2
|  /2 /2
| 1/2 | 1/2 |  /2 /2
|  /2 /2
| ||
| tga |  /3 /3
| 
| - | - 
| -1 | -  /3 /3
| ||
| ctga | 
|  /3 /3
| -  /3 /3
| -1 | - 
| - |
ИССЛЕДОВАНИЕ ФУНКЦИИ y=f(x) И ПОСТРОЕНИЕ ЕЕ ГРАФИКА
Схема исследования:
1. Найти область определения функции (ООФ – значения переменной х, при которых функция существует).
2. Исследовать функцию на четность – нечетность:
Если f(-x)=f(x), то функция четная (график симметричен относительно оси О y).
Если f(-x)=-f(x), то функция нечетная (график симметричен относительно начала координат).
3. Найти вертикальные асимптоты.
!!! Вертикальные асимптоты х=х0 следует искать в точках разрыва функции y=f(x) или на концах ее области определения (a,b), если a и b - конечные числа.
Пусть функция y=f(x) определена в некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х®х0-0 (слева) или х®х0+0 (справа) – равен бесконечности, т.е. lim f(x)=  или lim f(x)=
или lim f(x)=  . Тогда прямая х=х0 является вертикальной
. Тогда прямая х=х0 является вертикальной
х®х0-0 х®х0+0
асимптотой графика функции y=f(x).
4. Найти горизонтальные асимптоты (исследовать поведение функции в бесконечности).
Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции lim f(x)=b.
Тогда прямая y=b есть Х 
горизонтальная асимптота графика функции y=f(x).
Замечание. Если конечен только один из пределов lim f(x)=bл
или Х 
lim f(x)=bп, то функция имеет левостороннюю y=b л
или правостороннюю Х 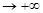
y=bп горизонтальную асимптоту.
5. Найти наклонную асимптоту.
Пусть функция y=f(x) определена при достаточно больших х и существуют конечные пределы функции lim  и lim[f(x)-kx]=b
и lim[f(x)-kx]=b
Х 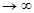 Х
Х 
Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(x).
!!! Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней.
6. Найти экстремумы (максимум, минимум) и интервалы монотонности (возрастание, убывание) функции.
- найти производную функции (разложить ее на множители) и приравнять ее к 0, т.е. 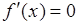 ;
;
- найти корни этого уравнения и точки, в которых производная не существует (критические точки);
- исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции (найти ординаты точек экстремума!);
- на промежутке, где  - функция возрастает; на промежутке, где
- функция возрастает; на промежутке, где  - функция убывает.
- функция убывает.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
!!! Уравнение оси Ох: y=0.
Уравнение оси Oy: х=0.
8. Используя результаты исследования, построить график функции.