Если метод сходится, то есть  , где
, где
 – точное решение
– точное решение
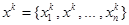 – k-тое приближение к точному решению, то итерационный процесс следовало бы закончить по достижению заданной погрешности
– k-тое приближение к точному решению, то итерационный процесс следовало бы закончить по достижению заданной погрешности  , где e – заданная точность (погрешность).
, где e – заданная точность (погрешность).
Однако практически это условие выполнить нельзя, так как 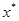 неизвестно, тогда для окончания итерационного процесса можно воспользоваться неравенствами
неизвестно, тогда для окончания итерационного процесса можно воспользоваться неравенствами 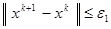 , или
, или 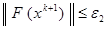 , где
, где 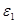 и
и  – заданные величины.
– заданные величины.
При таком окончании итераций погрешность может возрасти по сравнению с  и, поэтому, чтобы не увеличивалась, величины
и, поэтому, чтобы не увеличивалась, величины  и
и 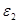 соответственно уменьшают или увеличивают число итераций.
соответственно уменьшают или увеличивают число итераций.
Методы простой итерации, Зейделя, модифицированный метод Ньютона, метод наискорейшего спуска (см. [1], [2], [3], [4]) являются методами первого порядка – это значит, что имеет место неравенство 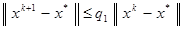 , k =1, 2,..., где
, k =1, 2,..., где  – константа, своя у каждого метода, зависящая от выбора начального приближения
– константа, своя у каждого метода, зависящая от выбора начального приближения  , функции fi, i = 1, 2,..., n, и их частных производных первого и второго порядков – точнее их оценок в некоторой окрестности искомого решения, которой принадлежит начальное приближение.
, функции fi, i = 1, 2,..., n, и их частных производных первого и второго порядков – точнее их оценок в некоторой окрестности искомого решения, которой принадлежит начальное приближение.
Метод Ньютона является методом второго порядка, то есть для него имеет место неравенство  , k =1, 2,..., где
, k =1, 2,..., где  – константа, зависящая от тех же величин, что и константа
– константа, зависящая от тех же величин, что и константа  .
.
А теперь рассмотрим достаточные условия сходимости метода простой итерации и метода Ньютона.
Сходимость процесса простой итерации зависит от двух условий. Первое условие состоит в том, что какая-нибудь точка 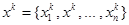 должна оказаться близкой к исходному решению
должна оказаться близкой к исходному решению 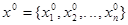 . Степень необходимой близости зависит от функций j1 , j2,..., jn. Это требование не относится к системам линейных уравнений, для которых сходимость процесса простой итерации зависит только от второго условия.
. Степень необходимой близости зависит от функций j1 , j2,..., jn. Это требование не относится к системам линейных уравнений, для которых сходимость процесса простой итерации зависит только от второго условия.
Второе условие связано с матрицей, составленной из частных производных первого порядка функций j1 , j2,..., jn – матрицей Якоби
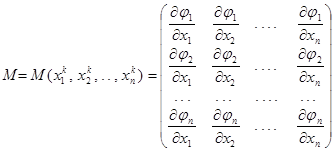 ,
,
вычисленных в точке 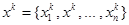 .
.
В случае, когда рассматривается система линейных алгебраических уравнений, матрица M состоит из постоянных чисел – коэффициентов, стоящих при неизвестных в правой части уравнения (3). В случае нелинейных уравнений элементы  матрицы M зависят, вообще говоря, от
матрицы M зависят, вообще говоря, от 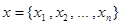 . Для сходимости процесса простой итерации достаточно, чтобы выполнялось неравенство:
. Для сходимости процесса простой итерации достаточно, чтобы выполнялось неравенство:  для
для 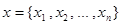 из некоторой окрестности точного решения
из некоторой окрестности точного решения 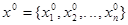 , которой должно принадлежать начальное приближение
, которой должно принадлежать начальное приближение 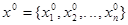 .
.
Приведем также достаточные условия сходимости метода Ньютона для системы уравнений вида (2) по норме 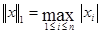 .
.
Предположим, что имеется начальное приближение  к искомому решению системы (2)
к искомому решению системы (2) 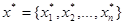 , функции
, функции 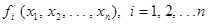 непрерывны и имеют непрерывные частные производные до второго порядка в шаре
непрерывны и имеют непрерывные частные производные до второго порядка в шаре 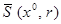 , тогда, если выполнены условия:
, тогда, если выполнены условия:
1) Матрица Якоби  системы (2) на начальном приближении имеет обратную
системы (2) на начальном приближении имеет обратную 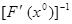 и известна оценка нормы обратной матрицы
и известна оценка нормы обратной матрицы  ,
,
2) Для всех точек шара 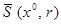 выполнено неравенство
выполнено неравенство
 при i, j = 1, 2,..., n,
при i, j = 1, 2,..., n,
3) Выполнено неравенство
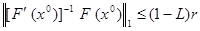 ,
,
где L – постоянная 0 £ L £ 1,
4) Числа b, N, r подчинены условию a = nbNr < 0,4, тогда система уравнений (2) в шаре 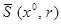 имеет единственное решение, к которому сходятся последовательные приближения (8) или (7’), (9’).
имеет единственное решение, к которому сходятся последовательные приближения (8) или (7’), (9’).
Для других методов условия сходимости имеют сложный вид, и мы отсылаем читателя к специальной литературе [1], [2], [3], [4].