Лекция 1. Физическое явление и его математическая модель. Требования, предъявляемые к математической модели. Математические модели и численные методы. Преимущества вычислительных методов перед аналитическими. Понятия о корректной постановке задачи. Структура погрешности решения
Математическое моделирование – это современная технология изучения физических явлений и проектирования сложных технических систем с помощью представления наиболее существенных свойств объекта моделирования на языке математических понятий и уравнений.
Математическая модель, основанная на некотором упрощении, идеализации, не тождественна объекту, а является его приближенным описанием. Однако, благодаря замене реального объекта соответствующей моделью появляется возможность сформулировать задачу его изучения как математическую и воспользоваться для анализа универсальным математическим аппаратом, который не зависит от конкретной природы объекта. Математика позволяет единообразно описать широкий круг фактов и наблюдений, провести их детальный количественный анализ, предсказать, как поведет себя объект в различных условиях, то есть спрогнозировать результаты будущих наблюдений.
Основные задачи, решаемые с помощью математического моделирования это
– оптимальное проектирование многомерных объектов (мультидисциплинарная оптимизация),
– замена физического эксперимента вычислительным с высокой разрешающей способностью в пространстве и времени.
Примером первой задачи может быть оптимальное проектирование охлаждаемой рабочей лопатки турбины. Эта задача решается с помощью комплекса математических моделей (геометрической, аэродинамической, теплопроводности, напряженно-деформированного состояния) различного уровня. Следует отметить неизбежный итерационный характер решения этой задачи, возникающий в результате уточнения параметров на каждом этапе использования моделей более высокого уровня.
Примером второй задачи, непосредственно связанной с первой, является
Моделирование нестационарного обтекания рабочей лопатки турбины. Здесь мы в каждый момент времени имеем полную информацию о кинематическом (поле скоростей), силовом (поле давлений) и температурном состоянии потока вокруг лопатки турбины при ее движении относительно неподвижных лопаток соплового аппарата. Физический эксперимент в его наиболее существенной (детерминированной) части заменяется здесь вычислительным.
Математические модели существенным образом различаются по типу уравнений. Принято классифицировать модели по уровню описания физических явлений.
Модель первого уровня – это простой функциональный оператор вида 
. Поскольку в этом операторе отсутствуют уравнения физических законов сохранения массы, энергии и импульса, то иногда модель такого типа называют «черным ящиком», входом в который является аргумент или вектор X, а выходом функция или вектор Y. В общем случае модель первого уровня аппроксимируется полиномом и поэтому она также может быть названа аппроксимационной моделью. По существу любая аппроксимация экспериментальных данных является моделью первого уровня. Несмотря на ограниченность применения моделей первого уровня, некоторые из них могут иметь высокий уровень обобщения. Например, зависимость безразмерного коэффициента теплоотдачи в гладких каналах от гидравлического режима течения (
) является достаточно фундаментальным обобщением экспериментальных данных настолько, что не имеет смысла получать эту зависимость с помощью решения уравнений в частных производных.
Модель второго уровня (термодинамическая, или в сосредоточенных параметрах) содержит в себе уравнения сохранения или является их решением. Например, выражение для адиабатической работы турбины 
, которое также может быть аппроксимировано полиномом или получено в эксперименте, является решением стационарного уравнения сохранения энергии в адиабатическом процессе расширения газа. Аналогичные модели используются для одномерного термодинамического и газодинамического расчета процессов в авиационном двигателе.
Модель третьего уровня описывает систему с распределенными параметрами в пространстве и в общем случае во времени. Соответственно уравнения модели это дифференциальные уравнения в частных производных. Например, система уравнений Эйлера для идеального газа или Навье – Стокса для вязкого совершенного ньютоновского газа. Решение этой системы уравнений при заданных граничных условиях может быть получено как аналитически (в наиболее простых случаях), так и численными методами.
Рассматривая математический анализ явления как своего рода теоретический эксперимент, из общих и достаточно естественных соображений процесс математического моделирования разбивается на несколько этапов:
- Формулировка математической модели явления. Математическая модель явления, по причине его чрезвычайной сложности, должна охватывать важнейшие для рассматриваемой задачи стороны процесса, его существенные характеристики и формализованные связи, подлежащие учету. Как правило, математическая модель изучаемого физического явления формулируется в виде уравнений математической физики. На этой стадии анализа это существенно нелинейные, многомерные системы уравнений, содержащие большое число неизвестных параметров.
Если математическая модель выбрана недостаточно тщательно, то какие бы мы не применяли методы для дальнейших расчетов, полученные результаты будут ненадежны, а в отдельных случаях и совершенно неверны.
- Проведение математического исследования полученной модели и получение соответствующего решения. На этом этапе моделирования, в зависимости от сложности рассматриваемой модели, применяют различные подходы к ее исследованию, и различный смысл вкладывается в понятие решения задачи.
Для наиболее грубых и несложных моделей удается получить их аналитическое решение. Для более точных и сложных моделей аналитическое решение удается получить сравнительно редко. При теоретическом анализе задачи в такой ситуации воспользуемся приближенными математическими методами, например разложением по малому параметру, осреднением, изучением различных асимптотик и другими. Эти приемы позволяют опять таки представить приближенное решение в аналитической форме и с его помощью получить удовлетворительные численные результаты.
Наконец, для более точных и сложных моделей основными методами решения являются численные методы решения с необходимостью требующие проведения большого объема вычислений на ЭВМ. Эти методы позволяют добиться хорошего количественного и даже качественного результата в описании модели в условиях, максимально приближенных к реальным – в условиях сложной геометрии пространства протекания физического явления, многообразия протекающих процессов, что делает результаты практически значимыми. В этом состоит их преимущество перед традиционными – аналитическими и приближенными методами. Но правда у них есть и принципиальные недостатки – как правило, речь идет о рассмотрении некоторого конкретного решения.
Приведенная на рис. 1 схема частично отражает обсуждаемые взаимосвязи этапов математического моделирования.
Рис. 1. Схема взаимосвязи этапов математического моделирования
- Анализ состоятельности предложенной модели, то есть осмысление результатов решения, сопоставление полученного решения с имеющимися данными физического эксперимента. На этом этапе решается вопрос о состоятельности математической модели и проведенного исследования. «Хорошее» согласование с «экспериментом» обычно свидетельствует о правильности выбора модели. В противном случае необходимы дополнительные уточнения, изменения и так далее, повторение предыдущих этапов исследования.
Использование ЭВМ в процессе математического исследования модели требует специфических численных методов, то есть такой интерпретации математической модели, которая может быть реализована на ЭВМ – назовем ее дискретной или вычислительной моделью. Поскольку ЭВМ выполняет только арифметические и логические операции, то для реализации вычислительной модели требуется разработка соответствующего вычислительного алгоритма. Дальнейшая последовательность действий – это программирование, расчет на ЭВМ, обработка результатов расчета.
Остановимся на отдельных проблемах численных методов.
Понятие о корректно поставленной задаче.
Обычно задачу вычисления величины у по известной величине х записывают, с учетом интересующих нас причинно-следственных связей, в виде
, (1)
где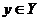 
, 
– элементы соответствующих функциональных пространств, А – оператор (правило), реализующий вычисления.
Задача вычисления называется корректно поставленной, если для любых входных данных из некоторого класса решение задачи существует, единственно и устойчиво по входным данным (то есть непрерывно зависит от входных данных задачи).
В сформулированном понятии корректности поставленной задачи (по Адамару) учтены достаточно естественные требования, действительно: чтобы численно решать задачу нужно быть уверенным, что ее решение существует. Столь же разумны для конкретных условий и требования единственности решения, и, поскольку наши действия носят принципиально приближенный характер, то необходимо требование устойчивости решения. Эти вопросы будут рассмотрены в специальных разделах курса.
Численное решение корректных задач. Структура погрешности решения.
Есть четыре основных источника погрешности результата вычислений: 
–математическая модель; 
– исходные данные задачи; 
– приближенный метод решения; 
–погрешность при реализации вычислений (в частности погрешность округления):
– Погрешность математической модели связана с физическими допущениями при выборе математической модели, на анализе этой погрешности мы останавливаться не будем.
– Погрешность исходных данных порождает неустранимую погрешность решения
.
– Погрешность метода связана с тем, что выражение 
, вообще говоря, не может быть непосредственно численно реализовано. Поэтому задачу заменяют «близкой» задачей 
. Мы переходим к другим функциональным пространствам 
, элементы которых допускают сравнительно «простую» численную реализацию. При этом естественно потребовать, чтобы новая задача была корректной, и ее решение было близко к решению исходной задачи. Величина
и представляет собой погрешность метода.
– Вычислительная погрешность связана с округлением промежуточных результатов при расчете на ЭВМ. Она может быть записана в виде
.
Вычислительная погрешность напрямую связана с понятием устойчивости алгоритма, которое будет обсуждаться далее в разделах курса.
Полезно сразу же сформулировать некоторые эмпирические правила, которых придерживаются при реализации задачи вычисления:
.
1) При проведении вычислений нужно стремиться, чтобы погрешность метода была бы в несколько раз меньше неустранимой погрешности решения .
2) Вычислительная погрешность должна быть существенно меньше всех.