Операции над множествами.

Определим операции над множествами, с помощью которых можно строить новые множества из уже имеющихся множеств.

Объединением множеств A и B называется множество, обозначаемое , состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В. Символически это можно записать так:

.

Рассмотрим пример.

Пусть , , тогда .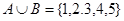

Пересечением множеств А и В, обозначение 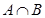, называется множество, состоящее из всех тех и только тех элементов, которые принадлежат и А, и В.

.

Для нашего примера .

Операции объединения и пересечения позволяют обобщение: можно рассматривать объединение и пересечение совокупности множеств.

Разностью множеств А и В, обозначение А\ В (А - В), называется множество всех тех и только тех элементов А, которые не принадлежат B.

.

Соответственно, .

Для нашего примера: A\B= {1, 2}, B\A= {4, 5}.

Симметрической разностью множеств А и В, обозначение , называется множество всех тех и только тех элементов, которые либо принадлежат А и не принадлежат B, либо принадлежат B, но не принадлежат A.

.

Для симметрической разности справедливы соотношения:

.

.

Для наших множеств .

Если все рассматриваемые множества являются подмножествами некоторого универсального множества U, то может быть определена операция дополнения.

Дополнением (до U) множества А, обозначение ,называется множество всех элементов U, не принадлежащих A. Множество U должно быть либо задано, либо очевидно из контекста.

.

Определим для наших множеств A и B универсум: U = {1, 2,…, 8}. Тогда , .

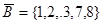Операции над множествами удобно изображать графически. Универсальное множество изображается в виде прямоугольника. Сами исходные множества изображаются фигурами внутри прямоугольника (кругами или овалами), а результат операций графически выделяется, закрашивается. Такие диаграммы называются диаграммами Эйлера-Венна. Например, диаграммы операций пересечения, объединения и разности двух множеств выглядят следующим образом:

Рис. 1. 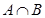Рис. 2. . Рис. 3.

Диаграммы для трех множеств A, B и C рисуются аналогичным образом.

На рисунках 4 и 5 изображены результаты соответствующих операций над тремя множествами.

Рис. 4. Рис. 5.

Для мощности объединения двух множеств имеет место следующая формула, называемая формулой включений и исключений:

.

Для n конечных множеств формула принимает вид:

Рассмотрим задачу на применение этой формулы.

Предположим, что из 100 (универсум) опрошенных студентов 50 изучают химию (множество A), 53 (множество B) - математику, 42 (множество С) - физику, 15 - химию и физику (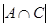), 20 занимаются физикой и математикой (), 25 - математикой и химией () и 5 студентов () изучают все три предмета. Требуется ответить на следующие вопросы.

a) Сколько студентов изучают хотя бы один из трех перечисленных предметов?

b) Сколько студентов не изучают ни один из трех перечисленных предметов?

c) Сколько студентов изучают только математику?

d) Сколько студентов изучают физику или химию, но не изучают математику?

e) Сколько студентов не изучают ни математику, ни химию?

Чтобы ответить на первый вопрос, нам необходимо найти мощность множества . Применим формулу включений и исключений:

.

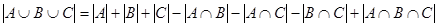Имеем:

.

Заметим, что, например, в число 15 студентов, изучающих химию и физику, входят 5 студентов, изучающих еще и математику. Поэтому, число студентов, изучающих только химию и физику равно: 15 – 5 = 10.

Аналогично, в число 50 студентов, изучающих химию, входят 10 студентов, изучающих только химию и физику, 20 студентов (25 – 5 = 20), изучающих только химию и математику, 5 студентов, изучающих все три предмета и, наконец, 15 студентов (50 – 10 – 20 – 5 = 15) изучают одну химию.

Чтобы найти число студентов, не изучающих ни один из трех предметов, необходимо от универсума отнять число студентов, изучающих хотя бы один предмет: 100 – 90 = 10.

Отвечаем на третий вопрос. Математику изучают 53 студента. Чтобы найти число студентов, изучающих только математику, необходимо от этого числа отнять число студентов, изучающих только математику и физику, только математику и химию и изучающих все три предмета.

Только математику и физику изучают: 20 – 5 = 15.

Только математику и химию: 25 – 5 = 20. Все три предмета изучают 5 студентов.

И для числа студентов, изучающих только математику, имеем: 53 – 15 – 20 – 5 = 13.

Найдем теперь, сколько студентов изучают физику или химию, но не изучают математику. Для этого сначала найдем число студентов, изучающих физику или химию по формуле для мощности объединения двух множеств:

.

Теперь от этого числа надо отнять число студентов, изучающих только химию и математику, только математику и физику и изучающих все три предмета. В результате имеем:

77 – 20 – 15 – 5 = 37.

Число студентов, не изучающих ни математику, ни химию, найдем, отняв от общего числа студентов число студентов, изучающих математику или химию. В результате имеем: 100 – 78 = 22.

Эту же задачу можно решить диаграммами Эйлера-Венна.

Диаграмма Эйлера-Венна приведена на рисунке 6. Как мы видим из диаграммы, универсум, включая множества A, B и C разбит на непересекающиеся между собой множества.

Рис. 6.

Пусть A, I – непустые множества и 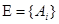– некоторое семейство непустых подмножеств множества (множество подмножеств A) A: , где множество I – множество индексов. Семейство называется разбиением множества A, если выполнены два условия:

1. ;

2. .

Множества при этом называются блоками разбиения множества A.

Например, на рисунке 7 условно изображено некоторое множество A, разбитое на пять блоков:

Рис. 7.

Пусть задано множество A = {1,2,3}. Имеем пять разбиений множества A:

, , , , .

Число всех разбиений n - элементного множества называется числом Белла и обозначается . В нашем случае n = 3 и .

Семейство называется покрытием множества A, если каждый элемент A принадлежит хотя бы одному из подмножеств : .

Для нашего множества A = {1,2,3} покрытиями будут являться, например, семейства: или .

Семейство называется дизъюнктным, если элементы этого семейства попарно не пересекаются, то есть каждый элемент множества A принадлежит не более чем одному из множества : . Семейство для нашего примера является дизъюнктным.

Как видим, разбиение множества A можно определить как дизъюнктное покрытие этого множества.