Кодирование числовой информации по сути представляет собой переход к записи в двоичной системе счисления чисел, записанных в общепринятой десятичной системе счисления. В этом случае двоичную форму записи десятичного числа можно назвать его двоичным кодом. Всякое десятичное число, прежде чем оно попадает в память компьютера для обработки, преобразуется в его двоичный эквивалент, а полученный результат, прежде чем мы увидим его на экране видеотерминала или на бумаге после печати, переводится из двоичной системы счисления в десятичную. Преобразование это происходит автоматически с помощью специальных программ (например, трансляторов). Однако чтобы лучше понять, как хранится, обрабатывается и отображается числовая информация в компьютере, надо научиться переводить числа из произвольной системы счисления в двоичную и наоборот, т.е. кодировать и декодировать числовую информацию.
Из многих вопросов, возникающих при изучении позиционных систем счисления, рассмотрим проблему замены целых чисел и правильных дробей какой-либо системы счисления с основанием р равными числами системы счисления с основанием q.
Как известно, одно и тоже число Z как количественная мера может быть представлена в различных позиционных системах счисления. Пусть некоторое целое число Z в системе счисления с основанием р имеет вид:
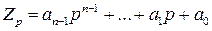 , (2.13)
, (2.13)
это же число в системе счисления с основанием q будет иметь другой вид
 , (2.14)
, (2.14)
где п и т – число разрядов, необходимое для записи числа Z соответственно в p -ичной и q -ичной системах счисления, 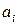 и
и  (
( ,
,  ) – веса разрядов.
) – веса разрядов.
При этом
 ,
,
 ,
,
где  и
и  –алфавиты соответствующих систем счисления.
–алфавиты соответствующих систем счисления.
Под переводом чисел из одной системы счисления в другую понимается определение его записи Zq в новой системе счисления с основанием q по известной записи Zp данного числа в исходной системе счисления с основанием р. Сокращенно это записывается в виде отображения
 . (2.15)
. (2.15)
Алгоритмы перевода чисел из одной системы счисления в другую базируются на известных положениях теории чисел, о которых далее будет вкратце сказано. Для простоты ограничимся рассмотрением процедуры перевода целых чисел.
Так, если даны два целых положительных числа Z и Р, записанных в одной и той же системе счисления, причем
Z=aP+b, (2.16)
то справедливы следующие соотношения
a=Z div P, (2.17)
b=Z mod P, (2.18)
где div – операция нахождения целой части числа, получаемого от деления двух целых чисел; (остаток отбрасывается), mod – операция выделения остатка от деления двух целых чисел (целая часть отбрасывается).
Соотношения (2.16) – (2.18) можно использовать для перевода двухзначных (двухразрядных) чисел из одной системы счисления в другую (см. формулу (2.15)). Будем рассматривать число Р в качестве основания системы счисления, в которой представлено число Z, т.е. положим р=Р, и Z 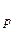 =Z=a*p+b, где а и b – соответственно старший и младший разряды исходного двухразрядного числа Zp.
=Z=a*p+b, где а и b – соответственно старший и младший разряды исходного двухразрядного числа Zp.
Для записи числа Zp в новой системе с основанием q нужно определить коэффициенты (цифры соответствующих разрядов нового числа)  ,
,  , .., такие, что
, .., такие, что
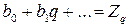 ,
,
при этом должно выполняться равенство:  .Заметим, что количество разрядов искомого числа заранее не известно.
.Заметим, что количество разрядов искомого числа заранее не известно.
С учетом (2.17), (2.18) коэффициенты  ,
,  , …найдутся из следующих соотношений:
, …найдутся из следующих соотношений:
 ,
,
 ,
,
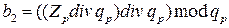 , (2.19)
, (2.19)
 ,
,
и т.д.
где qp есть запись q в системе счисления с основанием р.
Вычисления заканчиваются тогда, когда последовательное п- кратное применение операции div к числу Zp дает в результате 0, т.е.
 .
.
В этом случае 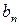 является цифрой старшего разряда искомого числа Zq и определяется из выражения:
является цифрой старшего разряда искомого числа Zq и определяется из выражения:
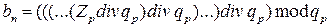 . (2.20)
. (2.20)
Соотношения (2.19), (2.20) остаются справедливыми и для случая перевода n -разрядного числа Zp в другую систему счисления. Формулами (2.19), (2.20) можно пользоваться как при переводе числа из системы счисления с большим основанием в систему счисления с меньшим основанием (p>q), так и при переводе числа из системы счисления с меньшим основанием в систему счисления с большим основанием (p<q). Иными словами, формулы (2.19), (2.20) являются универсальными формулами перевода чисел из одной системы счисления в другую. На этих формулах базируется так называемый алгоритм последовательного деления.
Проиллюстрируем применение универсальной схемы перевода (формулы (2.19) - (2.20)) на примере перевода числа из пятеричной системы счисления в четверичную и наоборот ( и
и  ).
).
Пример 1. Пусть Z5=435, для перевода этого числа в четверичную систему будем делить его на 45 с использованием правил арифметических действий в пятеричной системе. На рис. 2.3 представлена графическая схема данной процедуры, позволяющая наглядным способом получить цифры всех разрядов искомого числа.

Рис.2.3. Графическая схема алгоритма последовательного деления
Согласно этой схеме исходное число 435 делится на основание системы счисления, в которую переводится число (45). Полученный остаток после первого деления есть младший разряд нового числа (35). Образовавшееся частное (105) снова делится на это основание. Из остатка получили следующий разряд нового числа (15). Последнее частное от деления будет старшим разрядом искомого числа (т.к. 15 mod 45=15, 15 div 45=0). Стрелкой показано направление убывания разрядов искомого числа при его записи в позиционных системах счисления (слева направо). Двигаясь по стрелке, получим искомое число Z4 =1134.
Рассмотрим теперь обратный перевод полученного числа Z4=1134 в пятеричную систему счисления. Для этого сначала перед делением число 5 запишем в четверичную систему счисления (5=104), а затем воспользуемся так же, как в предыдущем примере универсальной схемой перевода:

Двигаясь по стрелке, получим числа искомого числа в четверичной системе в порядке убывания разрядов: 114, 34. Переводя эти числа в пятеричную систему счисления (114=45, 34=35), получим искомое число Z5=435.
Особенно удобно пользоваться данным алгоритмом при переводе числа из десятичной системы счисления, т.е. при переводе  ,при этом q может быть как больше, так и меньше 10. В этом случае деление производится в привычной нам десятичной системе счисления. Например, воспользуемся этим способом для перевода десятичного числа 263810 в шестнадцатеричную систему счисления:
,при этом q может быть как больше, так и меньше 10. В этом случае деление производится в привычной нам десятичной системе счисления. Например, воспользуемся этим способом для перевода десятичного числа 263810 в шестнадцатеричную систему счисления:
 (старший разряд целой части)
(старший разряд целой части)
Для описания алфавита шестнадцатеричной системы счисления возникает проблема нехватки имеющихся в распоряжении десяти арабских цифр, поэтому шестнадцатеричный алфавит дополняют прописными буквами А, В, С, D, E,F латинского алфавита, при этом, А=10, В=11, С=12, D=13, E=14, F=15. В приведенном выше примере число 14 заменим шестнадцатеричной цифрой Е, 10 - шестнадцатеричной цифрой А, получим 263810=A4E16.
Следует отметить, что, несмотря на возможность использования одного универсального алгоритма перевода чисел, на практике в дополнение к нему (особенно при p<q, т.к. в этом случае алфавит системы счисления с основанием р входит как подмножество в алфавит системы счисления с основанием q) применяется еще один алгоритм! основанный на следующей формуле:
 . (2.21)
. (2.21)
Достоинством этого алгоритма является отсутствие промежуточной процедуры перевода цифр искомого числа в нужную систему счисления.
Пример 2. Переведем с помощью данного алгоритма число Z4=1134 в пятеричную систему счисления. Выполнив согласно формуле (2.21) все необходимые действия в пятеричной системе счисления, получим запись искомого числа:
 .
.
Сравнивая процедуры перевода числа 1134 в пятеричную систему счисления, можно увидеть, что при совпадении результатов (Z5=435) во втором примере не было необходимости в предварительном переводе цифр исходного числа 1134 в пятеричную систему счисления.
Особенно удобно пользоваться данным алгоритмом при переводе числа в привычную для нас десятичную систему счисления, т.е. при переводе 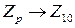 , при этом р может быть как больше, так и меньше 10.
, при этом р может быть как больше, так и меньше 10.
Например, перевод восьмеричного числа 3248 и шестнадцатеричного числа A9F16 в десятичную систему счисления производится очень просто:
 ,
,
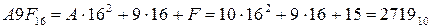 .
.
Отметим, что при использовании универсального алгоритма необходимо хорошее знание таблицы умножения в системах счисления с «непривычным» основанием (например, четверичной, пятеричной), что вызывает трудности, особенно при «ручном» переводе чисел. Поэтому на практике для перевода чисел «вручную» используются более удобные алгоритмы перевода, не требующие выполнения арифметических операций в различных системах счисления.
Каждая из приведенных в примерах систем счисления (десятичная, двоичная, восьмеричная и шестнадцатеричная) применяется в различных процессах, связанных с обработкой информации с помощью компьютера. Так, двоичная используется для организации машинных операций и хранения данных, восьмеричная и шестнадцатеричная – для представления машинных команд и адресов, десятичная же система остается удобной для ввода данных и представления результатов вычислений.
Длинные неструктурированные последовательности нулей и единиц двоичных чисел очень неудобны для зрительного восприятия человеком, который привык к гораздо более коротким и структурированным (десятки, сотни, тысячи и т.д.) последовательностям цифр, характерным для записи десятичных чисел. Для удобства восприятия таких чисел их переводят в систему счисления с основанием 8 или 16, являющимися степенями числа 2 и наиболее близкими к числу 10 (23 <10<24) с помощью очень простой процедуры. Она заключается в том, что двоичную последовательность разбивают справа налево на группы из трех цифр – триад или четырех цифр – тетрад, добавляя при необходимости незначащие нули. Затем каждая триада или тетрада заменяется соответствующей ей восьмеричной или шестнадцатеричной цифрой в соответствии с табл. 2.9.
Таблица 2.9
| Десятичное число | Восьмеричное число | Триадная форма записи двоичного числа | Шестнадца-теричное число | Тетрадная форма записи двоичного числа |
| 000 000 | ||||
| 000 001 | ||||
| 000 010 | ||||
| 000 011 | ||||
| 000 100 | ||||
| 000 101 | ||||
| 000 110 | ||||
| 000 111 | ||||
| 001 000 | ||||
| 001 001 | ||||
| 001 010 | А | |||
| 001 011 | В | |||
| 001 100 | С | |||
| 001 101 | D | |||
| 001 110 | Е | |||
| 001 111 | F |
Следующий пример показывает, как легко можно переводить двоичные числа в восьмеричные или шестнадцатеричные и наоборот с использованием описанного выше способа:
11010100  =
= 

 = 324
= 324  =
= 
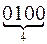 = D4
= D4 
Арифметические операции во всех позиционных системах счисления выполняются так же, как в десятичной системе счисления. ПС этому сложение двух чисел, например, в двоичной системе можно выполнять столбиком, начиная с младшего разряда и учитывая перенос единицы в старший разряд, например: