Лекция 2. Ранг матрицы. Системы линейных алгебраических уравнений
Пространство арифметических векторов
Определение 1.1 Всякая упорядоченнаясовокупность n действительных чисел называется действительным арифметическим вектором и обозначается
x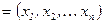 
,
Числа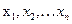 
называются компонентами арифметического вектора x.
Линейные операции над арифметическими векторами:
1) Если x 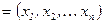и y 
, то x+y 
;
2) Если x 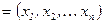арифметический вектор и 
R, то l x 
.
Определение 1.2 Множество всех действительных n -компонентных арифметических векторов с введенными выше операциями сложения и умножения на число называется пространством арифметических векторов, обозначаемое символом Rn.
Определение 1.3 Система арифметических векторов { x1, x2,…,xn }называется линейно зависимой, если найдутся числа l1, l2,…,ln , не равные одновременно нулю, такие, что l1 x1 + l2 x2 +…+ln xn= 0, где 0 = (0, 0, …,0) – нулевой вектор. В противном случае эта система называется линейно независимой.
Пусть Q – произвольное множество арифметических векторов.
Определение 1.4.4 Система векторов B = (е1, е2,…,еs) называется базисом в Q, если выполняются следующие условия:
1) ekÎQ, k = 1,2,…, s;
2) система B = {е1, е2,…,еs} линейно независима;
3) для любого вектора х ÎQ найдутся числа l1, l2,…,ln , такие, что х = 
e k (1.1)
Формула (1) называется разложением вектора х по базису B. Коэффициентыl1, l2,…,ls называются координатами этого вектора в базисе B.
Справедливы следующие утверждения:
1) всякая система векторов QÎ Rn имеет, по меньшей мере, один базис;
2) все базисы этой системы состоят из одинакового числа векторов, называемого рангом системы Q, обозначаемого 
или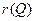 
;
3) ранг всего пространства Rn равен n и называется размерностью этого пространства, при этом в качестве базиса Rn можно взять следующую систему:
e1 =(1, 0, 0,…,0),
e2 =(0, 1, 0,…,0),
e3 =(0, 0, 1,…,0),
………………..
en =(0, 0, 0,…,1),
Этот базис называется каноническим.
Если система векторов n-мерного пространства содержит более чем n векторов, то она обязательно будет линейно зависимой.
Базисом n-мерного пространства Rn называется совокупность n линейно независимых векторов этого пространства.
Зафиксируем произвольный базис B = {е1, е2,…,еn} в пространствеRn. Тогда всякому вектору х можно поставить во взаимно однозначное соответствие столбец его координат в этом базисе, т.е.
x = x1 e1 + x2 e2 +….+ xn en или 
Замечание. Координаты вектора совпадают с его компонентами только в каноническом базисе.
Линейные операции над арифметическими векторами в координатной форме имеют вид:
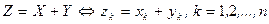
Ранг матрицы
Рассмотрим матрицу А размера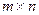 
. Выберем в этой матрице произвольно k строк и k столбцов 
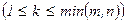. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называют минорами k-ого порядка матрицы А.
Например, из матрицы 
можно составить 12 миноров 1-ого порядка – это сами элементы матрицы А. Если выбрать какие-либо две строки и два столбца матрицы, то получим миноры 2-ого порядка, например 
. Минорами 3-его порядка являются определители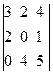 
=0,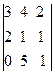 
=0, 
=0, 
=0. Все определители 3-его порядка равны «0», среди миноров 2-ого порядка есть неравные «0».
Если у матрицы все миноры порядка 
равны «0», а среди миноров порядка n имеется хотя бы один, отличный от «0», то число r называется рангом матрицы и обозначается 
Определение 2.1 Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.
Определение 2.2 Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Определение 2.3 Столбцы (строки) матрицы, входящие в матрицу базисного минора, называются базисными.
Теорема 2.1 (о базисном миноре). Всякий столбец ( строка ) матрицы есть линейная комбинация базисных столбцов ( строк ) этой матрицы.
Отметим свойства ранга матрицы:
1) при транспонировании матрицы ее ранг не меняется;
2) если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится;
3) ранг матрицы не изменится при элементарных преобразованиях матрицы.
Приведем основные методы вычисления ранга матрицы.
Метод окаймляющих миноров. Пусть в матрице найден минор k -го порядка М, отличный от нуля. Рассмотрим лишь те миноры (k +1)-го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. Если среди окаймляющих миноров найдется ненулевой минор (k +1)-го порядка, то вся процедура повторяется.
Пример 2.1. Найти ранг матрицы
Фиксируем минор 2-го порядка, отличный от нуля; 
.
Минор 3=го порядка, окаймляющий минор M2 ,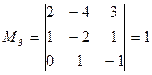 
также отличен от нуля. Однако оба минора четвертого порядка, окаймляющих минор M3, равны нулю:
, 
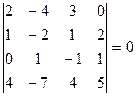. Следовательно, 
Вычисление ранга матрицы перебором всех её миноров очень трудоёмко. Простейший способ определения ранга матрицы состоит в приведении ее к ступенчатому виду при помощи последовательности элементарных преобразований, когда все элементы, расположенных ниже главной диагонали равны «0». К э лементарным преобразованиям матрицы относятся следующие операции:
1) умножение всех элементов некоторой строки матрицы на число 
;
2) перемена местами строк матрицы;
3) прибавление к какой-либо строке линейной комбинации других строк.
Если матрица В получена из матрицы А элементарными преобразованиями, то матрицы А и В называются эквивалентными 
. Ранг исходной матрицы будет равен числу ненулевых строк преобразованной матрицы.
Например,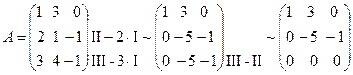 
, следовательно, 
Теорема 2.2 (о ранге матрицы) Максимальное число линейно независимых столбцов матрицы равно максимальному числу линейно независимых строк и равно рангу этой матрицы.
Доказательство.
Если ранг матрицы нулевой, то все ее элементы нулевые и среди них нет линейно независимых.
Пусть ранг матрицы равен r >0. Рассмотрим матрицу, составленную из r базисных столбцов матрицы. Она имеет ненулевой минор r -го порядка и, следовательно, ее столбцы линейно независимы.
Выберем k > r столбцов матрицы и покажем, что эти столбцы линейно зависимы. Построим из выбранных столбцов матрицу A *. Ее ранг 
, поскольку A * является частью матрицы A. Следовательно, 
и в матрице A * есть, по крайней мере, один небазисный столбец, и тогда столбцы матрицы A линейно зависимы.
Системы линейных алгебраических уравнений и их исследование
Определители и матрицы широко применяются при решении систем линейных уравнений. В наиболее общем виде такие системы записываются в форме
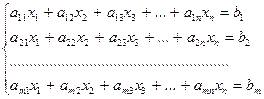(3.1)
Числа 
называются коэффициентами системы или коэффициентами при неизвестных. Числа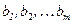 
называются свободными членами. Если все свободные члены равны нулю, то система называется однородной, если же, хотя бы одно из них отлично от нуля, то неоднородной.
Определение 3.1 Упорядоченный наборчисел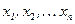 
называется частным решением системы(3.1), если при подстановке этих чисел в систему мы получаем верные равенства.
Частное решение системы линейных уравнений также может быть записано в виде столбца .
Совокупность всех частных решений системы линейных уравнений (3.1) назовем общим решением системы (3.1).
Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения - неопределенной, не имеющая ни одного решения - несовместной. Решить систему(3.1) - это значит указать все множество ее решений или доказать ее несовместность.
Определение 3.2 Две системы линейных уравнений называются равносильными, если каждое решение второй системы является решением первой и наоборот.
Если над системой (3.1) выполнить преобразования, а именно: поменять местами уравнения; умножить обе части любого уравнения системы на любое не равное нулю число; прибавить к обеим частям одного из уравнений системы соответствующие части другого уравнения, умноженные на любое действительное число, то система (3.1) переходит в равносильную ей систему. Перечисленные выше преобразования называются элементарными преобразованиями системы. В результате элементарных преобразований может случиться, что в системе появится уравнение, все коэффициенты которого равны нулю. Тогда, если и свободный член этого уравнения равен нулю, то уравнение справедливо при любых 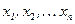и, следовательно, его можно отбросить. Если же свободный член не равен нулю, то этому уравнению не удовлетворяют никакие значения неизвестных, следовательно, полученная система является несовместной, а это означает, что несовместна и исходная система.
Определение 3.3 Матрица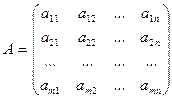 
называется основной матрицей системы (3.1), а матрица 
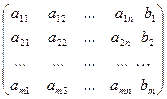– расширенной матрицей этой системы.