Совершенными (плотно упакованными) называют коды, в которых выполняются соотношения 
, где D - максимальная кратность исправляемых ошибок; b - основание кода; r - число проверочных символов.
Они отличаются тем, что позволяют исправлять все ошибки кратностью D или меньше и ни одной ошибки кратности больше D.
Число известных совершенных кодов ограничено кодами Хэмминга значности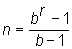 
и бинарным циклическим кодом Голея.
Квазисовершенными принято называть коды, исправляющие все ошибки кратности D и 
ошибок кратности D +1 при условии, что 
.
Класс квазисовершенных кодов значительно шире, чем класс плотно упакованных кодов.
Совершенные и квазисовершенные коды обеспечивают максимум вероятности правильного приема комбинации при равновероятных ошибках в канале связи.
Циклические коды
Был предложен ряд кодов и способов декодирования, при которых сложность декодера растет не экспоненциально, а лишь как некоторая степень n. В классе линейных систематических двоичных кодов это - циклические коды. Циклические коды просты в реализации и при невысокой избыточности обладают хорошими свойствами обнаружения ошибок. Циклические коды получили очень широкое распространение как в технике связи, так и в компьютерных средствах хранения информации. В зарубежных источниках циклические коды обычно называют избыточной циклической проверкой (CRC, Cyclic Redundancy Check).
Рассмотрим данный класс кодов подробнее. Название циклических кодов связано с тем, что каждая кодовая комбинация, получаемая путем циклической перестановки символов, также принадлежит коду. Так, например, циклические перестановки комбинации 1000101 будут также кодовыми комбинациями 0001011, 0010110, 0101100 и т.д.
Представление кодовых комбинаций в виде многочленов F(x) позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2. Деление осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложения по модулю 2. Циклическая перестановка кодовой комбинации эквивалентна умножению полинома F(x) на x с заменой на единицу переменной со степенью, превышающую степень полинома.
Любой полином G(x) степени r<n, который делит без остатка двучлен xn- 1, может быть порождающим полиномом циклического (n,k)-кода, где k = n - r. В этот код входят те полиномы, которые без остатка делятся на G(x).
Особую роль в теории циклических кодов играют неприводимые многочлены G(x), т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней.
Идея построения циклического кода (n,k) сводится к тому, что полином Q(x), представляющий информационную часть кодовой комбинации, нужно преобразовать в полином F(x) степени не более n -1, который без остатка делится на порождающий полином G(x) (неприводимый многочлен) степени r = n - k. Рассмотрим последовательность операций построения циклического кода.
· Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x).
· Умножаем Q(x) на одночлен xrи получаем Q(x)xr.
· Делим полином Q(x)xrна порождающий полином G(x) степени r, при этом получаем частное от деления C(x) такой же степени, что и Q(x).
где R(x) - остаток от деления Q(x)xrна G(x).
Умножив обе части на G(x), получим 
.
Полином F(x) делится без остатка на G(x), т.е. представляет собой разрешенную комбинацию циклического (n,k)-кода.
Таким образом, разрешенную кодовую комбинацию циклического кода можно получить двумя способами: умножением кодовой комбинации простого кода C(x) на полином G(x) или умножением кодовой комбинации Q(x) простого кода на одночлен xrи добавлением к этому произведению остатка R(x).
В первом случае информационные и проверочные разряды не отделены друг от друга (код получается неразделимым). Во втором случае получается разделимый код. Этот код достаточно широко используется на практике, поскольку процесс декодирования и обнаружения ошибок при использовании разделимого кода выполняется проще.
Рассмотрим пример разделяемого циклического кода (9,5) с порождающим полиномом 
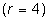. В качестве информационной части кодовой комбинации возьмем полином 
.
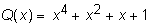Умножение Q(x) на xrэквивалентно повышению степени многочлена на r. Q(x) = 
® 10111.
Q(x)xr = 
® 101110000
Формирование проверочной группы осуществляется в процессе деления Q(x)xr на G(x).
В результате деления получаем частное от деления C(x) = x4+x2® 10100 и остаток от деления R(x) = x3+x2® 1100. Для получения разрешенной кодовой комбинации остаток (проверочная группа) помещается на место "пустых" разрядов Q(x)xr, т.е. F(x)= 
® 101111100. Данная комбинация отправляется в канал связи. Аналогичные операции выполняются для других информационных комбинаций.
Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок.
При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.
Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью и будут рассмотрены ниже в подразделе 6.1.2.8.
Прочие классы кодов
Наряду с циклическими кодами на практике используются другие типы кодов, обладающие различными свойствами. Подробное рассмотрение классов кодов выходит за рамки настоящего курса, поэтому приведем только их краткую характеристику.
Среди циклических кодов особое значение имеет класс кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза - Чоудхури - Хоквингема (обозначаемые сокращением БЧХ) отличаются сравнительно просто реализуемой процедурой декодирования.
Относительно простой является процедура мажоритарного декодирования, применимая для некоторого класса двоичных линейных, в том числе циклических кодов. Основана она на том, что в этих кодах каждый информационный символ можно несколькими способами выразить через другие символы кодовой комбинации.
Мощные коды (т.е. коды с длинными блоками и большим кодовым расстоянием d) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код из двух линейных систематических кодов (n1,k1) и (n2,k2). Минимальное кодовое расстояние для двумерного итеративного кода d=d1d2, где d1 и d2 - соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступеней.
На итеративный код похож каскадный код, но между ними имеется существенное различие. Первая ступень кодирования в каскадном коде является линейным систематическим двоичным кодом (внутренний код), каждая комбинация которого рассматривается как один символ недвоичного кода второй ступени (внешнего). При приеме сначала декодируются (с обнаружением или исправлением ошибок) все строки (блоки) внутреннего кода, а затем декодируется блок внешнего m-ичного кода, причем исправляются ошибки и стирания, оставшиеся после декодирования внутреннего кода. В качестве внешнего кода используют обычно m-ичный код Рида-Соломона, который является подклассом кодов БЧХ и обеспечивает наибольшее возможное d при заданных n2 и k2, если n2<m. Каскадные коды во многих случаях наиболее перспективны среди известных блочных помехоустойчивых кодов.
Метод перемежения
Для каналов с группированием ошибок часто применяют метод перемежения символов, или декорреляции ошибок. Он заключается в том, что символы, входящие в одну кодовую комбинацию, передаются не непосредственно друг за другом, а перемежаются символами других кодовых комбинаций.
Если интервал между символами, входящими в одну комбинацию, сделать больше максимально возможной длины группы ошибок, то в пределах комбинации группирования ошибок не будет. Группа ошибок распределится в виде одиночных ошибок на группу комбинаций. Одиночные ошибки будут легко обнаружены (исправлены) декодером.