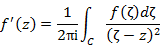Краткая история
Огюстен-Луи Коши – французский математик начала 19 века. Родился в 1789 году в семье высокопоставленного офицера парижской полиции. Через месяц после его рождения случилась Революция, но его семья её успешно пережила и смогла дать ему образование сначала в одной из лучших парижских школ, а затем и в Политической школе, одном из лучших и по сей день учебном заведении Франции.
Он внёс огромный вклад во много областей математики, в частности в математический анализ и математическую физику. То, что сегодня называется «интегральной формулой Коши», было представлено им в письмах Туринской академии наук в 1831, где он оказался по случаю очередных волнений во Франции (революции 1830 года).
Вывод интегральной формулы Коши
Выведем интегральную формулу Коши. Для этого введём некоторые обозначения.
Пусть функция 
является аналитической в односвязной области J, ограниченной контуром C. Возьмём произвольную внутреннюю точку 
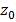и построим замкнутый контур Γ, целиком лежащий в J и содержащий точку 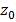внутри себя. Рассмотрим вспомогательную функцию 
.
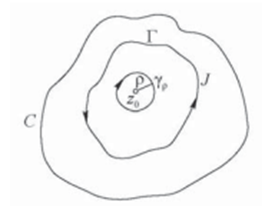
Функция 
является аналитической функцией всюду в области J, за исключением точки 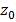. Поэтому если мы в области J возьмём такой замкнутый контур γ, лежащий внутри Γ, чтобы точка 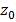попала внутрь области, ограниченной контуром γ, то функция будет аналитической в двусвязной области J’, заключённой между контурами Γ и γ. Согласно теореме Коши, интеграл от функции по кривой Γ+ γ равен нулю: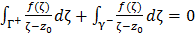 
. Изменив направление интегрирования во втором интервале, перепишем это равенство в виде 
. Стоящий слева интеграл не зависит от выбора контура γ, следовательно этим свойством обладает и интеграл, стоящий справа. Для дальнейшего рассмотрения удобно в качестве контура интегрирования γ выбрать окружность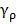 
некоторого радиуса 
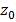c центром в точке . Положив 
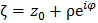, имеем 
. Преобразуем последний интеграл:
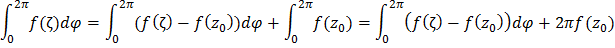
Теперь пусть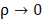 
. Так как функция – аналитическая, а следовательно, непрерывная в области J, то для любого положительного числа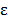 
можно указать такое значение , что 
для 
. Отсюда следует, что при 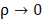существует предел 
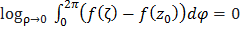. Так как в формуле 
последнее слагаемое не зависит от , то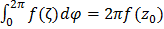 
, а следовательно 
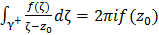; Согласно 
получим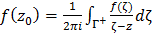 
.
Интеграл, стоящий в правой части, выражает значение аналитической функции f(z) в некоторой точке 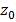через её значения на любом контуре Γ, лежащем в области аналитичности функции f(z) и содержащем точку 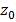внутри. Этот интеграл и называется интегралом Коши.
Вообще, 
– не единственный способ записи интегральной формулы. Также её можно записать в ви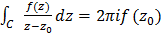де: 
, где 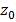- точка, находящаяся в контуре C.
Следствия из формулы Коши
Рассмотрим два следствия формулы Коши.
1. Интеграл вида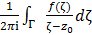 
по замкнутому контуру Γ, целиком лежащему в области J аналитичности функции f(z), имеет смысл для любого положения точки 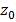на комплексе плоскости при условии, что эта точка не лежит на контуре Γ. При этом, если точка 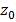лежит внутри Γ, значение интеграла равно 
, если вне Γ – нулю, поскольку в этом случае подынтегральная функция аналитическая внутри всюду Γ. Итак, 
2. Пусть f(z) – аналитическая функция в односвязной области J и 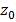– некоторая внутренняя точка этой области. Опишем из этой точки окружность радиуса 
, целиком лежащую в области J. Тогда по формуле Коши 
. Но на окружности 
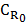выполняется 
, поэтому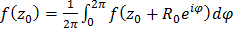 
, или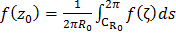 
. Эта формула носит название формулы среднего значения и выражает значение аналитической функции в центре окружности как среднее из её граничных значений.
Примеры решения задач
Итак, рассмотрим несколько задач различной степени сложности на интегральную формулу Коши. При решении задач обычно используют графическое представление в виде рисунка комплексной плоскости, где изображают сам контур и .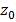
1. 
.
Воспользуемся «альтернативной» формой записи формулы Коши: 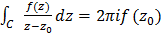. Тогда 
, 
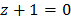, и из формулы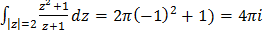 
.
2. 
.
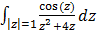Поступим аналогично, но выделим из знаменателя z: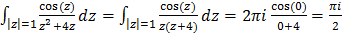 
3. 
.
Здесь важно обратить внимание, что 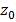будет комплексным числом: 
4. 
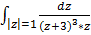
Очевидно,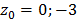 
, тогда: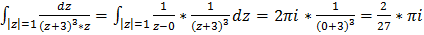 
Интегралы типа Коши
В теории функций важную роль играет также так называемый интеграл типа Коши, частным случаем которого и будет сам интеграл Коши. Выглядит он следующим образом:
От интеграла Коши он отличается тем, что контур 
здесь не обязательно замкнутый, а функция только непрерывна и не обязана быть аналитической на . Интеграл типа Коши определяет однозначную функцию F(z) во всякой области G, не содержащей ни одной точки кривой . Эта функция обладает производными любого порядка (то есть её можно дифференцировать бесконечно) в области G, причём её производная любого порядка n может быть получена путём n-кратного дифференцирования по z подынтегральной функции:
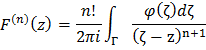
Из этой теоремы следуют важные следствия. Их, как и теорему, мы доказывать не будем, т.к. это несколько выходит за тему реферата.
1. Каждая функция комплексного переменного, аналитическая в некоторой области G, бесконечно дифференцируема в этой области.
2. Произвольные любого порядка от функции f(z), аналитической в области G, также являются аналитическими в этой области
3. Каждая функция f(z), однозначная и непрерывная в некоторой односвязной области G и такая, что интеграл от f(z), взятый по любому треугольному контуру Δ, лежащему в области, равен нулю, является аналитической в этой области (теорема Морера)
Следствия из формулы
Формула Коши – одна из важнейших в ТФКП, и у неё есть множество важных следствий.
1. Принцип максимума аналитической функции. Пусть функция f(z) является аналитической в области J и непрерывной в замкнутой области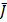 
. Тогда или 
, или максимальные значения достигаются только на границе области.
2. Использую формулу Коши, можно доказать, что производная аналитической функции также является аналитической функцией, то есть:
