Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Новгородский государственный университет имени Ярослава Мудрого»
Институт электронных и электронных систем
________________________________________________________
Кафедра алгебры и геометрии
МАТЕМАТИКА
Методические указания по изучению дисциплины
И контрольные задания
Направление подготовки 09.03.01 – Информатика и вычислительная техника
Профиль – Программное обеспечение вычислительной техники и автоматизированных систем
Форма обучения: заочная
Семестр
Великий Новгород
ВВЕДЕНИЕ
Курс математики играет важную роль в подготовке специалистов. Количественные методы анализа необходимы всем специальностям. Математика является фундаментальной дисциплиной. Ее преподавание предусматривает:
- развитие логического и алгоритмического мышления;
- овладение основными методами исследования и решения математических задач;
- выработку умения самостоятельно расширять математические знания и проводить
математический анализ прикладных задач.
Общие указания к выполнению контрольной работы
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих этапов:
- Изучение нужного материала по учебнику (смотрите список литературы). При этом необходимо усвоить основные определения, понятия, формулировки теорем, вывод необходимых формул.
- Чтение учебника должно сопровождаться решением задач, решение задач следует излагать подробно, вычисления располагать в строгом порядке, каждый шаг решения объяснять, почему применяли именно эту формулу.
- После изучения определенной темы и решения достаточного количества задач рекомендуется по памяти воспроизвести определения, выводы формул, формулировки и доказательства теорем, ответить на вопросы для самопроверки и только тогда приступить к выполнению контрольной работы.
Контрольную работу удобнее всего выполнять в ученической тетради. На обложке должны быть указаны: фамилия студента, его инициалы, домашний адрес и дата отправления работы в университет, номер варианта.
Каждый студент выполняет тот вариант контрольной работы, номер которого совпадает с последней цифрой номера его зачетной книжки (из каждого задания нужно взять пример под соответствующим номером).
Решение задач контрольной работы нужно располагать в порядке номеров, указанных в работе. Перед решением задачи следует записать ее условие. Работа должна быть аккуратно оформлена, разборчиво написана, содержать ссылки на соответствующие формулы или теоремы по поводу произведенных вычислений. Не следует пропускать промежуточные действия, не допускается сокращение слов.
Выполненная контрольная работа присылается в университет не позднее, чем за три недели до начала очередной сессии.
Во время сессии назначается время для собеседования по работе. Если студент сумел правильно объяснить, как он решил ту или иную задачу, почему применял именно эту формулу, работа считается зачтенной.
Методические указания по дисциплине составила доцент кафедры алгебры и геометрии О.П. Матвеева.
Таблица выполнения контрольных работ
| Направления подготовки | № контрольной работы | семестры |
| Информатика и вычислительная техника | к.р. №1 | I |
| к.р. №2 | II | |
| к.р. №3 | III |
Задание 1.
Решить дифференциальные уравнения.
1. а) 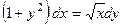 б)
б) 
в)  г)
г) 
2. а)  б)
б) 
в) 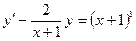 г)
г) 
3. а) 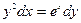 б)
б) 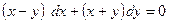
в) 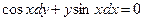 г)
г) 
4. а)  б)
б) 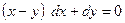
в)  г)
г) 
5. а) 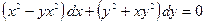 б)
б) 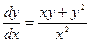
в) 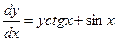 г)
г) 
6. а) 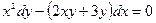 б)
б) 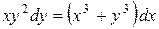
в) 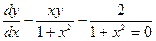 г)
г) 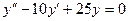
7. а)  б)
б) 
в)  г)
г) 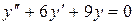
8. а) 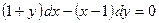 б)
б) 
в)  г)
г) 
9. а)  б)
б) 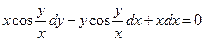
в)  г)
г) 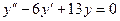
10. а)  б)
б) 
в) 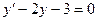 г)
г) 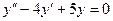
Задание 2.
Первые два ряда исследовать на сходимость, используя признак сравнения, Коши, Даламбера, последний ряд - на абсолютную или условную сходимость.
1. 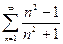


2. 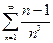
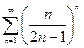

3. 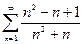
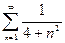

4. 


5. 
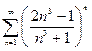

6. 


7. 


8. 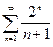
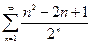

9. 
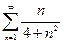

10. 
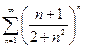

Задание 3.
Двойные интегралы. Изменить порядок интегрирования. Сделать чертёж области интегрирования.
1.  3.
3.  5.
5. 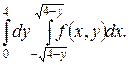 7.
7.  9.
9. 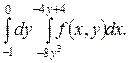
| 2.  4.
4.  6.
6.  8.
8.  10.
10. 
|
Задание 4.
Вычислить двойной интеграл  для функций
для функций 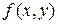 и областей D, перечисленных ниже.
и областей D, перечисленных ниже.
1. 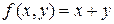 , D:
, D:  ;
;
2.  , D:
, D: 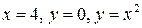 ;
;
3.  , D:
, D:  ;
;
4. 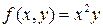 , D:
, D:  ;
;
5.  , D:
, D: 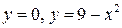 ;
;
6. 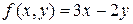 , D:
, D:  ;
;
7. 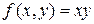 , D:
, D:  ;
;
8.  , D:
, D:  ;
;
9. 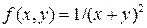 , D:
, D:  ;
;
10. 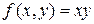 , D:
, D: 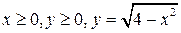 .
.
Задание 5.
Вычислить в полярных координатах двойной интеграл  для функций
для функций 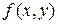 и областей D, перечисленных ниже.
и областей D, перечисленных ниже.
1.  , D:
, D: 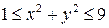 ;
;
2.  , D:
, D:  ;
;
3. 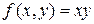 , D:
, D:  ;
;
4. 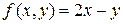 , D:
, D:  ;
;
5. 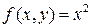 , D:
, D:  ;
;
6. 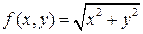 , D:
, D: 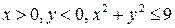 ;
;
7.  , D:
, D:  ;
;
8.  , D:
, D:  ;
;
9.  , D:
, D: 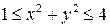 ;
;
10. 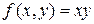 , D:
, D:  ;
;
Задание 6.
Функции многих переменных.
1. Дана функция 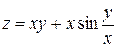 . Показать, что
. Показать, что  .
.
2.Дана функция  . Показать, что
. Показать, что  .
.
3. Дана функция 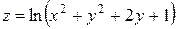 . Показать, что
. Показать, что 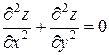 .
.
4. Дана функция 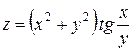 . Показать, что
. Показать, что 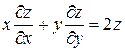 .
.
5. Дана функция  . Показать, что
. Показать, что 
6. Дана функция 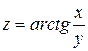 . Показать, что
. Показать, что 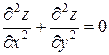 .
.
7. Дана функция  . Показать, что
. Показать, что  .
.
8. Дана функция  . Показать, что
. Показать, что 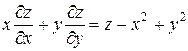 .
.
9. Дана функция 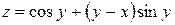 . Показать, что
. Показать, что  .
.
10. Дана функция 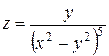 . Показать, что
. Показать, что 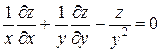 .
.
Задание 7.
1. Вычислите криволинейный интеграл по координатам дуги  вдоль параболы вдоль параболы 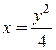 , ,  . .
|
2. Вычислите криволинейный интеграл по координатам дуги  по прямой по прямой  от от 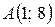 до до 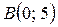 . .
|
3. Вычислите криволинейный интеграл по координатам дуги  , если путь от точки , если путь от точки 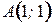 до точки до точки  - отрезок прямой. - отрезок прямой.
|
4. Вычислите криволинейный интеграл по длине дуги 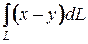 , где , где  - отрезок прямой от - отрезок прямой от  до до  . .
|
5. Вычислите криволинейный интеграл по координатам дуги  вдоль прямой вдоль прямой  , , 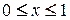 . .
|
6. Вычислите криволинейный интеграл по координатам дуги  по прямой по прямой  , , 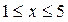 . .
|
7. Вычислите криволинейный интеграл по длине дуги 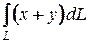 , где , где  - ломаная - ломаная  : :  , ,  , ,  . .
|
8. Вычислите криволинейный интеграл по длине дуги 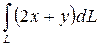 , где , где  : :  , , 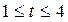 . .
|
9. Вычислите криволинейный интеграл по координатам дуги  вдоль параболы вдоль параболы  от точки от точки 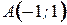 до точки до точки 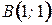 . .
|
10. Вычислите криволинейный интеграл по длине дуги 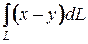 , где , где  - отрезок прямой от - отрезок прямой от 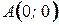 до до 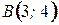 . .
|
Задание 8.
Математическая логика. Применяя равносильные преобразования, приведите следующие формулы к возможно более простой форме:
1) 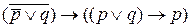 ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10) 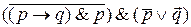 .
.
Задание 9.
Упростить РКС.
1.

2.

3.

4.

5.

6.

7.

8.

9.
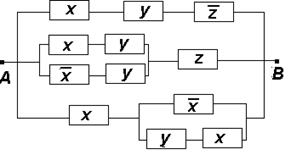
10.

Примеры решения заданий
Решить дифференциальные уравнения.
1)  .
.
Решение. Преобразуем данное уравнение, вынося общий множитель 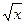 и заменяя
и заменяя  на
на 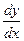 . Имеем
. Имеем  . Это уравнение с разделяющимися переменными. Разделим обе части уравнения на
. Это уравнение с разделяющимися переменными. Разделим обе части уравнения на  .
.
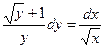 .
.
Интегрируя, имеем:
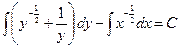 .
.

Последнее равенство дает общее решение данного уравнения в неявном виде.
2)  .
.
Решение. Данное уравнение есть линейное уравнение первого порядка. Будем искать его решение в виде произведения двух функций  и
и  , а именно в виде:
, а именно в виде:
 , тогда
, тогда  .
.
Подставим эти выражения для  и
и  в данное уравнение:
в данное уравнение:

Сгруппируем слагаемые в левой части
 (1)
(1)
Пусть функция  такова, что она является решением уравнения
такова, что она является решением уравнения 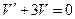 . Это уравнение с разделяющими переменными. Найдем из него функцию
. Это уравнение с разделяющими переменными. Найдем из него функцию  .
.
 .
.
Постоянную  здесь полагаем равную нулю.
здесь полагаем равную нулю.
Подставим найденное значение  в (1). Получим еще одно уравнение с разделяющимися переменными:
в (1). Получим еще одно уравнение с разделяющимися переменными:  или
или  . Интегрируя имеем:
. Интегрируя имеем:  , т.е.
, т.е.  . Тогда
. Тогда  .
.
Это и есть общее решение уравнения.
3) а) 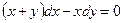
Данное уравнение является однородным уравнением первой степени относительно переменных  и
и  , т.к. оно имеет вид:
, т.к. оно имеет вид: 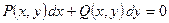 и функции
и функции  ,
,  являются однородными функциями первого порядка. Действительно:
являются однородными функциями первого порядка. Действительно: 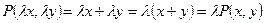 .
.  .
.
Такое уравнение при помощи подстановки 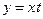 или
или  приводится к уравнению с разделяющимися переменными. Действительно, полагая
приводится к уравнению с разделяющимися переменными. Действительно, полагая  , где
, где 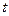 - новая функция от
- новая функция от  , найдем
, найдем  . Подставим в данное уравнение, получим
. Подставим в данное уравнение, получим
 . После упрощения имеем:
. После упрощения имеем:

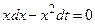 или
или  .
.
Таким образом, получим уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, находим:
 .
.
Это и есть общее решение данного уравнения.
б) Однородное уравнение может быть записано в виде:  . Выполняя ту же подстановку
. Выполняя ту же подстановку 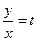 , придем к уравнению с разделяющимися переменными. Например.
, придем к уравнению с разделяющимися переменными. Например.  . Разделим на
. Разделим на  . Имеем (1)
. Имеем (1)  . Заменяя
. Заменяя 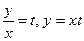 . Отсюда
. Отсюда  подставим в уравнение (1).
подставим в уравнение (1).
 или
или  . Решая его как уравнение с разделяющимися переменными, имеем:
. Решая его как уравнение с разделяющимися переменными, имеем:

Разделим на  , получим:
, получим:
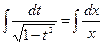 или
или 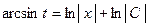 ,
,  ,
,  .
.
И окончательно общее решение уравнения имеет вид:
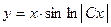
4) Уравнение вида: (1) 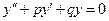 , где
, где 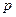 и
и 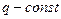
называется однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для отыскания общего решения такого уравнения составляется характеристическое уравнение  (2), которое получается заменой
(2), которое получается заменой  и
и  на соответствующие степени
на соответствующие степени 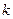 , причем сама функция
, причем сама функция  записывается единицей.
записывается единицей.
Общее решение уравнения (1) записывается в зависимости от корней уравнения (2).
Здесь возможны случаи:
| № | Корни характеристического уравнения | Вид общего решения уравнения (1) |
 и и  -действительные и различные корни уравнения (2) -действительные и различные корни уравнения (2)
| 
| |
 и и  -действительные и равные корни уравнения (2) -действительные и равные корни уравнения (2) 
| 
| |
 и и  -комплексные корни уравнения (2) -комплексные корни уравнения (2) 
| 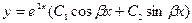
|
Например:
1) 
 .
.
2) 
При исследовании числовых рядов с положительными членами на сходимость, необходимо знать, что если ряд  - сходится, то
- сходится, то 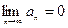 . Если же
. Если же  , то ряд расходится. Для исследования ряда на сходимость чаще всего применяют один из следующих достаточных признаков.
, то ряд расходится. Для исследования ряда на сходимость чаще всего применяют один из следующих достаточных признаков.
Признак Даламбера (практическое правило).
Находим 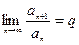 . Если
. Если 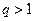 , то ряд расходится, если
, то ряд расходится, если  , то ряд сходится, если
, то ряд сходится, если  , то нужно применить другой достаточный признак.
, то нужно применить другой достаточный признак.
Например:
а)  .
.
Тогда  .
.
Значит ряд расходится.
б)  .
.
Тогда  .
.
И ряд расходится.
в) 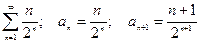 .
.
Тогда 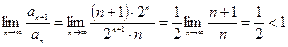 .
.
Ряд сходится.
Признак сравнения.
Если  , начиная с некоторого
, начиная с некоторого  и ряд
и ряд  сходится, то сходится и ряд
сходится, то сходится и ряд  Если же ряд (2) расходится, то расходится и ряд (1). При этом полезно помнить, что ряды:
Если же ряд (2) расходится, то расходится и ряд (1). При этом полезно помнить, что ряды:
1)  расходится (гармонический ряд);
расходится (гармонический ряд);
2) 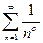 расходится, если
расходится, если  и сходится, если
и сходится, если  (обобщенный гармонический ряд);
(обобщенный гармонический ряд);
3)  (геометрическая прогрессия). При
(геометрическая прогрессия). При  сходится, а при
сходится, а при  расходится.
расходится.
Например:
а) 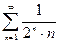 . Замечаем, что при
. Замечаем, что при  общий член исходного ряда
общий член исходного ряда 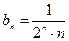 меньше общего члена ряда
меньше общего члена ряда  , т.е.
, т.е. 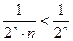 , но ряд
, но ряд  сходится, т.к.
сходится, т.к.  и это есть ряд геометрической прогрессии, тогда согласно признаку сравнения, сходится и исходный ряд
и это есть ряд геометрической прогрессии, тогда согласно признаку сравнения, сходится и исходный ряд 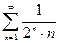 .
.
б)  ; общий член этого ряда
; общий член этого ряда  больше общего члена ряда
больше общего члена ряда  А ряд
А ряд  расходится как гармонический ряд, все члены которого умножаются на 4. Значит исходный ряд тоже расходится.
расходится как гармонический ряд, все члены которого умножаются на 4. Значит исходный ряд тоже расходится.
в)  . Общий член этого ряда
. Общий член этого ряда  (1)
(1)
Ряд  сходится как обобщенный гармонический ряд, т.к.
сходится как обобщенный гармонический ряд, т.к.  . Тогда исходный ряд сходится по признаку сравнения согласно неравенству (1).
. Тогда исходный ряд сходится по признаку сравнения согласно неравенству (1).