Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
22)
23) МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M (X) = x 1 p 1+ x 2 p 2+...+ xn pn.
Реально на основе данных выборки мы не можем вычислить M (X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M (X) ≈ `X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной: M (C) = C.
2. Постоянный множитель можно выносить за знак математического ожидания: M (CX) = CM (X).
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M (X + Y + Z) = M (X)+ M (Y)+ M (Z).
4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M (X × Y × Z) = M (X)× M (Y)× M (Z). Все эти свойства имеют большое практическое значение.
24) Свойства мат.ожидания. Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
25) ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D (X) = M (X - M (X)) 2. Для вычислений удобнее пользоваться формулой:
D (X) = M (X 2) - (M (X)) 2.
Дисперсия обладает следующими свойствами.
1. Дисперсия постоянной величины С равна нулю: D (C) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D (CX) = C 2 D (X).
3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:
D (X + Y + Z) = D (X)+ D (Y)+ D (Z).
4. Дисперсия суммы постоянной величины и случайной - равна дисперсии случайной величины: D (C + X) = D (X).
26) 1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n - частота (повторяемость фактора Х)
27) 1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.
28) Среднее квадратич.отклонение случ.величины
Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
29) Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
,
где 
— биномиальные коэффициенты, 
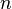— неотрицательное целое число.
30) Биномиальное распределение — дискретное распределение вероятностей случайной величины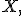 
принимающей целочисленные значения 
с вероятностями:
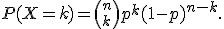
Данное распределение характеризуется двумя параметрами: целым числом 
называемым числом испытаний, и вещественным числом 
называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из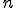 
независимых испытаний, в каждом из которых может произойти "успех" с вероятностью то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы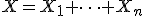 
независимых слагаемых, имеющихраспределение Бернулли.
31)
32) Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
· Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть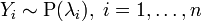 
. Тогда
.
· Пусть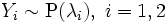 
, и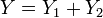 
. Тогда условное распределение 
при условии, что 
, биномиально. Более точно:
.
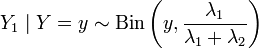33) Функцией распределения случайной величины Х называется функция F(х)выражающая для каждого хвероятность того что случайная величина Х примет значение меньше х
F(x) = P(X < x).
Функция F(х) называется также интегральной функцией распределения или интегральным законом распределения.
1Функция распределения случ.вел-.есть неотрицательная фунцкия заключенная между 0 и 1. 0меньшеили равно 6 F(x)меньшеилиравно1.
2Функция распред.случ.вел.- неубывающая функция на всей числовой оси
35)
1Функция распределения случ.вел-.есть неотрицательная фунцкия заключенная между 0 и 1
0 мееньшеилиравно F(x)меньшеилиравно 1.
2Функция распред.случ.вел.- неубывающая функция на всей числовой оси
3 на минус бесконечности функция распр. Равна 0.На плюс бесконечности 1
F(−1) = limx!−1F(x) = 0, F(1) = limx!+1F(x) = 1.
4Вереятность попадания случайной величины в интервал [х1,х2) включая х1 равна приращению ее функции распр.на интервале
P(x1 6 X < x2) = F(x2) − F(x1).
.37)Случайная величина Хназывается непрерывной если ее функция распределения непрерывна в любой точке и дефференциируема всюду кроме быть может отдельных точек
Вероятность любого отдельно взятого значения непрерывно случ.величины равна 0
38)Плотность вероятности или плотность распределения φ(x)непрерывной случайной величины х называется производная ее функции распределения
φ'(x) = F'(x)
матем.ожидание М(Х)=а= 
Дисперсия. D(Х)=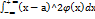 
39). Вероятность попадания случайной величины в заданный интервал
Может быть вычислена двумя способами:
1) через функцию распределения 
2) через плотность распределения 
40)
41) 1. Плотность распределения есть неотрицательная функция:
.
Это свойство непосредственно вытекает из того, что функция распределения 
есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
.
Это следует из формулы (5.4.4) и из того, что 
.
Геометрически основные свойства плотности распределения означают, что:
1) вся кривая распределения лежит не ниже оси абсцисс;
2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения , как всякая вероятность, есть величина безразмерная. Размерность плотности распределения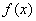 
, как видно из формулы (5.4.1), обратна размерности случайной величины.
· 42) Математическое ожидание числа есть само число.
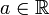— константа;
· Математическое ожидание линейно, то есть
,
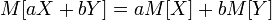где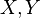 
— случайные величины с конечным математическим ожиданием, а 
— произвольные константы;
· Математическое ожидание сохраняет неравенства, то есть если 
почти наверное, и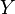 
— случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины 
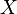также конечно, и более того
;
· Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если 
почти наверное, то
.
· Математическое ожидание произведения двух независимых случайных величин 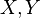равно произведению их математических ожиданий
.
Матем.ожидан и дисперсия непрерывн.случ.вел. Для описания определенных частных свойств непре рывной, случайной величины применяются такие же по смыслу числовые характеристики, как и для дискретных величин, но процедура определения их по заданным за конам распределения несколько иная. Различие состоит в том, что операции суммирования, применяемые в слу чае дискретных величин, должны быть заменены при непрерывных величинах интегрированием. В соответст вии с этим дадим определение тех же числовых характе ристик, что и ранее, применительно к непрерывным величинам.
Средним значением (математическим ожиданием) непрерывной, случайной величины называется неслу чайная величина, определяемая по формуле
|
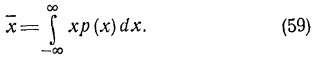
Формула соответствует выражению (31) для дискрет ных величин, но вероятность Р(х) здесь заменяется эле ментом вероятности р(х)dx,а сумма—интегралом.
|
Дисперсией называется величина, определяемая по формуле
Формула соответствует выражению (327) для ди скретных, случайных величин.
Корень квадратный из дисперсии s2 называется сред-неквадратическим отклонением.
Величина
|
представляет собой средний квадрат случайной вели чины.
|
Между дисперсией, средним квадратом и средним значением непрерывной, случайной величины существует такое же соотношение, как и в случае дискретных, слу чайных величин, а именно: