· 
Здесь u (t, x) — смещение струны из положения равновесия, или избыточное давление воздуха в трубе, или магнитуда электромагнитного поля в трубе, а c — скорость распространения волны. Для того, чтобы сформулировать задачу Коши в начальный момент времени, следует задать смещение и скорость струны в начальный момент времени:
Двумерное уравнение Лапласа
Уравнение Лапласа для неизвестной функции двух переменных имеет вид:
Его решения называются гармоническими функциями.
Связь с аналитическими функциями
Вещественная и мнимая части любой голоморфной функции 
комплексной переменной 
являются сопряжённо гармоническими функциями: они обе удовлетворяют уравнению Лапласа и их градиенты ортогональны. Если f = u + iv, то условия Коши-Римана утверждают следующее:
Складывая и вычитая уравнения друг из друга, получаем:
Также можно показать, что любая гармоническая функция является вещественной частью некоторой аналитической функции.
Граничные задачи
Граничные задачи ставятся следующим образом: найти функцию u, которая удовлетворяет уравнению Лапласа во всех внутренних точках области S, а на границе области 
— некоторому условию. В зависимости от вида условия различают следующие кравевые задачи:
— задача Дирихле
— задача Неймана
Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач (например проекционных методов, таких как метод Галёркина).
Решение разностной схемы называется приближенным решением дифференциальной задачи.
Хотя формальное определение не накладывает существенных ограничений на вид алгебраических уравнений, но на практике имеет смысл рассматривать только те схемы, которые каким-либо образом отвечают дифференциальной задаче. Важными понятиями теории разностных схем являются понятия сходимости, аппроксимации, устойчивости, консервативности
23 Задача численного дифференцирования. Аппроксимация производных.
Метод Рунге-Ромберга уточнения решения(https://neo-chaos.narod.ru/useful/nummethod/kalitkin_03_070-084.pdf)
Аппроксимация
Напомним, что производной функции y = f (x) называется предел отношения приращения функции D y к приращению аргумента D x при стремлении D x к нулю:
. (1)
Обычно для вычисления производных используют готовые формулы (таблицу производных) и к выражению (1) не прибегают. Однако в численных расчетах на ЭВМ использование этих формул не всегда удобно и возможно. В частности, функция y = f (x) может быть задана в виде таблицы значений. В таких случаях производную находят, опираясь на формулу (1). Значение шага D x полагают равным некоторому конечному числу и для вычисления значения производной получают приближенное равенство
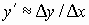. (2)
Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей (значения D y, D x в формуле (2) конечные в отличие от их бесконечно малых значений в (1)).
Рассмотрим аппроксимацию производной для функции y = f (x), заданной в табличном виде: y 0, y 1,… при x = x 0, x 1,…. Пусть шаг - разность между соседними значениями аргумента - постоянный и равен h. Запишем выражения для производной 
при x = x 1. В зависимости от способа вычисления конечных разностей получаем разные формулы для вычисления производной в одной и той же точке:
(3)
с помощью левых разностей;
(4)
с помощью правых разностей;
(5)
с помощью центральных разностей.
Можно найти также выражения для старших производных. Например,
. (6)
Таким образом, по формуле (2) можно найти приближенные значения производных любого порядка. Однако при этом остается открытым вопрос о точности полученных значений.