Определение кинетической энергии системы
Кинетическую энергию механизма находим как сумму кинетических энергий его звеньев
 .
.
Кинетическая энергия вращающегося маховика:
 ,
,
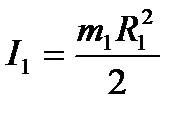 – момент инерции маховика относительно оси вращения.
– момент инерции маховика относительно оси вращения.
Кинетическая энергия поступательно движущейся кулисы:
 ,
,
Кинетическая энергия катка, совершающего плоское движение:
 ,
,
 – момент инерции катка относительно оси, проходящей через его центр масс.
– момент инерции катка относительно оси, проходящей через его центр масс.
Кинетическая энергия системы:
 .
.
После тождественных преобразований:
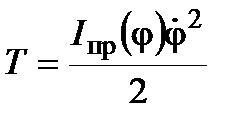 , (1)
, (1)
где  ,
,  .
.
– приведенный к ведущему звену момент инерции.
Определение производной кинетической энергии по времени
Производную кинетической энергии по времени находим по правилу вычисления производной произведения и производной сложной функции
 . (2)
. (2)
Здесь
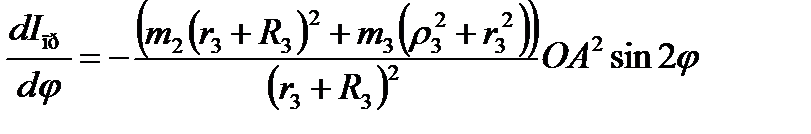 ,
,  .
.
2.3. Определение элементарной работы, мощности внешних сил. Определение работы внешних сил на конечном перемещении (механизм в горизонтальной плоскости).
В случае, когда механизм расположен в горизонтальной плоскости работу совершает только вращающий момент  . Элементарная работа при этом определяется равенством
. Элементарная работа при этом определяется равенством
 .
.
Мощность
 , (3)
, (3)
Работа при повороте маховика на угол 
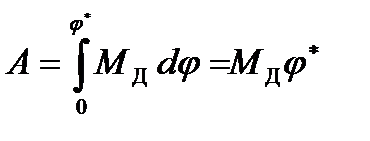 . (4)
. (4)
2.4. Определение угловой скорости маховика при его повороте на угол φ*
Для определения угловой скорости маховика применяем теорему об изменении кинетической энергии в конечной форме, полагая, что механизм в начальный момент находился в покое.
 ,
,  ,
,  .
.
Подстановка в это равенство найденных выражений (1) и (4) дает
 .
.
Тогда
 .
.
2.5. Определение углового ускорения маховика при его повороте на угол φ*
Воспользуемся теоремой об изменении кинетической энергией в дифференциальной форме
 ,
,  .
.
Подставляя в это уравнение найденные выше значения (2) и (3), находим
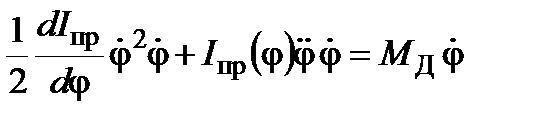 .
.
Откуда
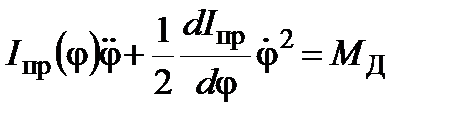
и

Дифференциальное уравнение второго порядка
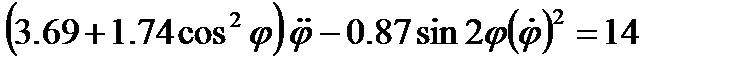 (5)
(5)
описывает движение кулисного механизма. Оно может быть проинтегрировано только численно, а также использовано для нахождения углового ускорения маховика в произвольном его положении.
Определим угловое ускорение маховика при угле его поворота  .
.
 .
.
Этап III. Реакции связей и уравновешивающая сила.
3.1. Определение реакций внешних и внутренних связей в положении φ*
Определим реакцию подшипника на оси маховика и силу, приводящую в движение кулису с помощью принципа д`Аламбера, рассматривая движение маховика отдельно от других тел системы.
Маховик совершает вращательное движении. Рассмотрим внешние силы. Помимо пары сил с моментом  , на него действуют реакция подшипника
, на него действуют реакция подшипника  и реакция кулисы
и реакция кулисы  . Система сил инерции приводится к паре с моментом
. Система сил инерции приводится к паре с моментом  , направленным против вращения, т.к. оно ускоренное (рис.3).
, направленным против вращения, т.к. оно ускоренное (рис.3).

Рис.3
Записывая условие уравновешенности плоской системы внешних сил

находим
 =
= 
При угле 
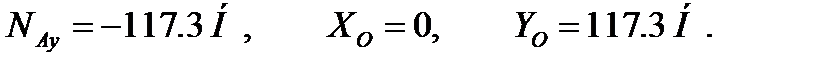
Сила  , приводящая в движение кулису, по третьему закону динамики равна реакции кулисы и направлена в противоположную сторону.
, приводящая в движение кулису, по третьему закону динамики равна реакции кулисы и направлена в противоположную сторону.