ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 15
По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ИССЛЕДОВАНИЕ ЧИСЛОВЫХ РЯДОВ НА СХОДИМОСТЬ. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННОЙ РЯД.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 15
По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ (2 курс)
Наименование работы: ИССЛЕДОВАНИЕ ЧИСЛОВЫХ РЯДОВ НА СХОДИМОСТЬ. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННОЙ РЯД.
1. Цель работы: Приобретение практических навыков исследования числового ряда на сходимость, используя основные признаки; умение разложить функцию в степенной ряд.
2. Литература:
2.1. В.А. Подольский, А.М. Суходольский «Сборник задач по математике» гл.13 §1-3 М.: Высшая школа, 1978 г.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме “Исследование числовых рядов на сходимость. Разложение функции в степенной ряд”.
3.2. Подготовить бланки отчета.
3.3. Подготовить ответы на вопросы допуска к работе:
3.3.1. Дать понятие числового ряда.
3.3.2. Что называется суммой ряда?
3.3.3. Сформулировать необходимый признак сходимости числового ряда.
3.3.4. Достаточный признак сходимости.
3.3.5. Признаки Даламбера, Коши.
3.3.6. Понятие знакочередующегося ряда.
3.3.7. Признак сравнения.
3.3.8. Понятие степенного ряда (функционального).
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:
5.1. Исследовать ряды на сходимость.
5.2. Разложить функцию в ряд Маклорена.
6. Порядок выполнения работы:
6.1. Записать задание своего варианта в отчет.
6.2. Исследовать ряды на сходимость.
6.3. Записать ответы, оформить отчет
6.4. Подготовить ответы на контрольные вопросы.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Результаты и ход выполнения работы.
7.4. Выводы, ответы.
8. Контрольные вопросы:
8.1. Дать понятие числового ряда.
8.2. Что называется суммой ряда?
8.3. Сформулировать необходимый признак сходимости числового ряда.
8.4. Достаточный признак сходимости.
8.5. Признаки Даламбера, Коши.
8.6. Понятие знакочередующегося ряда.
8.7. Признак сравнения.
8.8. Понятие степенного ряда (функционального).
8.9. Ряд Тейлора и ряд Маклорена.
9. Приложение:
Вариант 1.
1. а)  ; б) 
2. 
| Вариант 2.
1. а)  ; б) 
2. 
|
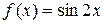
Вариант 3.
1. а)  ; б) 
2. 
| Вариант 4.
1. а)  ; б) 
2. 
|
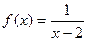
Вариант 5.
1. а)  ; б) 
2. 
| Вариант 6.
1. а) ; б) 
2. 
|
Вариант 7.
1. а)  ; б) 
2. 
| Вариант 8.
1. а)  ; б) 
2. 
|
10. Методические указания.
ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ.
Числовым рядом называется выражение вида
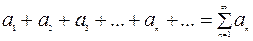
где числа a1,a2,a3, …, an, называемые членами ряда, образуют бесконечную последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
S1 = a1,
S2 = a1 + a2,
S3 = a1 + a2 + a3,
…………………..,
Sn = a1 + a2 + a3 +… + an
При n → ∞ имеет конечный предел: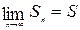 
. Этот предел называется суммой сходящегося ряда. Если 
не существует или бесконечен, то ряд называется расходящимся.
НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ РЯДОВ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ.
Ряд может сходится только при условии, что его общий член an при неограниченном увеличении номера n стремится к нулю: 
– это необходимый признак сходимости ряда.
Если же 
, то ряд расходится – это достаточный признак расходимости ряда.
ПРИЗНАК СРАВНЕНИЯ.
Если члены знакоположительного ряда
a1 + a2 + … + an + …, (1)
начиная с некоторого номера, не превосходят соответствующих членов ряда
b1 + b2 + … + bn …, (2)
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия
a + aq + aq2 + … + aqn + … (a > 0),
которая сходится при ׀q׀ < 1 и расходится при ׀q׀ >= 1, и гармонический ряд
1 + ½ + 1/3 + … + 1/n + …,
являющийся расходящимся рядом.
ПРИЗНАК ДАЛАМБЕРА.
Если для ряда (1) существует предел
то при l < 1 ряд сходится, при l > 1 – расходится (при l = 1 вопрос о сходимости ряда остается нерешенным).
РАДИКАЛЬНЫЙ ПРИЗНАК КОШИ.
Если для ряда (1) существует предел
то при q < 1 ряд сходится, при q > 1 – расходится (при q=1 вопрос о сходимости ряда остается открытым).