Имеется 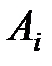 пунктов отправления
пунктов отправления 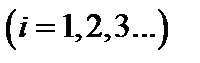 и
и 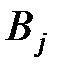 пунктов потребления
пунктов потребления 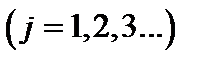 некоторого однородного товара. В каждом пункте отправления
некоторого однородного товара. В каждом пункте отправления 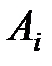 содержится запас товара объема
содержится запас товара объема 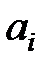 . Спрос
. Спрос 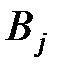 - го потребителя на поставку этого товара равен
- го потребителя на поставку этого товара равен 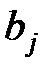 . Стоимость перевозки одной единицы груза из
. Стоимость перевозки одной единицы груза из 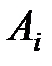 - го пункта отправления в
- го пункта отправления в 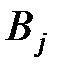 - й пункт потребления равна
- й пункт потребления равна 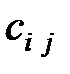 . Требуется спланировать перевозки так, чтобы их суммарная стоимость была наименьшей.
. Требуется спланировать перевозки так, чтобы их суммарная стоимость была наименьшей.
Исходные данные транспортной задачи обычно помещаются в таблицу стоимости перевозок.
| Поставщики | Потребители | Запасы поставщиков | |||
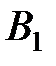
| …… | 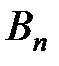
| |||
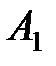
| 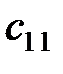
| …… | 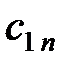
| 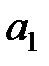
| |
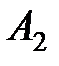
| 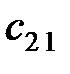
| ……. | 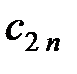
| 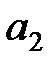
| |
| ………………. | …… | …… | …… | … | |
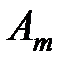
| 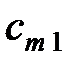
| …… | 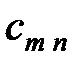
| 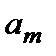
| |
| Спрос потребителей |
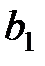
| …… |
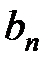
|
Когда суммарные запасы поставщиков равны общему спросу потребителей, т.е. 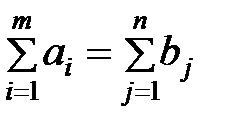 , транспортную задачу называют сбалансированной (закрытая модель).
, транспортную задачу называют сбалансированной (закрытая модель).
Если 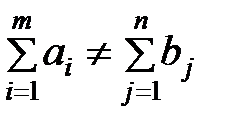 , транспортная задача называется несбалансированной (открытая модель).
, транспортная задача называется несбалансированной (открытая модель).
Решение несбалансированной задачи сводится к решению сбалансированной.
Пример. На трех базах 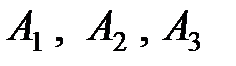 находится одинаковый груз в количестве 42, 30 и 28 тонн. Груз необходимо развести четырем потребителям
находится одинаковый груз в количестве 42, 30 и 28 тонн. Груз необходимо развести четырем потребителям 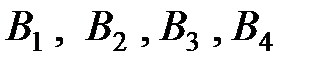 , потребности которых в данном грузе составляют 25, 23, 18 и 34 тонны соответственно. Стоимость перевозок задана матрицей тарифов
, потребности которых в данном грузе составляют 25, 23, 18 и 34 тонны соответственно. Стоимость перевозок задана матрицей тарифов 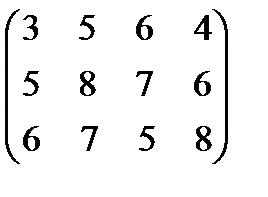 . Построить первоначальное распределение поставок.
. Построить первоначальное распределение поставок.
Решение. Запишем исходные данные в таблицу стоимости перевозок
| Постав-щики | Потребители | Запасы поставщиков | |||
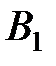
| 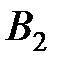
| 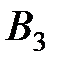
| 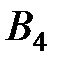
| ||
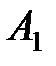
| |||||
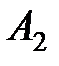
| |||||
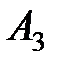
| |||||
| Спрос потребителей |
Метод потенциалов
В основе метода потенциалов лежит теорема, из которой следует, что
план 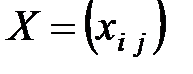 транспортной задачи является оптимальным тогда, и только тогда, когда существуют потенциалы поставщиков
транспортной задачи является оптимальным тогда, и только тогда, когда существуют потенциалы поставщиков 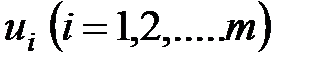 и потенциалы потребителей
и потенциалы потребителей 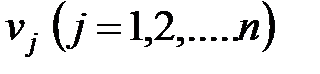 , для которых выполняются соотношения:
, для которых выполняются соотношения:
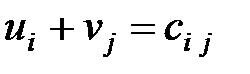 для клеток с ненулевыми поставками - заполненных
для клеток с ненулевыми поставками - заполненных 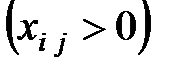 , (2)
, (2)
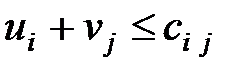 для клеток с нулевыми поставками - свободных
для клеток с нулевыми поставками - свободных 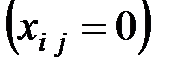 .
.
Проверяем оптимальность первого опорного плана, построенного по правилу минимальной стоимости, так как он дает меньшую стоимость перевозок. Введем в таблицу для первого опорного плана потенциалы следующим образом:
| Поставщики | Потребители | |||
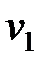 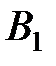
| 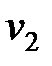 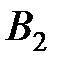
| 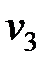
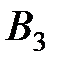
| 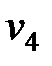
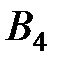
| |
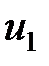 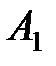
| - | - | ||
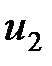 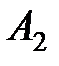
| - | - | ||
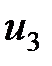 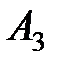
| - | - |
Вычислим значения введенных потенциалов, используя первое уравнение системы (2) для заполненных клеток таблицы (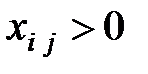 ):
):
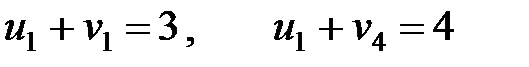 ,
,
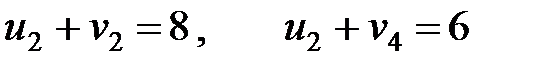 ,
,
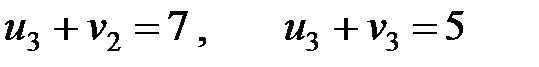 .
.
Получена система шести уравнений с семью неизвестными. Система решается следующим образом. Задается значение одной из неизвестных. Обычно считают 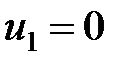 . Это позволяет определить остальные неизвестные
. Это позволяет определить остальные неизвестные
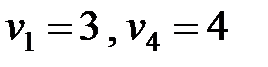 ,
, 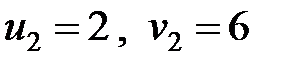 ,
, 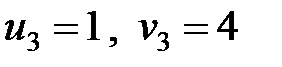 .
.
Проверим с помощью неравенства системы (2) опорный план на оптимальность.
Если обозначить 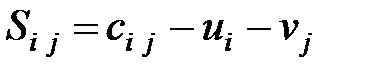 , то план оптимальный, если все
, то план оптимальный, если все  неотрицательны.
неотрицательны.
Неравенства записываются для свободных клеток таблицы 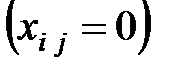 :
:
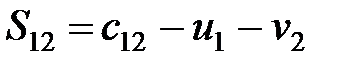
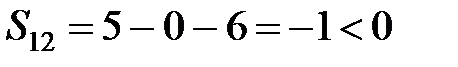 ,
,
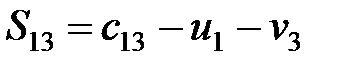
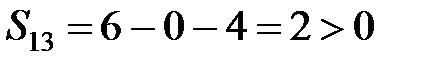 ,
,
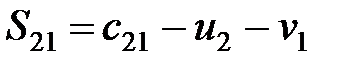
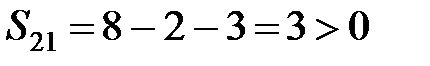 ,
,
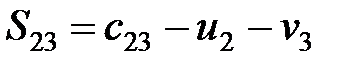
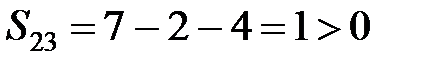 ,
,
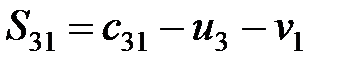
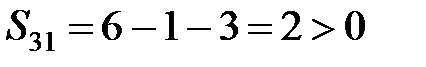 ,
,
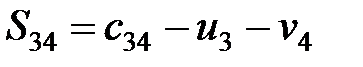
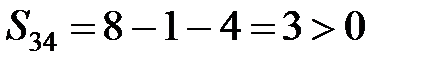 .
.
Так как 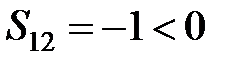 , одно из неравенств системы (2) не выполнено, следовательно, опорный план не является оптимальным. Требуется его улучшение, то есть перераспределение поставок.
, одно из неравенств системы (2) не выполнено, следовательно, опорный план не является оптимальным. Требуется его улучшение, то есть перераспределение поставок.
Для проведения процедуры оптимизации введем следующий цикл. Строим многоугольник с горизонтальными и вертикальными (!) сторонами, первая из вершин которого лежит в свободной клетке, имеющей наименьшее отрицательное значение 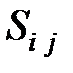 . Все остальные вершины лежат в заполненных клетках.
. Все остальные вершины лежат в заполненных клетках.
Когда в таблице ровно 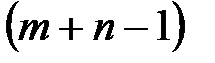 заполненных клеток, для каждой свободной клетки можно построить цикл, притом единственный. Перераспределение поставок происходит только в клетках, в которых лежат вершины цикла.
заполненных клеток, для каждой свободной клетки можно построить цикл, притом единственный. Перераспределение поставок происходит только в клетках, в которых лежат вершины цикла.
Каждой вершине цикла присваивается знак плюс или минус, причем вершина в свободной клетке всегда имеет знак +, знаки остальных вершин чередуются.
Из всех клеток с вершинами со знаком минус выбирается наименьшее значение перевозок, и на эту величину уменьшаются значения перевозок в клетках с «отрицательными вершинами», и увеличиваются в клетках с «положительными вершинами». Так как в цикле четное число вершин, общий объем перевозок в пределах цикла не меняется, что сохраняет баланс между запасами поставщиков и заявками потребителей.
В рассматриваемом примере, поскольку 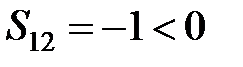 цикл начинается в клетке
цикл начинается в клетке 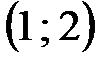 , следующие его вершины находятся в заполненных клетках
, следующие его вершины находятся в заполненных клетках 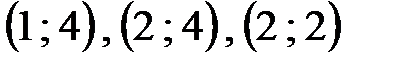 , после чего возвращаемся в клетку
, после чего возвращаемся в клетку 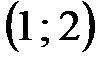 . Придаем знаки вершинам, как показано на рисунке
. Придаем знаки вершинам, как показано на рисунке
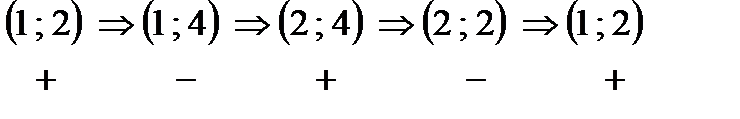
Данный цикл изображен на выше приведенной таблице.
Из клеток цикла с отрицательными вершинами выбираем клетку с наименьшей поставкой товара. Это клетка 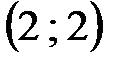 , и поставка в ней 13 тонн.
, и поставка в ней 13 тонн.
Пересчитываем таблицу поставок, добавляя 13 к поставкам в клетках с положительными вершинами и вычитая 13 из поставок в клетках с отрицательными вершинами. Таким образом,
В клетке 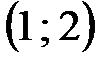 величина поставки станет 13 (0+13),
величина поставки станет 13 (0+13),
в клетке 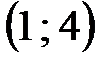 величина поставки станет 4 (17-13),
величина поставки станет 4 (17-13),
в клетке 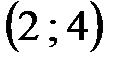 величина поставки станет 30 (17+13),
величина поставки станет 30 (17+13),
в клетке 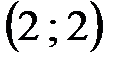 величина поставки 0 (13-13), и она становится свободной.
величина поставки 0 (13-13), и она становится свободной.
Внесем полученные результаты в таблицу:
| Поставщики | Потребители | |||
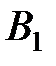
| 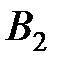
| 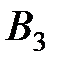
| 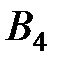
| |
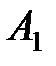
| - | |||
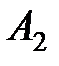
| - | - | - | |
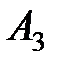
| - | - |
Количество заполненных клеток осталось 6 – план опорный.
Подсчитаем суммарные расходы на перевозки для полученного плана
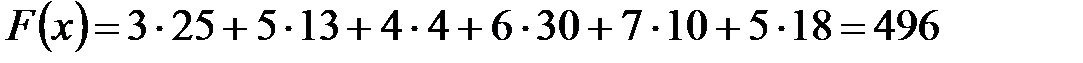 .
.
Они уменьшилась с 509 до 496.
Проверяем, является ли план оптимальным по той же схеме. Введем потенциалы
| Поставщики | Потребители | |||
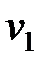 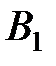
| 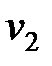 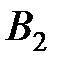
| 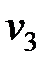
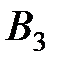
| 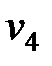
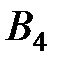
| |
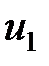 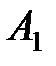
| - | |||
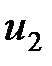 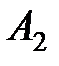
| - | - | - | |
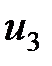 
| - | - |
Выполним первое условие из системы (2)
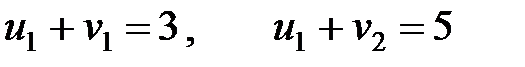 ,
,
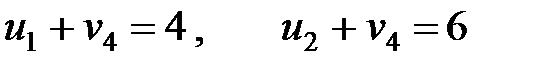 ,
,
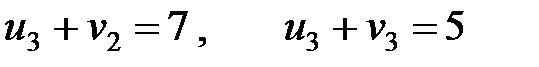 .
.
По аналогии решение системы
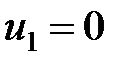 ,
, 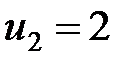 ,
, 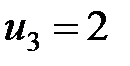 ,
, 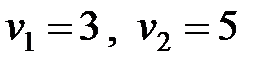 ,
, 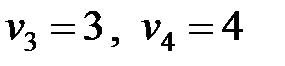 .
.
Из второго условия (2)
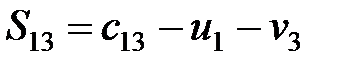
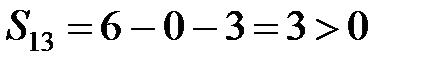 ,
,
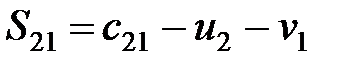
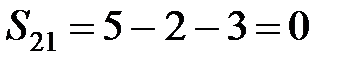 ,
,
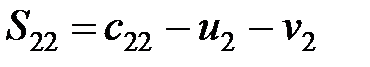
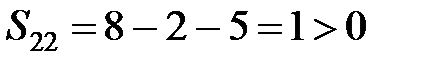 ,
,
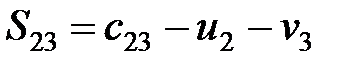
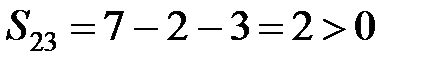 ,
,
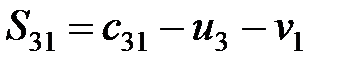
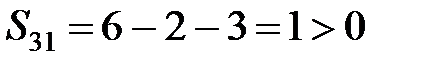 ,
,
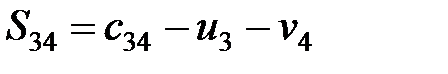
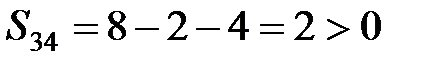 .
.
Все значения 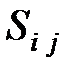 неотрицательны, полученный опорный план – оптимальный.
неотрицательны, полученный опорный план – оптимальный.
Примечание. Если некоторые из 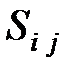 - отрицательные, процедуру оптимизации следует повторить.
- отрицательные, процедуру оптимизации следует повторить.
Ответ. Матрица оптимальных объемов перевозок
 ,
,
Минимальные суммарные расходы на перевозку 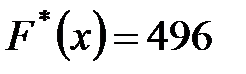 .
.

Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Казанский национальный исследовательский технологический университет»
(ФГБОУ ВО КНИТУ)
Высшая школа экономики
Кафедра Экономики, организации и управления производством
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ
для проведения промежуточной аттестации
по производственной практике
Экономика
(код и наименование направления подготовки/ специальности)