Рассмотрим конечную цепь Маркова с n состояниями, и пусть P – матрица переходных вероятностей, а E – единичная матрица размерности n.
Определение 14. Матрица λE – P называется характеристической матрицей данной цепи Маркова, а корни уравнения det(λE – P) = |λE – P| = 0 называются характеристическими числами матрицы.
Замечание. Из теории решения систем линейных уравнений известно, что для стохастической матрицы одно из характеристических чисел всегда равно 1, а остальные по модулю не превосходят 1.
Если цепь Маркова эргодична (существуют пределы элементов), то все остальные характеристические числа по модулю строго меньше 1.
Главные миноры Pjj матрицы λE – P при λ = 1 строго положительны.
Тогда предельные вероятности вычисляются по формулам:
Пример 6. P= 
λE – P = = 
|λE – P| = (λ – 0,7) ∙ (λ – 0,6) – 0,12 = λ2 – 1,3 λ + 0,3 = 0.
λ1 = 1, λ2 = 0,3.
P11(1) = 1 – 0,6 = 0,4, P22(1) = 1 – 0,7 = 0,3.
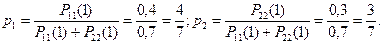
Упражнения
42. Доказать, что если цепь Маркова имеет, по крайней мере, одно несущественное состояние, то она не является эргодической.
43. Пусть цепь Маркова имеет, по крайней мере, 2 несообщающихся состояния. Доказать, что она не является эргодической.
В задачах 44–49 найти стационарное распределение, или доказать, что его не существует.
44. 
45. 
46. 
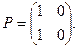
47. 
48. 
.
49. 
.
50. Эргодическая цепь Маркова имеет два состояния, известны предельные вероятности p и q. Найти матрицу вероятностей перехода за один шаг.
51. Показать, что у неэргодической марковской цепи может существовать стационарное распределение, причем единственное.
52. Доказать, что для конечной цепи Маркова всегда существует стационарное распределение.
53. Вероятность того, что будет дождь, если дождь был вчера, равна 0,7. Вероятность того, что будет дождь, если дождя вчера не было, равна 0,4. Найти предельную вероятность того, что будет дождь.
54. Два шахматиста, А и B, играют в турнире. Шахматист A выигрывает с вероятностью 0,3, проигрывает с вероятностью 0,2, делает ничью с вероятностью 0,5 независимо от результатов предыдущих игр. Для шахматиста B эти вероятности зависят от предшествующей игры. Если он выиграл предыдущую игру, то он выигрывает с вероятностью 0,4, а проигрывает с вероятностью 0,1. Если же он проиграл в предыдущей игре, то он выигрывает с вероятностью 0,2, а проигрывает с вероятностью 0,3. Если в прошлой игре была ничья, то вероятности у него такие же, как у А.
Кто из игроков наберет больше очков при длительной игре?
Дополнение (без доказательства)
Теорема 1. Эргодическая теорема (критерий эргодичности).
Для эргодичности марковской цепи необходимо и достаточно выполнение двух условий:
1) цепь неразложима и непериодична;
2) существует состояние ε0 такое, что время ξ возвращения в ε0 имеет конечное математическое Eξ.
Теорема 2. Эргодическая теорема Маркова.
Достаточное условие эргодичности однородной цепи с матрицей переходных вероятностей P: существует n, при котором все элементы матрицы Рn строго положительны.
Теорема 3. Неразложимая и непериодическая цепь Маркова с конечным числом состояний эргодична.
Теорема 4.
Если 
то при 
где 
– число возвращений системы в фиксированное состояние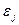 
за время n.
Следствие. Среднее время возвращения в состояние j в дискретные моменты t = 0, 1, 2, …равно Tj = 1/ pj, где pj предельная вероятность.
Напоминание.
Если цепь эргодична, то набор предельных вероятностей {pj} задает стационарное распределение и является (единственным) решением системы уравнений:
Смысл эргодичности: существуют вероятности попадания системы в состояние εj через большой промежуток времени, причем они не зависят от начального состояния системы.
Литература
1. Боровков А.А. Теория вероятностей. М.: Наука, 1976.
2. Вентцель А.Д. Теория случайных процессов. М.: Наука, 1975.
3. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы. М.: Изд-во МГТУ, 2000.
4. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов, М.:
Наука, 1977.
5. Крылов Н.В. Введение в теорию случайных процессов, М.: Изд-во МГУ, 1986.
6. Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика. М.: Наука, 1985.
Оглавление
1. Основные понятия. 2
Упражнения. 6
2. Классификация состояний. 7
Упражнения. 8
3. Классификация состояний в неразложимой цепи Маркова. 10
Упражнения. 13
4. Симметричное случайное блуждание. 14
Упражнения. 16
5. Теорема солидарности. 18
Упражнения. 20
6. Эргодичность и стационарные распределения. 21
Упражнения. 25
7. Литература. 26
Оглавление. 26