ЛОДУ второго порядка с постоянными коэффициентами

Частным случаем, рассмотренных выше ЛОДУ, являются ЛОДУ с постоянными коэффициентами.

Рассмотрим ЛОДУ второго порядка

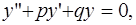(28)

где p, q – константы.

Для нахождения общего решения уравнения (28) достаточно найти два его частных решения, образующих фундаментальную систему.

Будем искать частные решения уравнения (28) в виде

y=e^kx, (29)

где k – некоторое число.

Дифференцируя функцию (29) два раза и подставляя выражения у, y', y" в уравнение (28), получим

k²e^kx+pke^kx+qe^kx =0,

т.к. , то на него разделим и получим характеристическое уравнение

k²+pk+q= 0, (30)

которое легко составляется по уравнению (28). Для этого достаточно в уравнении (28) заменить у, y', y" соответственно на k², k и 1.

При решении характеристического уравнения (30) возможны три случая.

Случай 1. Корни k₁ и k₂ – действительные и различные k₁ 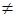k₂ 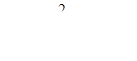. В этом случае частными решениями будут две функции , они образуют фундаментальную систему решений (линейно независимых), т.к. вронскиан 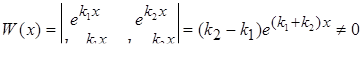. Следовательно, общее решение уравнения (28) имеет вид

у=с₁ +с₂ . (31)

Пример. Решить уравнение .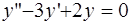

Решение. Составим характеристическое уравнение k²- 3 k +2=0. Найдем его корни 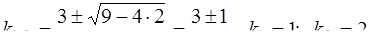Записываем общее решение по формуле (31)

у=с₁е^х+с₂е^2х, где с₁, с₂ – произвольные постоянные.

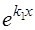Случай 2. Корни характеристического уравнения (30) действительные и равные: . В этом случае имеем одно частное решение у₁= . Покажем, что у₂=х является тоже решением уравнения (28). Подставим у ₂ в уравнение (28), имеем:

Частные решения у₁ и у₂ образуют фундаментальную систему решений: . Следовательно, в этом случае общее решение ЛОДУ (28) имеет вид

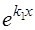у=с₁ +с₂ 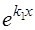x. (33)

Пример. Решить уравнение .

Решение. Составим характеристическое уравнение k²+ 4 k +4=0. Найдем его корни Записываем общее решение по формуле (33)

у=с₁е^-2х+с₂е^-2хx, где с₁, с₂ – произвольные постоянные.

Случай 3. Корни k₁ и k₂ уравнения (30) комплексные: ,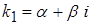

В этом случае частными решениями по формуле (29) будут функции

.

Найдем два действительных решения уравнения (28). Применяя формулы Эйлера получим:

Составим две линейные комбинации решений у₁ и у₂:

.

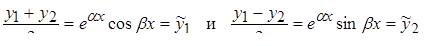Функции 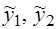являются решениями уравнения (28) и образуют фундаментальную систему решений, т.к. W (x)¹0 (убедитесь самостоятельно!) Поэтому общее решение уравнения (28) запишется в виде

у=с₁ +с₂ . (34)

Пример. Решить уравнение .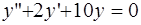

Решение. Составим характеристическое уравнение k²+ 2 k +10=0. Найдем его корни Записываем общее решение по формуле (34) у=с₁ +с₂ .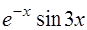

Структура общего решения уравнения второго порядка

Рассмотрим ЛНДУ второго порядка

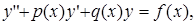(35)

где p(х), q(х), f(x) – заданные, непрерывные на (а;b) функции.

Уравнение

(36)

называется соответствующее уравнению (35) однородным.

Теорема (структура общего решения ЛНДУ). Общим решением уравнения (35) является сумма его произвольного частного решения и его общего решения соответствующего однородного уравнения (36), т.е.

у=у_оо+у_чн, (37)

где у_оо – общее решение уравнения (36), у_чн – частное решение уравнения (35).

Доказательство. Дифференцируя дважды равенство (37) и подставляя в уравнение (35), получим

или после преобразований имеем

Это означает, что функция (у_оо+у_чн) является решением уравнения (35).