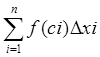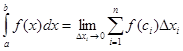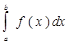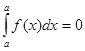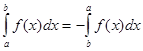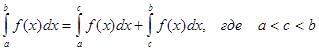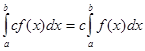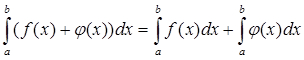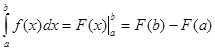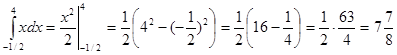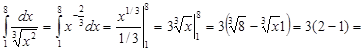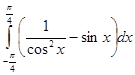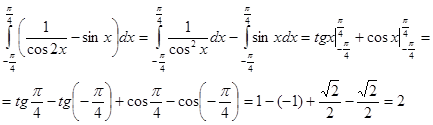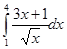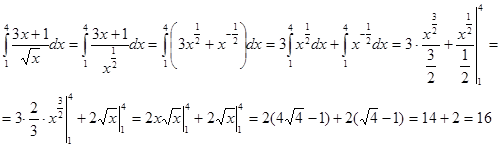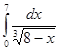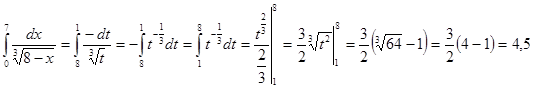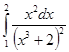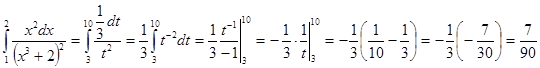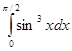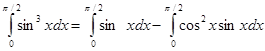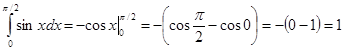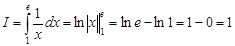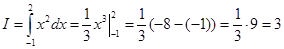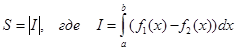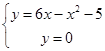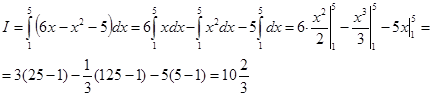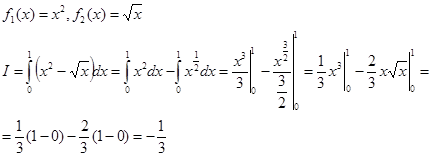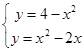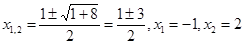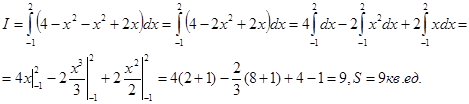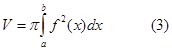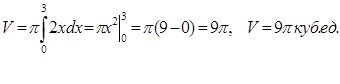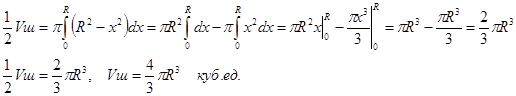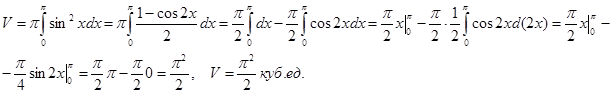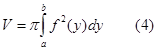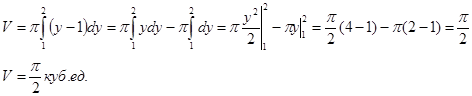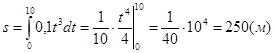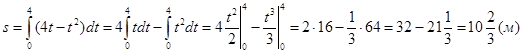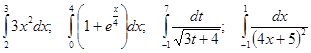Основные свойства определенного интеграла.

Понятие определенного интеграла.

Пусть функция f (x) определена на отрезке а£х£b. Допустим для простоты, что функция f(х) в указанном промежутке неотрицательна и a<b. Разобьем этот отрезок на n частей точками а=x_о<х₁<х₂<...<х_n=b. На каждом из частичных отрезков x_i-1£x£x_i (i=l, 2, 3,..., п) возьмем произвольную точку d и составим сумму:

f (ci) Dx1 + f (с₂) D х₂ + f (с₃) Dx₃ +.-.+ f (с„) D x_n =

Эта сумма носит название интегральной суммы функции f(x) на отрезке а £ х £ b.

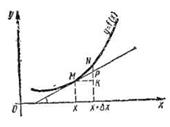
Рисунок – 52

Геометрически (рисунок - 52) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием D x_i и высотой f(c_t), а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.

Очевидно, что при всевозможных разбиениях отрезка а £ х £ b на части получим различные интегральные суммы, а следовательно, и различные «ступенчатые фигуры».

Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков Xi-1£x£Xi (i стремилась к нулю). Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления xi, ни от того, как выбираются промежуточные точки с_i,.

Этот предел и называется определенным интегралом от функции f(x) на отрезке а £ х £ b. Определенным интегралом от функции f(x) на отрезке а £ х £ b называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом òf(х) dx и читается «интеграл от а до b от функции f(x) дo dx» или, короче, «интеграл от а до bот f(x).,dx».

Число а называется нижним пределом интегрирования, число b - верхним; отрезок а £ х £ b - отрезком интегрирования.

Заметим, что всякая непрерывная на отрезке а £ х £ b функция f (x) интегрируема на этом отрезке.

Если интегрируемая на отрезке а £ х £ b функция f (x)b неотрицательна, то определенный интеграл численно равен площади S криволинейной трапеции аАВb, ограниченной графиком функции y=f(x), осью абсцисс и прямыми х=а и х=b (рисунок - 52), т.е.

В этом заключается геометрический смысл определенного интеграла.

Основные свойства определенного интеграла.

Все свойства сформулированы в предположении, что рассматриваемые функции интегрируемы в соответствующих промежутках.

1. Определенный интеграл с одинаковыми пределами равен нулю:

2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:

3. Отрезок интегрирования можно разбивать на части:

4. Постоянный множитель можно выносить за знак интеграла:

5. Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:

Непосредственное вычисление определенного интеграла.

Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона-Лейбница:

Т.е. определенный интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования.

Из этой формулы виден порядок вычисления определенного интеграла:

1. - найти неопределенный интеграл от данной функции;

2. - в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интеграла;

3. - из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.

Пример 1.

Вычислить интеграл

Пример 2.

Вычислить интеграл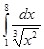

Решение:

Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:

=3

Пример 3. Вычислить интеграл

Решение:

Интеграл от разности функций заменим разностью интегралов от каждой функции:

Пример 4.

Вычислить интеграл

Решение:

Воспользуемся определением степени с дробным показателем, правилом деления суммы на число и вычислим определенный интеграл от каждого слагаемого отдельно:

Вычисление определенного интеграла методом подстановки.

Вычисление определенного интеграла методом подстановки состоит в следующем:

- часть подынтегральной функции заменить новой переменной;

- найти новые пределы определенного интеграла;

- найти дифференциал от обеих частей замены;

- все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);

- вычислить полученный определенный интеграл.

Пример 5.

Вычислить интеграл

Решение:

Введем подстановку 8-x=t, тогда -dx=dt, dx=-dt. Определим пределы интегрирования для переменной t. При х=0 получаем t_n=8-0=8, при х=7 получаем t_s=8-7=1,

Выразив подынтегральное выражение через t и dt и, перейдя к новым пределам, получим:

Пример 6.

Вычислить интеграл

Решение:

Произведем подстановку t³+2=t, тогда 3x²dx=dt, x²dx=(1/3)dt_- Определим пределы интегрирования для переменной t. При х=1 получаем t_н=1³+ 2=3, при х=2 получаем t_в=2³+2 = 10.

Выразив подынтегральное выражение через t и dt и, перейдя к новым пределам, получим:

Пример 7.

Вычислить интеграл

Решение:

Положим cosx=t, тогда -sinxdx=dt и sinxdx=-dt. Определим пределы интегрирования для переменной t: t_н=cos0=l, t_в =cos (p/2) =0.

Выразив подынтегральное выражение через t и dt и, перейдя к новым пределам, получим:

Пример 9.

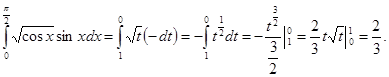
Вычислить интеграл

Решение:

Сначала преобразуем подынтегральное выражение:

sin³x = sin²x*sin x = (1 - cos²x) sin x = sin x - cos²x sinx.

Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:

Вычислим каждый интеграл отдельно:

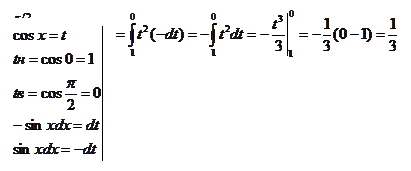Приложения определенного интеграла.

Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.

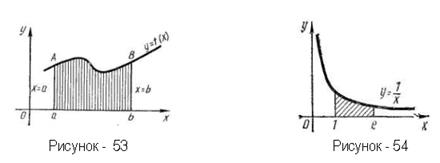
Площади плоских фигур. Площадь криволинейной трапеции аАВb (рисунок - 53), ограниченной графиком непрерывной функции y=f(x) (где а<х<b), отрезком ab оси Ох и отрезками прямых х=а и х=b, вычисляется по формуле:

б

S = |I|, где I=ò f(x)dx. (1)

а

Пример 10.

Вычислить площадь фигуры, ограниченной гиперболой ху=1, осью Ох и прямыми х=1 и х=е.

Решение:

Применяя формулу (1), получаем:

S=1 кв.ед.

Пример 11. Вычислить площадь фигуры, ограниченной параболой у=х², прямыми х= -1, х=2 и осью абсцисс (рисунок - 55).

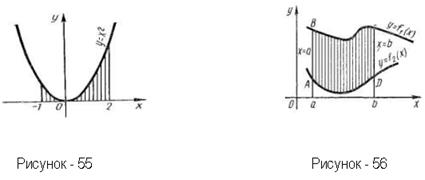
Решение: Применяя формулу (1), получаем:

S=3 кв.ед.

Площадь фигуры ABCD (рисунок - 56), ограниченной графиками непрерывных функций y=f(x) и y=U(x) (где а<х<b) и отрезками прямых х=а и х=b, вычисляется

по формуле:

Пример 12. Вычислить площадь фигуры, ограниченной кривой у=6х-х²-5 и осью Ох (рисунок - 57).

Решение:

Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций y=6х-х2-5 и у = 0 (ось Ох). Для этого решим систему:

Имеем 6x-х²-5 = 0, х²-6х + 5=0, x₁,₂=3±Ö 9-5 = 3±2; x₁ = 1, x₂ = 5.

Теперь найдем искомую площадь по формуле (2):

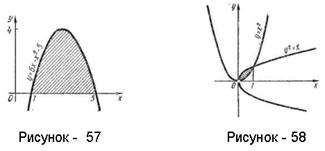
Пример 13. Вычислить площадь фигуры, ограниченной линиями у=х² и у²=х (рисунок - 58).

Решение:

Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций у=х² и у²=х.

Для этого решим систему

Имеем (х²)²=х, х⁴-х=0, х(х³-1)=0, x₁=0, х₂=1. Искомую площадь вычисляем по формуле (2) при:

S=III=1/3 кв.ед.

Пример 14. Вычислить площадь фигуры, ограниченной параболами у=4-х² и у=х² - 2х (рисунок - 59).

Решение:

Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций у=4- х² и у=х² - 2х.

Для этого решим систему

Имеем 4-х²=х²-2х, 2х²- 2x-4=0, х²-х- 2=0,

Искомую площадь вычисляем по формуле (2):

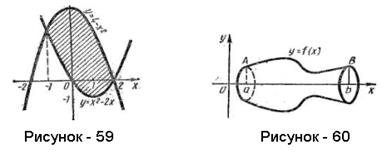
Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции аАВb, ограниченной непрерывной кривой y=f(x) (где а<х<b), отрезком аb оси Ох и отрезками прямых х=а и х=b (рисунок - 60), вычисляется по формуле:

Пример 15. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой у²=2х, прямой х=3 и осью Ох (рисунок - 61).

Решение:

Применяя формулу (3), находим:

Пример 16.

Вычислить объем шара радиуса R (рисунок - 62).

Решение:

Шар образован вращением вокруг оси Ох круга, ограниченного окружностью x²+y²=R² с центром в начале координат и радиусом R. Учитывая симметрию круга относительно оси ординат, сначала найдем по формуле (3 половину искомого объема:

Пример 17. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной осью Ох и полуволной синусоиды y=sinx (0£x£p) (рисунок - 63).

Решение:

Применяя формулу (3), находим:

Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции аАВb, ограниченной непрерывной кривой x=f(y) (где а£x£b),отрезком ab оси Оу и отрезками прямых у=а и у=b (рисунок - 64), вычисляется по формуле:

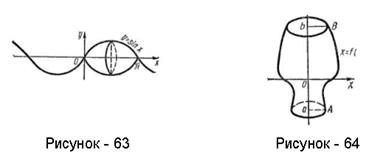
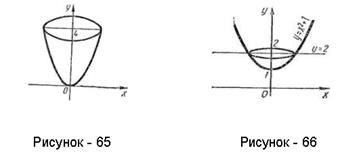
Пример 18. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой у=х² и прямой у=4 (рисунок - 65).

Решение:

Применяя формулу (4), находим:

Пример 19. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой у=х²+1 и прямой у=2 (рисунок - 66).

Решение:

Объем полученного тела (оно называется параболоидом) вычислим по формуле (4):

Путь, пройденный точкой. Если точка движется прямолинейно и ее скорость v=f[t), есть известная функция времени t, то путь, пройденный точкой за промежуток времени t₁ £t £t₂, вычисляется по формуле (5):

Пример 20. Тело движется прямолинейно со скоростью v=0,1t³ (v - в м/с). Вычислить путь, пройденный телом за 10 с.

Решение:

Применяя формулу (5), находим:

Пример 21. Скорость прямолинейно движущегося тела равна v = (4t-t²) (v - в м/с). Вычислить путь, пройденный телом от начала движения до остановки.

Решение.

В момент остановки скорость движения тела равна нулю, т.е. 4t-t² = 0, t(4-t) =0, t1 = 0, t₂=4.

Итак, тело остановится через 4 с.

Путь, пройденный телом за это время, вычисляем по формуле (5):

Вопросы и упражнения для самоконтроля:

1. Дайте определение определенного интеграла.

2. Перечислите основные свойства определенного интеграла.

3. В чем заключается геометрический смысл определенного интеграла?

4. Напишите формулы для определения площади плоской фигуры с помощью определенного интеграла.

5. По каким формулам находится объем тела вращения?

6. Напишите формулу для вычисления пути, пройденного телом.

7. Напишите формулу для вычисления работы переменной силы.

8. Вычислите определенные интегралы:

9. Вычислите площадь фигуры, ограниченной линиями: а) у=х²+1, у = 0, х=-2, х=1; б) х²- 9у=0 и x - Зу + 6=0.

10. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой у²=х, прямой х=2 и осью Ох.

11. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой у²=х, прямыми у=1, у=4 и осью Оу.

12. Тело движется прямолинейно со скоростью v= (2+4t³) (v - в м/с). Вычислите путь, пройденный телом за первые три секунды.

14. Какую работу нужно совершить, чтобы растянуть пружину на 6 см, если сила в 1 Н растягивает ее на 1 см?

15. Вычислите силу давления воды на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м.

Ответы. 9. а) 19; б) 4е; в) 8/3: г) 2/9.10. а) 6 кв.ед.; б) 13,5 кв. ед., 11. 2л куб..

Основные свойства определенного интеграла.

Поиск по сайту