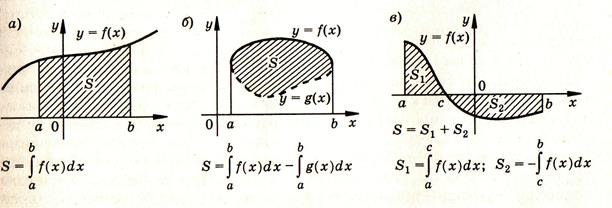Определенный интеграл и его свойства.
Формула Ньютона – Лейбница.
Вычисление площадей плоских фигур.
I. Определенный интеграл и его свойства.
Задача, которая приводит к понятию определенного интеграла.
Пусть на отрезке  определена непрерывная и неотрицательная функция
определена непрерывная и неотрицательная функция  .
.
Определение. Криволинейной трапецией называется часть плоскости, ограниченная графиком функции 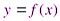 , осью Ох (
, осью Ох ( ) и отрезками прямых
) и отрезками прямых 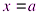 ,
,  .
.
П  усть требуется найти площадь криволинейной трапеции.
усть требуется найти площадь криволинейной трапеции.
Для этого разобьём отрезок  точками
точками  на n частичных отрезков и положим
на n частичных отрезков и положим 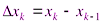 ,
, 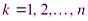 . Наибольшую из этих разностей обозначим через
. Наибольшую из этих разностей обозначим через  :
:  . На каждом частичном отрезке
. На каждом частичном отрезке 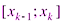 выберем произвольную точку
выберем произвольную точку  :
:  . Произведение
. Произведение  даст площадь прямоугольника с основанием
даст площадь прямоугольника с основанием  и высотой
и высотой  , тогда приближённо площадь
, тогда приближённо площадь  криволинейной трапеции
криволинейной трапеции  равна сумме:
равна сумме:
 ,
, 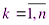 .
.
Эта сумма называется интегральной суммой.
Если увеличить количество частичных отрезков так, что длина любого из них будет стремиться к нулю, то данная интегральная сумма будет стремиться к площади 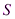 криволинейной трапеции:
криволинейной трапеции:
 ,
,  . (1)
. (1)
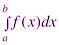 Определение. Если предел (1) интегральной суммы существует, не зависит от способа разбиения отрезка
Определение. Если предел (1) интегральной суммы существует, не зависит от способа разбиения отрезка  на части и от выбора точек
на части и от выбора точек  в них, то этот предел называется определённым интегралом отфункции
в них, то этот предел называется определённым интегралом отфункции  на отрезке
на отрезке 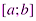 и обозначается:
и обозначается:
Таким образом,
 .
.
При этом функция  называется подынтегральной функцией,
называется подынтегральной функцией, 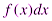 – подынтегральным выражением, числа a и b – пределами интегрирования (a – нижний граница, b – верхний граеица), x - переменной интегрирования.
– подынтегральным выражением, числа a и b – пределами интегрирования (a – нижний граница, b – верхний граеица), x - переменной интегрирования.
Определение. Функция  , для которой на отрезке
, для которой на отрезке 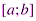 существует определенный интеграл
существует определенный интеграл 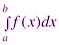 , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Геометрический смысл определенного интеграла: если функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  , то
, то 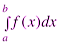 геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции
геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции  , снизу – отрезком
, снизу – отрезком 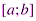 оси
оси  , с боков – отрезками прямых
, с боков – отрезками прямых  ,
, 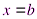 .
.
Свойства определённого интеграла
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию  интегрируемой на отрезке
интегрируемой на отрезке 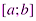 .
.
1. При перестановке пределов интегрирования знак определённого интеграла изменяется:
 .
.
2. Определённый интеграл от функции с равными пределами интегрирования равен нулю:
 .
.
3. Постоянный множитель можно вынести за знак определённого интеграла:
 ,
, 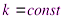 .
.
4. Определённый интеграл от алгебраической суммы двух функций равен алгебраической сумме определённых интегралов от этих функций:
 .
.
5. Определённый интеграл по отрезку равен сумме определённых интегралов по его частям:
 , где
, где  .
.
6. Если функция  - чётная на отрезке
- чётная на отрезке  , то выполняется равенство
, то выполняется равенство
 .
.
7. Если функция  - нечётная на отрезке
- нечётная на отрезке  , то выполняется равенство
, то выполняется равенство
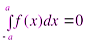 .
.
II. Формула Ньютона – Лейбница.
Теорема.
Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и  – первообразная функции
– первообразная функции  на этом отрезке, то имеет место формула Ньютона–Лейбница:
на этом отрезке, то имеет место формула Ньютона–Лейбница:
 .
.
Эта формула позволяет вычислить определённый интеграл, зная какую-либо первообразную для интегрируемой функции. Первообразную для функции  можно найти, вычисляя неопределённый интеграл от этой функции.
можно найти, вычисляя неопределённый интеграл от этой функции.
 Замечание.
Замечание.
Для краткости записи употребляется обозначение:
Таким образом,
определенный интеграл – это разность между значением первообразной в верхней и нижней границах, т. е. как F (b) - F (a):
 .
.
Алгоритм вычисления определенного интеграла:
1. Найти соответствующий определенный интеграл используя свойства и формулы интегрирования, т.е неопределенный интеграл (не приписывая константу С).
2. Подставить в получившуюся первообразную верхнюю границу, затем нижнюю границу, а между ними знак «-».
3. Вычислить.
В результате вычисления определенного интеграла, получается число.
ПРИМЕРЫ. Вычислить определенный интеграл
1) 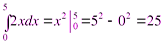 .
.
 2)
2) 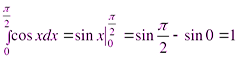 .
.
3)
Решение:

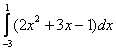 4)
4)
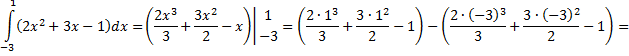
 .
.
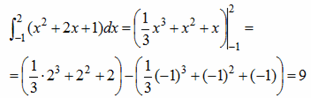
5)
III. Вычисление площадей плоских фигур.


Возможны следующие случаи: