Б класс. ТЕМА «ВЕКТОРЫВ ПРОСТРАНСТВЕ»
Урок 5. Компланарные векторы Дата: 19.11.21
Вспомните:
1) Что называется вектором в пространстве и как его обозначают?
2) Какой вектор называется нулевым и как он обозначается?
3) Что называется длиной вектора и как ее обозначают?
4) Какие векторы называются коллинеарными?
5) Какие векторы называются сонаправленными и как они обозначаются?
6) Какие векторы называются противоположнонаправленными и как они обозначаются?
7) Какие векторы называются равными?
Посмотрите презентацию.
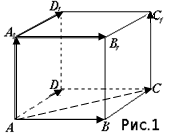 Давайте рассмотрим рисунок. Сравните тройки векторов (
Давайте рассмотрим рисунок. Сравните тройки векторов ( ) и (
) и ( ). Выделите общее и различное между этими двумя тройками векторов.
). Выделите общее и различное между этими двумя тройками векторов.
( Обе тройки векторов отложены от одной и той же точки. Первые три вектора лежат в одной плоскости. Векторы  не лежат в одной плоскости.)
не лежат в одной плоскости.)
Теперь сравните тройки векторов (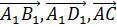 ) и (
) и (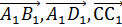 ). Что вы можете сказать о них? (Если эти векторы отложить от одной точки, то мы получим векторы (
). Что вы можете сказать о них? (Если эти векторы отложить от одной точки, то мы получим векторы ( ) и (
) и ( ), где (
), где ( ) лежат в одной плоскости, а (
) лежат в одной плоскости, а ( ) не лежат в одной плоскости)
) не лежат в одной плоскости)
Тройки векторов  и (
и (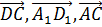 ) называют тройками компланарных векторов, а тройки векторов
) называют тройками компланарных векторов, а тройки векторов  и (
и (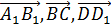 ) не задают компланарных векторов.
) не задают компланарных векторов.
Самое время познакомиться с существенным и одним из главных отличий векторов на плоскости и векторов в пространстве – понятие компланарных векторов.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
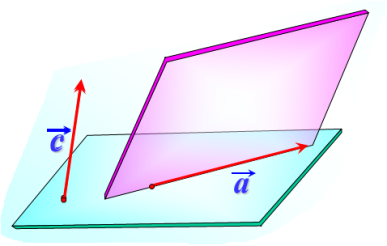 Другими словами, векторы называются компланарными, если имеют равные им векторы, лежащие в одной плоскости.
Другими словами, векторы называются компланарными, если имеют равные им векторы, лежащие в одной плоскости.
Любые два вектора компланарны.
Если рассмотреть три вектора, то они могут быть как компланарными, так и некомпланарными.
В каком случае они будут компланарными?
 Изобразим этот случай.
Изобразим этот случай.
Тогда через один из коллинеарных векторов и вектор не коллинеарный ему можно провести плоскость. А для второго из коллинеарных векторов можно изобразить равный в этой плоскости.
Так мы получаем, что два вектора всегда будут компланарными, а три вектора будут компланарными, если среди них есть пара коллинеарных векторов.
Задача.
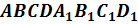 – прямоугольный параллелепипед. Компланарны ли векторы
– прямоугольный параллелепипед. Компланарны ли векторы  ?
?
Решение. Через векторы  проведем плоскость
проведем плоскость 

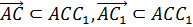 ,
, 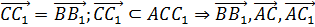 – компланарны
– компланарны
В данном задании мы, пользуясь определением, выяснили компланарны данные тройки векторов или нет.
Также существует признак компланарности трех векторов.
Если вектор 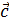 можно разложить по векторам
можно разложить по векторам 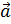 и
и 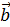 , т.е. представить в виде
, т.е. представить в виде 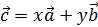 , где
, где 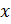 и
и 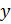 – некоторые числа, то векторы
– некоторые числа, то векторы  компланарны.
компланарны.
Давайте докажем данный признак.

Векторы  не коллинеарны (если векторы коллинеарны, то компланарность векторов
не коллинеарны (если векторы коллинеарны, то компланарность векторов  очевидна).
очевидна).
Отложим от произвольной точки 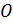 векторы
векторы 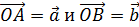 (рис).
(рис).
Векторы 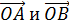 лежат в плоскости
лежат в плоскости 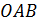 . В этой же плоскости лежат векторы
. В этой же плоскости лежат векторы  , следовательно и их сумма – вектор
, следовательно и их сумма – вектор  , равный вектору
, равный вектору 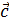 .
.
Итак, векторы 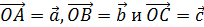 лежат в одной плоскости, т.е. векторы
лежат в одной плоскости, т.е. векторы  компланарны.
компланарны.
Также справедливо и обратное утверждение: Если векторы  компланарны, а векторы
компланарны, а векторы 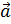 и
и 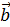 не коллинеарны, то вектор
не коллинеарны, то вектор 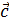 можно разложить по векторам
можно разложить по векторам 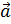 и
и 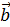 , причем коэффициенты разложения определяются единственным образом.
, причем коэффициенты разложения определяются единственным образом.
Докажите его самостоятельно дома.
Закрепление нового материала
| Компланарные векторы | |
| Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости | |
| Т.1: Любые два вектора компланарны | |
| Т.2: три вектора, среди которых имеется два коллинеарных, так же компланарны | |
| Признак компланарности трех векторов | Свойство трех компланарных векторов |
Если вектор 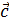 можно разложить по векторам можно разложить по векторам 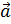 и и 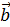 , то есть представить в виде: , то есть представить в виде: 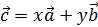 (х, у - некоторые числа), то векторы (х, у - некоторые числа), то векторы 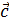 , , 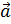 и и 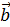 - компланарны. - компланарны.
| Если векторы 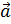 , ,  компланарны, а векторы компланарны, а векторы 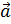 и и 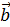 не коллинеарны, то вектор не коллинеарны, то вектор 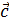 можно разложить по векторам можно разложить по векторам 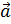 и и 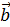 , причем коэффициенты разложения определяются единственным образом , причем коэффициенты разложения определяются единственным образом
|
Рассмотреть задачу на слайдах 5-8.
Решение упражнений по теме.
Решить № 355 (решение на слайдах 10-12)
Домашнее задание: П.43 учить определения, доказать обратное утверждение признака компланарности трех векторов. Вопросы к главе: № 13-15, выполнить № 357, № 374.