Решение биквадратного уравнения методом замены переменной

Занятие № 9. Равносильные уравнения и неравенства.

(Квадратные уравнения и сводящиеся к ним.)

План.

Исследование корней квадратного уравнения по дискриминанту. Приведенное квадратное уравнение.

Уравнения, сводящиеся к квадратным.

Исследование корней квадратного уравнения по дискриминанту. Приведенное квадратное уравнение.

 

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

 

Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.

 

Определение

 

Уравнение вида ax² + bx + c = 0, где a, b, c - действительные числа, причем a ≠ 0, называют квадратным уравнением.

 

Если a = 1, то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным.

Числа a, b, c носят следующие названия: a - первый коэффициент, b - второй коэффициент, c - свободный член.

Если хотя бы одно из чисел b или с равно нулю, то квадратное уравнение называется неполным, если же числа b и с отличны от нуля — полным.

НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ

Ø ах² + с = 0, b = 0, с≠0.

,

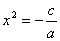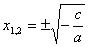
Ø ах² + bx = 0, b ≠0, с=0

Имеем х(ах + b) = 0;

x=0 или .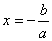

Ø ах² = 0, b =0, с=0.

Имеем х = 0.

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения - проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

1. c = 0, то уравнение примет вид

ax² + bx = 0.

x(ax + b) = 0,

x = 0 или ax + b = 0, x = -b: a.

2. b = 0, то уравнение примет вид

ax² + c = 0,

x₂ = -c / a,

x_{1, 2} = ±√(-c / a).

3. b = 0 и c = 0, то уравнение примет вид

ax² = 0, x = 0

 

Решение неполного квадратного уравнения

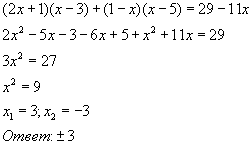
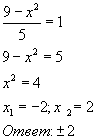
ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ

Корни уравнения ах² + bх + с =0 находят по формуле

Если D = b² - 4ас > 0, то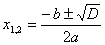

Если D = 0, то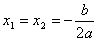

Если D < 0, то корней нет.

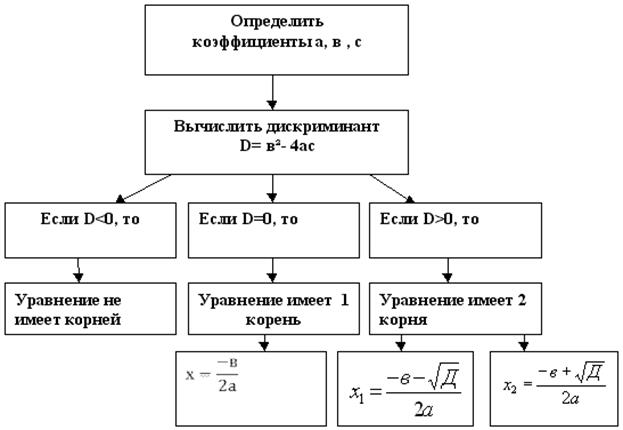
Решение полных уравнений

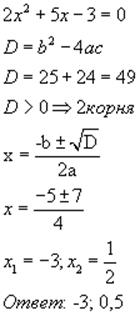
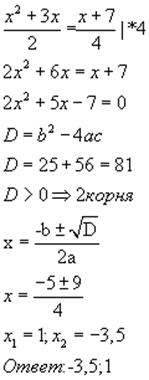
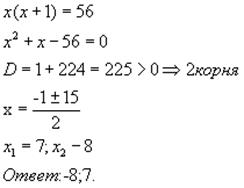
Приведенное квадратное уравнение — уравне­ние вида

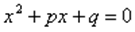,у которого первый коэффициент равен a=1.

Ø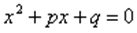

ü Если D = р² – 4q > 0, то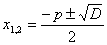

ü Если D = 0, то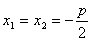

ü Если D < 0, то корней нет.

Теорема Виета

Если х₁ и х₂ — корни приведенного квадрат­ного уравнения 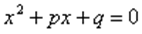, то

, .

 

 

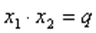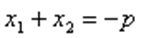Уравнения, сводящиеся к квадратным.

 

Уравнения высших степеней, сводящиеся к квадратным, — уравнения, которые с помощью ал­гебраических преобразований или замены перемен­ной можно свести к виду, а ах² + bх + с =0,, где а ≠ 0.

Би …- часть сложных слов, обозначающая: состоящий из двух частей, имеющий два признака, взятый дважды (бицепс).

Биквадратное уравнение — уравнение вида

ах⁴ + bх² + с =0, где а ≠ 0

являющееся квадратным относительно 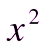, называется биквадратным уравнением и решается методом замены переменной ().

Решение биквадратного уравнения методом замены переменной

1. Вводят переменную х² = у.

2. Подставить данную переменную в исходное уравнение. Получают квадратное уравнение вида

ay² + by + с = 0.

3. Решить квадратное уравнение относительно новой переменной.

4. Если в квадратном уравнении дискрими­нант D = b² - 4ас < 0, то это квадратное, а значит, и биквадратное уравнение не имеют корней.

4. Если D = 0, то биквадратное уравнение имеет вид 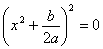(где а ≠ 0).

Тогда решение биквадратного уравнения сводится к решению неполного квадратного уравнения 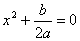(которое может либо не иметь корней, либо иметь два корня).

5. Если D > 0, то х² = y₁ или х² = у₂, где y _l и y₂ — корни квадратного уравнения. Тогда ре­шение биквадратного уравнения сводится к ре­шению двух неполных квадратных уравнений (в этом случае биквадратное уравнение может не иметь корней, иметь два или четыре корня).

 

Пример 1.

1. Выполнить замену 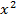= t.

2. Решить квадратное уравнение.

3. Выполнить обратную замену.

4. Записать ответ.

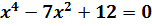
1. ,

 

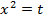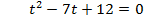
2.

 

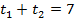
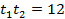
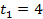
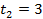
3.

 

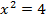
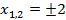
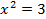
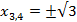
4. Ответ: -2, 2,

 

Пример 2.

 

 

 

Пример 3.

Пример 4.

Решите уравнение:

.

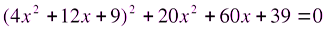Решение. Данное уравнение сводится к квадратному путем замены переменной. Запишем уравнение в виде

;

.

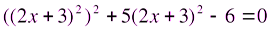Пусть 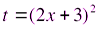, , 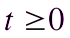тогда

.

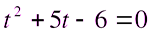Решая, последнее уравнение найдем , , 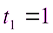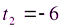(не подходит, так как 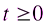). Вернемся к переменной .

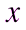Из уравнения 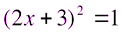получим:

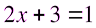или .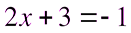

Откуда , .

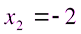Ответ: -1; -2.

 

Пример 5.

 

Пример 6.

Решите уравнение:

.

Решение. Заметим, что 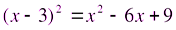. Тогда

;

.

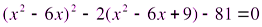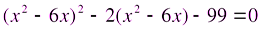Пусть 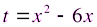, тогда

.

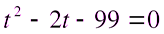Решая, последнее уравнение найдем:

,

, .

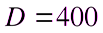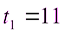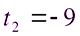Вернемся к переменной .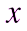

 

1) ;

, ;

 

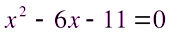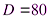
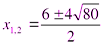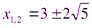2) ;

,

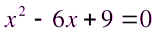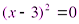Ответ: , .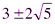

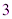Пример 7.

Решите уравнение:

.

 

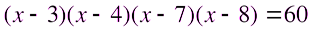Решение. Преобразуем уравнение к виду

.

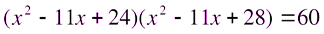Пусть 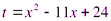, тогда , , , , .

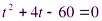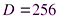Возвращаясь к переменной 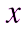, получим

, , , ,

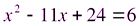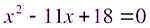или

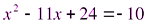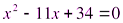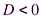, , - решений нет.

Ответ: , .

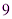Указание: сгруппировать сомножители попарно (подобрать удачный способ группировки), представить левую часть в виде произведения двух квадратных трехчленов, а затем производить замену переменной.

 

Пример 8.

Решите уравнение (х ² – 5 х + 4) (х ² – 5 х + 6) = 120.

Решение. В левой части уравнения переменная х входит только в выражение х² – 5х, которое встречается в уравнении дважды. Это позволяет решить данное уравнение с помощью введения новой переменной. Обозначим х² – 5х через у:

х² – 5х = у.

Тогда уравнение сведется к уравнению с переменной у:

(у + 4 )(у + 6 ) = 120,

которое после упрощения примет вид:

(у + 4 )(у + 6 ) = 120

у² + 4 у + 6 у + 24 – 120 = 0

у² + 10 у – 96 = 0.

Решим получившееся уравнение:

у₁ + у₂ = - 10;

у₁ · у₂ = - 96.

у₁ = - 16; у₂ = 6.

Отсюда

1. х² – 5х = - 16;

х² – 5х + 16 = 0 - корней нет.

 

2. х² – 5х = 6;

х² – 5х – 6 = 0

x₁ + x₂ = 5; x₁ = - 1;

x₁ · x₂ = - 6. x₂ = 6.

 

Ответ: x₁ = - 1; x₂ = 6.