Практическое занятие № 1
«Действия над матрицами. Вычисление определителей»
1. Цель: Выработать навыки и умения у студентов в решении задач на действия с
матрицами
2. Пояснения к работе:
Краткие теоретические сведения
Матрицы
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

или, сокращенно,  где
где  (т.е.
(т.е.  ) – номер строки,
) – номер строки,  (т.е.
(т.е.  ) - номер столбца. Матрицу
) - номер столбца. Матрицу  называют матрицей размера
называют матрицей размера  и пишут
и пишут  . Числа
. Числа  , составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ. Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.
, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ. Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.  если
если  где
где 

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера  называют матрицей
называют матрицей  - го порядка.Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Матрица, содержащая всего один столбец или одну строку называется вектором (или вектор- столбец, или вектор-строка соответственно). Их вид
- го порядка.Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Матрица, содержащая всего один столбец или одну строку называется вектором (или вектор- столбец, или вектор-строка соответственно). Их вид 
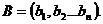 Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается  . Так, если
. Так, если  то
то 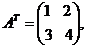 если
если  то
то  Транспонированной матрица обладает следующим свойством:
Транспонированной матрица обладает следующим свойством: 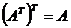 .
.
2.1.2 Действия над матрицами
Сложение. Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц  и
и  называется матрица
называется матрица 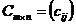 такая, что
такая, что
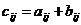 (
( ,
,  ).
).
Пример 1.  . Аналогично определяется разность матриц.
. Аналогично определяется разность матриц.
Умножение матрицы на число. Произведением матрицы  на число k называется матрица
на число k называется матрица  такая, что
такая, что 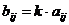 (
( ,
,  ).
).
Пример. 
Матрица  называется противоположной матрице А. Разность матриц А-В можно определить так: А-В =А+(-В). Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
называется противоположной матрице А. Разность матриц А-В можно определить так: А-В =А+(-В). Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1.  5.
5. 
2.  6.
6. 
3.  7.
7. 
4.  8.
8. 
где A, B, C – матрицы,  и
и  - числа.
- числа.
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической.
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица 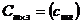 такая, что
такая, что
 , где
, где  ,
, 
т. е. элемент i -й строки и k -го столбца матрицы произведения С равен сумме произведений
элементов i -й строки матрицы А на соответствующие элементы k -го столбца матрицы В.
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют.
Пример 2.  . Тогда произведение
. Тогда произведение  не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение
не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение  , которое считают следующим образом:
, которое считают следующим образом:

Умножение матриц обладает следующими свойствами:
1.  3.
3. 
2. 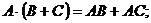 4.
4. 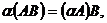
2.1.3 Определитель матрицы
Квадратной матрице А порядка n можно сопоставить число det А (или  , или
, или  ), называемое ее определителем, следующим образом
), называемое ее определителем, следующим образом
1. 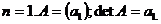
2. 
3. 

Пример 3. Найти определитель матрицы 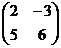 .
.
Решение: 
Пример. Вычислить определитель

Ответ: D=4.
2.1.4 Свойства определителей
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.
Иными словами,

В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак
определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Свойство 6. («Элементарные преобразования определителей»). Определитель не изменится, если
к элементам одного ряда прибавить соответствующие элементы параллельного ряда,
умноженные на любое число.
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения. Минором некоторого элемента  определителя n -го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
определителя n -го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  . Так если
. Так если
 то
то 

Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «плюс», если сумма
определителя называется его минор, взятый со знаком «плюс», если сумма  четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.
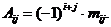
Свойство 7. («Разложение определителя по элементам некоторого ряда»).
Определитель равен сумме произведений элементов некоторого ряда на соответствующие им
алгебраические дополнения. В случае определителей 3-го порядка свойство 7 означает, что
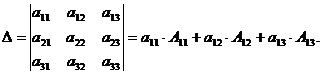
Квадратная матрица А называется невырожденной, если определитель ∆ = det A ≠0. В противном случае (∆ = 0) матрица А называется вырожденной.
Союзная и обратная матрицы
Матрицей, союзной к матрице А, называется матрица
A*=  ,
,
где А  - алгебраическое дополнение элемента а
- алгебраическое дополнение элемента а  данной матрицы А. Матрица А
данной матрицы А. Матрица А 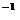 называется обратной матрице А, если выполняется условие А·А
называется обратной матрице А, если выполняется условие А·А 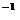 = А
= А 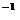 · А = Е,
· А = Е,
где Е – единичная матрица того же порядка, что и матрица А.
Пусть А – невырожденная матрица
A =  , и det A ≠0.
, и det A ≠0.
Составим союзную матрицу A *=  . Тогда A
. Тогда A 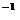 =
= 
 , т.е.
, т.е.
A 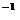 =
=  ·
· 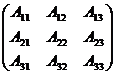 .
.
Отметим свойства обратной матрицы:
- det(A
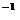 ) =
) =  ; 2. (A·B)
; 2. (A·B) 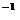 = B
= B 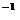 · A
· A 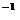 ; 3.(A
; 3.(A 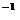 )
) 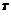 = (A
= (A 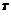 )
) 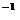 .
.
Пример 4. Найти А 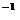 , если
, если 
Решение: 

Составим союзную матрицу. Для этого вычислим алгебраические дополнения:


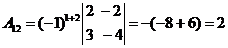
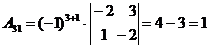





Союзная матрица будет следующей:  . Вычислим обратную матрицу:
. Вычислим обратную матрицу:


Проверкой 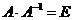 убеждаемся, что обратная матрица найдена верно.
убеждаемся, что обратная матрица найдена верно.
Задание
Даны матрицы А и В. Найти:
- A + B, A - B; 2. C =2 A -3 B; 3. AB; BA; 4. det A; det B; 5 .A ‾ ¹, B ‾ ¹. Проверить правильность их нахождения умножением
 :
:
Вариант 1: Вариант 2:
A = 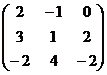 ; B =
; B =  ; A =
; A = 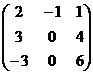 ; B =
; B =  »
»
Вариант 3: Вариант 4:
A =  ; B =
; B =  ; A =
; A =  ; B =
; B =  ;
;
4. Контрольные вопросы:
1. Что называется матрицей? Дать определения основных понятий матрицы;
2. Какая матрица называется квадратной? Единичной?
3. Какие операции можно производить над матрицами?
4. Что такое определитель матрицы? Перечислите его свойства;
5. Как вычислить минор и алгебраическое дополнение элемента  матрицы А?
матрицы А?
6. Как найти союзную и обратную матрицы для матрицы А?
5. Содержание отчёта:
5.1 Наименование работы
5.2 Цель работы
5.3 Задание
5.4 Формулы для расчета
5.5 Необходимые расчеты. Анализ результатов расчетов
5.6 Выводы по работе
5.7 Ответы на контрольные вопросы
6. Литература:
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие –
М. Новая волна, 2005, ч.1, с.99-130;
2.Подольский В. А. Сборник задач по математике: Учебное пособие - М. Высшая школа, 2005,
с.78-102;
3. Кремер Н.Ш. Высшая математика для экономистов – учебник для вузов – М.: Юнити, 2003 г,
с.9-38