Апреля Методы интегрирования Сдать 17 апреля 11Д
Апреля Методы интегрирования Сдать 21 апреля 219Д
Тема 3.1.2 Неопределенный интеграл.
Цель: - знать определение неопределенного интеграла;
- знать правила интегрирования;
-использовать знания для преобразования выражений.
Задание по уроку, выполнить в тетради:
Составить конспект по теме, записать таблицу первообразных функций
Разобрать методы интегрирования. Записать примеры и решить аналогичные.
Решить примеры на закрепление
Теоретический материал.
Определение: Функция F(х) называется первообразной функции f(х) на некотором промежутке, если для всех х из этого промежутка существует производная F'(x), равная f(x)., т.е. F'(x)= f(x).
Множество первообразных для данной функции f(x) называется неопределенным интегралом и обозначается следующим образом:  . При этом f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования, константа C – постоянной интегрирования. Здесь F(x) - первообразная от функции f(x).
. При этом f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования, константа C – постоянной интегрирования. Здесь F(x) - первообразная от функции f(x).
Например:  .
.
Операция нахождения неопределенного интеграла называется интегрированием функции. Интегрирование есть действие, обратное дифференцированию.
Правила интегрирования:
1.Для получения неопределенного интеграла от данной функции f(x) необходимо найти одну из ее первообразных и прибавить к ней произвольную постоянную.
2.Для проверки правильности полученного результата необходимо помнить, что производная от результата интегрирования должна равняться подынтегральной функции.
Тема 3.1.3 Основные свойства неопределенного интеграла.
Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению.
Свойтсво2. Неопределенный интеграл от производной (дифференциала) функции равен этой функции, сложенной с произвольной постоянной.
Свойство3. Если две функции или два дифференциала тождественны, то неопределенные интегралы от них могут отличаться только на постоянное слагаемое.
Свойство4. Постоянный множитель можно выносить за знак интеграла:
 где а = const, a≠0.
где а = const, a≠0.
Пример. Найти 
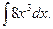 Решение.
Решение. 
Свойство5. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:


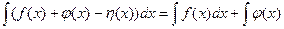 dx -
dx - 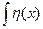 dx.
dx.
Для нас важны 4 и 5 свойства. Используя эти правила будем находить первообразную функцию
Тема 3.1.4 Основные формулы интегрирования.
Переменная обозначена z, формулы такие же с переменной х.
Таблица интегралов:
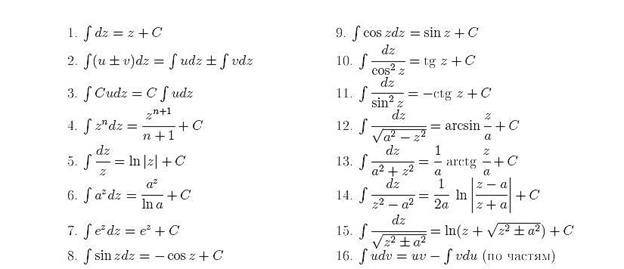
Тема 3.1.5 Методы интегрирования
I. Непосредственное интегрирование.
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример1. Найти 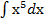 . Решение: Используем формулу 4 из таблицы интегралов, т.е.
. Решение: Используем формулу 4 из таблицы интегралов, т.е.
 dx=
dx=  +C. Сами:
+C. Сами:  =
=
Для проверки результата находим производную от ответа.
Пример2. Найти 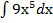 . Решение: Используем формулы 3,4 из таблицы интегралов, т.е.выносим числовой множитель за знак интеграла и затем находим первообразную:
. Решение: Используем формулы 3,4 из таблицы интегралов, т.е.выносим числовой множитель за знак интеграла и затем находим первообразную:
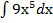 = 9
= 9 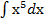 =9.
=9.  +C=
+C=  +С. Сами:
+С. Сами:  =
=
Пример3. Найти 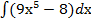 . Решение: Используем формулы 1,2,3,4 из таблицы интегралов,, т.е. находим интеграл суммы, выносим числовой множитель за знак интеграла и затем находим первообразную:
. Решение: Используем формулы 1,2,3,4 из таблицы интегралов,, т.е. находим интеграл суммы, выносим числовой множитель за знак интеграла и затем находим первообразную:
 = 9
= 9  -8.
-8.  =9.
=9. 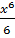 - 8x+C=
- 8x+C= 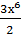 -8x +С.
-8x +С.
Сами: 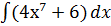 =
=
Пример 4. Найти  .
.
Решение:  =
= 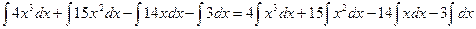 =
=
=  =
= 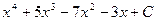 .
.
Сами:  +3
+3 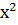 -6х -5)
-6х -5)  .
.
Для вычисления интегралов часто приходится представлять выражение в виде удобном для их вычисления с помощью таблицы и свойств. В этом примере показано, как это делать.
Пример 5. Найти 
Решение: 
=  Сами:
Сами: 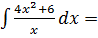
Вы сейчас на примерах разобрали, как выполнить интегрирование методом «непосредственного интегрирования». Закрепите на примерах.
1) 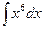
| |
2) 
| |
3) 
| |
4) 
| Сначала упрощаем: корень заменяем степенью и затем сокращаем, т.е основание оставляем тем же, а показатели вычитаем и используем формулу 4. Числовой множитель  выносим за знак интеграла выносим за знак интеграла
|
5) 
|
II.Метод подстановки.
Этот метод называют также методом замены переменной. Он является одним из наиболее эффективных и распространенных приемов интегрирования, позволяющих во многих случаях упростить вычисление интеграла. Теория сложная, постаралась объяснить на примерах. Теорию прочитайте и записывайте примеры.
Предположим, что на промежутке [a,b]  и, допустим, что функция
и, допустим, что функция  непрерывна вместе со своей первой производной в промежутке
непрерывна вместе со своей первой производной в промежутке  для всех точек t промежутка
для всех точек t промежутка 
При этих предположениях сложная функция F( 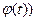 определена при
определена при  и
и
 Так как
Так как  то
то
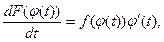 откуда
откуда 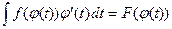
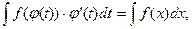 где
где 
После интегрирования возвращаются к старой переменной, используя обратную подстановку 
Подстановку  необходимо выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства.
необходимо выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства.
Общих правил для нахождения нужной подстановки нет. Рассмотрим частные случаи.
Если подынтегральная функция имеет вид f(ax+b), то можно использовать подстановку ax+b=t.
Пример1. Найти  .
.
Решение: Сразу табличные интегралы использовать нельзя, т.к. (4х-5)5 сложная функция. Решаем способом подстановки. Пусть (4х-5)=t, найдем дифференциал от 4х-5. Вы помните, что дифференциал – это производная функции, т.е. d(4x-5)=4dx, значит dt = d(4x-5)=4dx. Отсюда получаем: dx =  .Запишем интеграл в новом виде и найдем его:
.Запишем интеграл в новом виде и найдем его:
 =
= 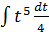 =
= 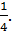
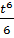 +C=
+C= 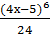 +С.
+С.
Пример2. Найти 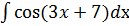 . Решение: используем метод подстановки.
. Решение: используем метод подстановки. 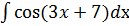 = [3x+7=t, dt=3dx, dx=
= [3x+7=t, dt=3dx, dx= 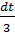 ] =
] =  =
=  =
=  sin(3x+7).
sin(3x+7).
Пример3. Найти 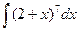 .
.
Решение. Введем новую переменную 2+x=t; 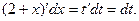 Найдем интеграл:
Найдем интеграл: 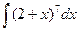 =
= 
Выразим результат через первоначальный аргумент:
 =
= 
Пример4. Найти  .
.
Решение. Используя формулы интегрирования, получаем:

Вы сейчас на примерах разобрали, как выполнить интегрирование методом подстановки. Закрепите на примерах.
1) 
| 5) 
|
2) 
| 6) 
|
3) 
| 7) 
|
4) 
| 8) 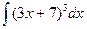
|
Задание по уроку: 1. Составить конспект по теме, записать таблицу первообразных функций 2.Разобрать методы интегрирования. Записать примеры и решить аналогичные. 3.Решить примеры на закрепление