1. 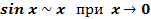 ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 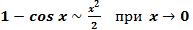 ;
;
6.  ;
;
7.  ;
;
8.  .
.
Пример: Вычислить пределы:
1. 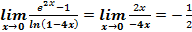 ;
;
2.  ;
;
3.  .
.
Упражнения: Вычислить пределы:
1. 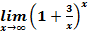 ;
;
2. 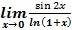 ;
;
3.  ;
;
4. 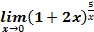 ;
;
5.  ;
;
6.  .
.
8. Точки разрыва функции и их классификация
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х = х0 – точка разрыва функции 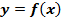 , то в ней не выполняется хотя бы одно из условий определения непрерывности функции:
, то в ней не выполняется хотя бы одно из условий определения непрерывности функции:
1) функция определена в точке х0;
2) существует конечный предел функции в точке х0;
3) предел функции в точке х0 равен значению функции в этой точке, то есть  .
.
Пример:
1. Функция определена в окрестности точки х0, но не определена в самой точке х0:  , х0= 2 –точка разрыва.
, х0= 2 –точка разрыва.
2. Функция определена в точке х0 и её окрестности, но не существует предела функции при х→х0: 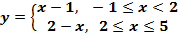 , х0= 2 – точка разрыва.
, х0= 2 – точка разрыва.
3. Функция определена в точке х0 и её окрестности, существует предел функции при х→ х0, но этот предел не равен значению функции в точке х0 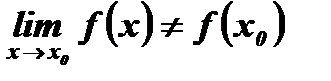 :
:  , х0= 0 – точка разрыва.
, х0= 0 – точка разрыва.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение: Точка разрыва х0 называется точкой разрыва первого рода функции 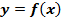 , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е. 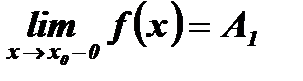 и
и 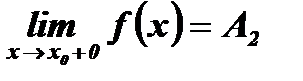 , при этом:
, при этом:
а) если  , то точка х0 называется точкой устранимого разрыва;
, то точка х0 называется точкой устранимого разрыва;
б) если 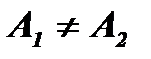 , то точка х0 называется точкой конечного разрыва.
, то точка х0 называется точкой конечного разрыва.
Величину  называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
Определение: Точка разрыва х0 называется точкой разрыва второго рода функции 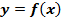 , если в этой точке по крайней мере один из односторонних пределов не существует или равен бесконечности.
, если в этой точке по крайней мере один из односторонних пределов не существует или равен бесконечности.
1.  , х0= 2 – точка разрыва второго рода.
, х0= 2 – точка разрыва второго рода.
2. 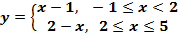 , х0= 2 – точка разрыва первого рода, скачок функции равен 1.
, х0= 2 – точка разрыва первого рода, скачок функции равен 1.
3.  , х0= 0 – точка устранимого разрыва первого рода. Положив у = 1 (вместо у = 2) при х = 0, мы устраним разрыв, функция станет непрерывной.
, х0= 0 – точка устранимого разрыва первого рода. Положив у = 1 (вместо у = 2) при х = 0, мы устраним разрыв, функция станет непрерывной.
Пример: Найти точки разрыва функции  и определить их тип.
и определить их тип.
Решение: Функция определена и непрерывна на всей числовой оси, кроме точки х = 3. Очевидно, что  . Следовательно,
. Следовательно,  , а
, а  . Поэтому в точке х = 3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 2.
. Поэтому в точке х = 3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 2.
Упражнения:
1. Найти точки разрыва функции 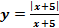 и определить их тип.
и определить их тип.
2. Найти точки разрыва функции  и определить их тип.
и определить их тип.
9. Асимптоты графика функции.
Определение: Асимптотой графика функции называется прямая, расстояние до которой от точки, лежащей на графике, стремится к нулю при неограниченном удалении от начала координат этой точки по графику функции.
Вывод: Асимптоты могут быть вертикальными, горизонтальными, наклонными.
Пример:
1. Функция 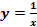 имеет вертикальную асимптоту х = 0, горизонтальную асимптоту у = 0.
имеет вертикальную асимптоту х = 0, горизонтальную асимптоту у = 0.
2. Функция 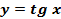 имеет вертикальные асимптоты
имеет вертикальные асимптоты 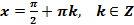 .
.
Вывод:
1. Прямая х = а является вертикальной асимптотой графика функции 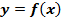 , если
, если  , или
, или  , или
, или  .
.
2. Для отыскания вертикальных асимптот графика функции 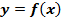 нужно найти те значения аргумента х, вблизи которых функция
нужно найти те значения аргумента х, вблизи которых функция 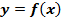 неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
3. Если существует наклонная асимптота, то её уравнение имеет вид  , где
, где  ,
,  . Если хотя бы один из этих пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.
. Если хотя бы один из этих пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.
4. Если 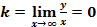 , то
, то 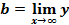 . Прямая
. Прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 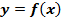 .
.
Замечание: Асимптоты графика функции 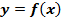 при
при  ипри
ипри  могут быть разными. Поэтому при нахождении пределов
могут быть разными. Поэтому при нахождении пределов  и
и  следует отдельно рассматривать случай, когда
следует отдельно рассматривать случай, когда  икогда
икогда  .
.
Пример: Найти асимптоты графика функции  .
.
 - график не имеет наклонной асимптоты при
- график не имеет наклонной асимптоты при  .
.

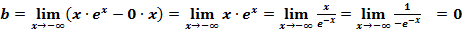
При  график имеет горизонтальную асимптоту у = 0.
график имеет горизонтальную асимптоту у = 0.
Упражнения:
Найти асимптоты графика функции:
1. 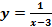
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
|
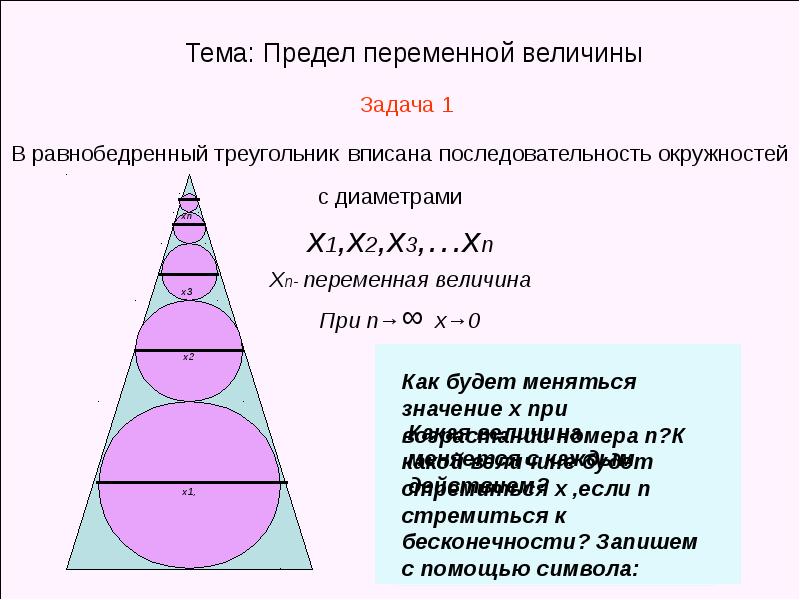
Обобщённое понятие предела:
Число А есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к числу А.
Примеры:
Скорость машины на трассе