ОТЧЕТ
Дисциплина: Методы оптимизации
Тема: Градиентные методы
Выполнил студент гр. 33601/1 Д.О. Труфанов
Руководитель, доцент Е.А. Родионова
«___»________________2015 г.
Санкт-Петербург
В данной работе исследуются градиентные методы первого порядка: метод наискорейшего спуска, метод с постоянным шагом; градиентный метод второго порядкас дроблением шага; метод Флетчера-Ривса.
Постановка задачи
Найти минимум функции двух переменных

Найти минимум функции пяти переменных

методом Флетчера-Ривса.
Вычисления произвести с точностью 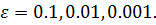 В методе наискорейшего спуска показать независимость от выбора начального приближения и ортогональность звеньев градиентной ломаной. Провести сравнительный анализ скорости сходимости метода с постоянным шагом и метода наискорейшего спуска. Подтвердить, что для квадратичной формы метод Флетчера-Ривса сходятся не более, чем за 5 шагов. Показать квадратичную скорость сходимости метода Флетчера-Ривса.
В методе наискорейшего спуска показать независимость от выбора начального приближения и ортогональность звеньев градиентной ломаной. Провести сравнительный анализ скорости сходимости метода с постоянным шагом и метода наискорейшего спуска. Подтвердить, что для квадратичной формы метод Флетчера-Ривса сходятся не более, чем за 5 шагов. Показать квадратичную скорость сходимости метода Флетчера-Ривса.
Условия применимости метода
Для функции двух переменных найдем соответствующую матрицу Гессе.
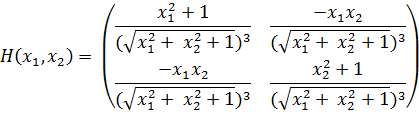
Найдем собственные числа матрицы Гессе. Это будут
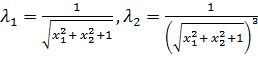 .
.
Нетрудно видеть, что 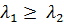 .
.
Допустим, что решение задачи ищется в круге  .Тогда заметим, что
.Тогда заметим, что  . Таким образом, получены оценки на собственные числа матрицы Гессе
. Таким образом, получены оценки на собственные числа матрицы Гессе 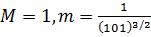 в данной области. Так как, это оценки собственных чисел матрицы Гессе, то можно заключить, что
в данной области. Так как, это оценки собственных чисел матрицы Гессе, то можно заключить, что
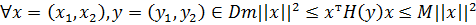 .
.
Также введенная функция  является строго выпуклой, поскольку, как можно заметить, ее матрица Гессе является положительно определенной по критерию Сильвестра.
является строго выпуклой, поскольку, как можно заметить, ее матрица Гессе является положительно определенной по критерию Сильвестра.
Таким образом, выполнены необходимые условия теорем о сходимости соответствующих градиентных методов независимо от начального приближения, следовательно, данные градиентные методы применимы к данной задаче в данной области.
Кроме этого, метод Флетчера-Ривса для данных функции также применимы, поскольку матрица Гессе для функции двух переменных и матрица квадратичной формы от пяти переменных – симметричные и положительно определенные по критерию Сильвестра.
Описание алгоритма
1. Метод наискорейшего спуска.
Зададимся начальным приближением 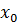 искомого минимума функции
искомого минимума функции  в заданной области. На каждом шаге метода в качестве направления спуска выбираем антиградиент минимизируемой функции в текущей точке
в заданной области. На каждом шаге метода в качестве направления спуска выбираем антиградиент минимизируемой функции в текущей точке 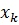 . Для нахождения величины шага вдоль заданного направления решается задача одномерной минимизации
. Для нахождения величины шага вдоль заданного направления решается задача одномерной минимизации  при
при 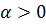 , решение которой и выбирается в качестве величины шага. Решение считается полученным с заданной точностью при выполнении неравенства
, решение которой и выбирается в качестве величины шага. Решение считается полученным с заданной точностью при выполнении неравенства  .
.
2. Метод с постоянным шагом.
Пусть 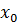 - начальное приближение минимума функции
- начальное приближение минимума функции  в заданной области. На каждом шаге метода в качестве направления спуска выбираем антиградиент минимизируемой функции в текущей точке
в заданной области. На каждом шаге метода в качестве направления спуска выбираем антиградиент минимизируемой функции в текущей точке 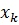 . В качестве шага выбирается постоянная величина
. В качестве шага выбирается постоянная величина 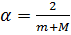 , которая из теоретических соображений дает сходимость метода, притом наилучшую. Для проверки оптимальности текущего решения используется следующее условие:
, которая из теоретических соображений дает сходимость метода, притом наилучшую. Для проверки оптимальности текущего решения используется следующее условие:  .
.
3. Метод второго порядка с дроблением шага.
Зададимся начальным приближением искомого минимума функции  , равным
, равным 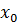 . На каждом шаге метода в качестве направление выбираем величину
. На каждом шаге метода в качестве направление выбираем величину 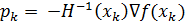 , где
, где 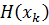 - матрица Гессе минимизируемой функции в данной точке. Для нахождения шага построим следующую процедуру. Пусть
- матрица Гессе минимизируемой функции в данной точке. Для нахождения шага построим следующую процедуру. Пусть 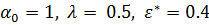 . Для текущего
. Для текущего 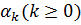 проверяем следующее неравенство:
проверяем следующее неравенство: 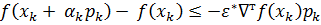 . Если оно не выполняется, то рассчитываем
. Если оно не выполняется, то рассчитываем 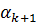 по формуле
по формуле 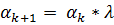 . Если данное неравенство выполняется, что в качестве шага в заданном направлении принимается
. Если данное неравенство выполняется, что в качестве шага в заданном направлении принимается 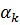 .Решение считается полученным с заданной точностью, когда выполняется неравенство
.Решение считается полученным с заданной точностью, когда выполняется неравенство  .
.
4. Метод Флетчера-Ривса.
Пусть  - матрица Гессе минимизируемой функции,
- матрица Гессе минимизируемой функции, 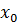 - начальное приближение искомого решения.
- начальное приближение искомого решения.
Пусть  . Тогда для в случае, когда минимизируется значениеквадратичной формы,
. Тогда для в случае, когда минимизируется значениеквадратичной формы, 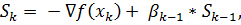 где
где 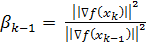 , а в противном случае
, а в противном случае 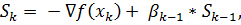 где
где 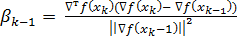 ,если
,если 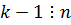 , где
, где  - размерность пространства, и 0 в противном случае.
- размерность пространства, и 0 в противном случае.
На 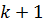 -ом шаге метода в качестве направления выбирается
-ом шаге метода в качестве направления выбирается 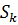 , а в качестве величины шага - решение задачи одномерной минимизации
, а в качестве величины шага - решение задачи одномерной минимизации 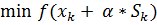 при
при 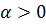 . Для проверки оптимальности текущего решения используется условие на норму градиента минимизируемой функции в текущей точке:
. Для проверки оптимальности текущего решения используется условие на норму градиента минимизируемой функции в текущей точке:  .
.
Полученные результаты
Аналитическим решением задачи минимизации функции двух переменных будет точка 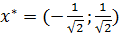 , а квадратичная форма от пяти переменных достигает минимума в точке
, а квадратичная форма от пяти переменных достигает минимума в точке  , где
, где 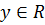 .
.
В качестве начального приближения использовались  .
.
Для каждого метода укажем количество шагов, необходимое для нахождения решения.
1) 
Метод наискорейшего спуска – 3 шагов.
Метод с постоянным шагом – 8 шагов.
Метод второго порядка с дроблением шага – 9 шага.
Метод Флетчера-Ривса (для функции двух переменных) – 7 шагов.
Метод Флетчера-Ривса (для квадратичной формы) – 2 шага.
2) 
Метод наискорейшего спуска –5 шагов.
Метод с постоянным шагом –10 шагов.
Метод второго порядка с дроблением шага –15шагов.
Метод Флетчера-Ривса (для функции двух переменных) – 8 шагов.
Метод Флетчера-Ривса (для квадратичной формы) – 4 шага.
2) 
Метод наискорейшего спуска – 6 шагов.
Метод с постоянным шагом – 11 шагов.
Метод второго порядка с дроблением шага – 22 шагов.
Метод Флетчера-Ривса (для функции двух переменных) – 10 шагов.
Метод Флетчера-Ривса (для квадратичной формы) – 5 шага.
Проверка полученных теоретических оценок для метода наискорейшего спуска (
1) 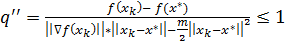
Полученные значения
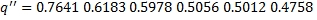 .
.
2) 
Полученные значения
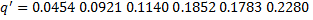 .
.
3) 
Полученные значения
 .
.
4) Проверка ортогональности звеньев градиентной ломаной
Полученные значения для косинуса угла между векторами:
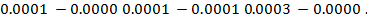
Обоснование достоверности полученных результатов
Достоверность полученных результатов объясняется численным подтверждением следующих теоретических результатов:
1) Градиентные методы первого порядка имеют линейную скорость сходимости, остальные – квадратичную (или близкую к ней).
2) Метод Флетчера-Ривса сходится не более, чем за 5 шагов для квадратичной формы.
3) Звенья градиентной ломаной ортогональны в методе наискорейшего спуска.
4) Выполнены теоретические оценки для метода наискорейшего спуска, связанные с параметром 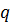 сходимости метода, а также с разностью между значением функции на текущем шаге и точным решением.
сходимости метода, а также с разностью между значением функции на текущем шаге и точным решением.