Преобразование координат

Кривые второго порядка

 

Будем рассматривать множества L точек евклидовой плоскости

Другое название для L - геометрическое место точек(ГМТ) в .

Будем считать, что на плоскости введена некоторая декартова прямоугольная система координат ХОУ

 

 

 

 

Координаты точки М принадлежащей плоскости , будем обозначать через х и у.

 

Определение. Уравнение данного ГМТ – это необходимое и достаточное условие принадлежности точки М(x,y) данному ГМТ, выраженное в форме уравнения или системы уравнений, роль неизвестной в котором или в которой играет сама точка или ее координаты в некоторой координатной системе.

 

Определение. Геометрическое место L точек(ГМТ) плоскости уравнение которого имеет вид

(1)

Пусть далее константы (вещественные числа).

В уравнении (1) по крайней мере один из коэффициентов при старших членах отличен от нуля.()

 

Иначе говоря кривая второго порядка - это такое ГМТ левая часть уравнения которого является полиномом второй сткепени от координат x y.

,

 

Три замечательных кривых

Гипербола

Определение. Гиперболой (Г) называется ГМТ плоскости, абсолютная величина разности расстояний от каждой из которых до двух фиксированных точек этой плоскости (называемых фокусами) есть величина постоянная, она меньше расстояний между фокусами.

 

 

 

Осью гиперболы называется прямая, соединяющая её фокусы.

Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы .

Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы .

Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы .

Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом: . Эксцентриситет гиперболы всегда больше единицы.

Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром ..

M(x, y) – точка на гиперболе, F₁, F₂ – фокусы гиперболы.

r_1, r₂ – расстояния от точки М до фокусов.

По определению ïr₁ – r₂ï= 2a. F₁F₂ = 2c. Выберем на гиперболе произвольную точку М(х, у).

Тогда:

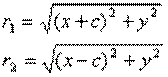
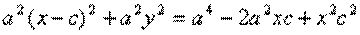
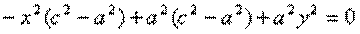
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось) =>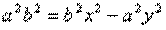

Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

<= Сопряженная гипербола

 

Эллипс

Определение. Э ллипс (Э) - ГМТ в плоскости {Э}, сумма расстояний от каждой из которых до двух фиксированных точек F₁ и F₂ плоскости, называемых фокусами есть величина постоянная равная

Выводится каноническое уравнение эллипса аналогично каноническому уравнению гиперболы.

 

На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ox примем прямую, проходящую через фокусы F₁ и F₂, а за ось Oy – прямую, перпендикулярную к F₁F₂ и проведённую через середину отрезка F₁F₂ (рис. 2). Обозначим расстояние F₁F₂ между фокусами через 2с, тогда координаты фокусов будут: F₂ (с;0) и F₁(-с;0).

Возьмем на эллипсе произвольную точку M (x,y). Обозначим постоянную величину суммы расстояний от каждой точки до фокусов через 2а, тогда F₁M+ F₂M=2a (2)

 

По формуле расстояний между двумя точками найдём F₁M и F₂M.

Упростим выражения и получим:

, где

Это и будет каноническим уравнением эллипса.

 

При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Число

где а - большая полуось, называется эксцентриситетом эллипса. Очевидно, (для окружности ). Если М(x;y) - произвольная точка эллипса, то отрезки и (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам

, .

Если эллипс определен уравнением (1) и , то прямые

,

(рис.) называются директрисами эллипса (если , то директрисы определяются уравнениями , .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r к d (r/d) есть постоянная величина, равная эксцентриситету эллипса:

 

 

Пользуясь определением эллипса, его легко построить непрерывным движением карандаша. Для этого берём нерастяжимую нить длиной, равной большой оси эллипса, т.е. длиной 2а, и закрепляем концы этой нити в фокусах, положение которых предполагается известным.

Натягиваем нить карандашом и остриём его описываем кривую, держа нить всё время в натянутом состоянии. Кривая, описываемая при этом – эллипс, так как сумма расстояний от любой точки этой кривой до фокусов равна длине нити, т.е. равна постоянной величине.

Парабола

 

Определение. Параболой называется ГМТ плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора . Ось Oy проведем перпендикулярно оси

 

 

Пусть расстояние между фокусом и директрисой 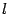параболы равно p. Тогда в выбранной системе координат парабола имеет уравнение (*)

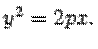
Доказательство. В выбранной системе координат фокусом параболы служит точка , а директриса имеет уравнение

Пусть - текущая точка параболы. Тогда по формуле для плоского случая находим

Расстоянием от точки 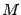до директрисы служит длина перпендикуляра , опущенного на директрису из точки . Из рисунка очевидно, что . Тогда по определению параболы , то есть

Возведем обе части последнего уравнения в квадрат:

откуда

После приведения подобных членов получим уравнение (*).

Уравнение (*) называется каноническим уравнением параболы.

Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .

Доказательство. Проводится так же, как и предыдущее доказательство

Точка пересечения оси симметрии с параболой называется вершиной параболы.

Если переобозначить переменные , , то уравнение (*) можно записать в виде

который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований

 

Уравнение директрисы : , фокус — , таким образом начало координат 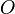— середина отрезка . По определению параболы для любой точки 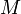, лежащей на ней выполняется равенство . и , тогда равенство приобретает вид:

.

После возведения в квадрат и некоторых преобразований получается равносильное уравнение .

Парабола — кривая второго порядка.

Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.

Пучок лучей параллельных оси, отражаясь в параболе собирается в её фокусе. Для параболы фокус находится в точке (0,25; 0).

Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

 

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые ()
Эллипс
Гипербола
Парабола
Вырожденные кривые (Δ = 0)
Точка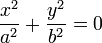
Две пересекающиеся прямые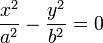
Две параллельные прямые
Одна прямая	x 2 = 0

Конические сечения

Функции двух переменных

 

 

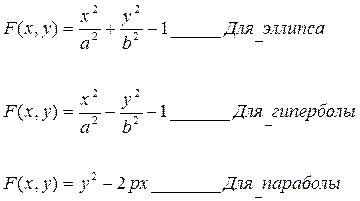
Преобразование координат

Параллельный перенос:

Пусть на плоскости заданы две декартовы прямоугольные системы координат: 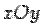("старая") и ("новая"), причем как оси абсцисс, так и оси ординат обеих систем параллельны и одинаково направлены

 

<=Параллельный перенос системы координат

 

В этом случае говорят, что одна система координат получается из другой "параллельным переносом".

Пусть начало "новой" системы координат имеет в "старой" системе координат координаты 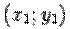, и пусть 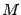- некоторая точка плоскости. Обозначим координаты точки 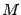в "старой" системе координат 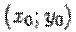, а в "новой" - 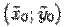. Из рисунка ясно, что , .

Откуда , 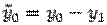. Так как точка взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:

(1)

Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.

Пусть некоторая кривая задана уравнением . Тогда в системе координат , полученной параллельным переносом, с началом в точке 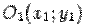уравнение кривой будет иметь вид .

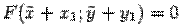Однако, для практического использования это предложение удобнее сформулировать немного по-другому.

Пусть некоторая кривая задана уравнением 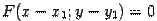. Тогда в системе координат 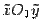, полученной параллельным переносом, с началом в точке уравнение кривой будет иметь вид .

Доказательство обоих предложений очевидным образом следует из формул (1) связи между старыми и новыми координатами.

Поворот:

Выведем формулу преобразования координат при повороте координатных осей.

Повернём оси координат на угол α относительно

исходной системы координат. Координаты точки М

в системе координат x′Oy′ равны x′ и y′. Найдём её

координаты в системе коорднат xOy. В треугольнике

CMD ∠CMD = α, OD=x′, MD=y′.

Следовательно, x=OA=OB-AB=OB-CD,

y=MA=AC-CM=DB+CM.

Поскольку

OB = x′ cos α, CD = y′ sin α,

CM = y′ cos α, DB = x′ sin α,

x = x′ cos α − y′ sin α,

то

y = x′ sin α + y′ cos α.

Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x′,y′) этой же точки при повороте осей на угол α.

Формулы, выражающие новые координаты (x′,y′) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол α, то старая система получается поворотом

новой на угол (-α), поэтому в равенствах можно поменять местами старые и новые координаты, заменяя одновременно α на (-α).

Выполнив это преобразование, получим

x′ = x cos α + y sin α,

y′ = − x sin α + y cos α.

При этом, например, уравнения директрис эллипса (гиперболы) и параболы принимают вид:

x′ cos α − y′ sin α = ± ;

x′ cos α − y′ sin α = − .