Дифференциальные уравнения высшего порядка

Лабораторная работа N2.

Моделирование динамических систем. Решение систем дифференциальных уравнений.

Цель работы:

Разработка алгоритмов и программ моделирования систем дифференци­альных уравнений методами:

1. Эйлера-Коши;

2. Эйлера-Коши c итерациями;

3. модифицированным методом Эйлера;

4. методом трапеций;

5. методом Рунге-Кутта 4_го порядка;

6. методом Рунге-Кутта с автоматическим изменением шага;

7. методом Рунге-Кутта-Мерсона с автоматическим изменением шага;

8. методом Рунге-Кутта-Фельберга с автоматическим изменением шага;

Порядок выполнения работы:

I. Разработать программную реализацию для приведенных методов решения систем дифференциальных уравнений.

2. Получить решения для заданных систем дифференциальных уравнений в соответствии с индивидуальными заданиями.

3. Представить графические результаты вычислений.

Отчет о работе должен содержать:

1. Содержание

2. Описание методов решения систем дифференциальных уравнений;

3. Блок-схема алгоритма решения поставленной задачи.

4. Листинг программы (с комментариями).

5. Скриншоты программы с графиками процессов.

6. Выводы

 

 

Требования к оформлению:

Размер лабораторной работы - около 10 стр. Выводы должны занимать не больше 1 стр;

Стандартный шрифт Times New Roman (14 пт.) с межстрочным единичным интервалом и отступом «первой строки» — 1,25 см;

Методические указания:

Задача Коши заключается в решений систем обыкновенных дифференциальных уравнений первого порядка, представляемых в виде

dy₁/dx = F₁ (x,y₁,...,y_J,...,y_N),

dy_j/dx= F_J(x,y₁,...,y_J,...,y_N), (1)

dy_n/dx= F_N(x,y₁,...,y_J,...,y_N),

где j=1-N- номер каждой зависимой переменной у_j,х- независимая переменная. Если задача Коши решается для анализа поведения системы или объекта во времени, то х является временем (x=t). Решение системы (I) при заданных начальных условиях х=х₀, у₁(x₀)=y₁₀, y₂(x₀)=y₂₀,…,y_N(x₀)=y_N0 сводится к наложению зависимостей (интегральных кривых) y₁(x),y₂(x),…,y_N(х), проходящих через точки, заданные начальными условиями (x₀,y₁₀),(х₀,y₂₀),...,(x₀,y_j0),…,(x₀,y_N0). Задача Коши сводится к интегрирований дифференциальных уравнений. Порядок метода численного интегрирования при этом определяет и порядок метода решения (I).

Обобщенная форма записи каждого из уравнений системы (1) может быть представлена в общем виде

 

dy_j /dx=F_j(x,y), (2)

 

где y_j где в правой части уравнения - векторы переменных у₁,y₂,y_j,…,y_N, а F_j- правая часть каждого из уравнений (I). В частности, одно дифференциальное уравнение (y=Y_j=Y₁ и F_j=F=F₁) записывается в виде

dy/dx=F₁(x,y).

Дифференциальные уравнения высшего порядка

y⁽ⁿ⁾=F(x,y,y^’,y^’’,…y^(n-1)), 3)

где (n) -порядок уравнения, могут быть сведены к системам вида (I) или (2) с помощью следующих преобразований:

dy/dx=y₁,

dy₁/dx=y₂, (4)

dy_n-2/dx=y_n-1,

dy_n-1/dx=F(x,y₁,y₂,…,y_n-1),

Следовательно решение (з) сводится к решению системы обыкновенных дифференциальных уравнений первого порядка (4).

1. Метод Эйлера-Коши- простейший метод первого порядка для численного интегрирования дифференциальных уравнений. Он реализуется следующей рекурентной формулой:

y_j(i+1)=y_ji+hF_j(x_i,y_ji).

где h- шаг интегрирования (приращение переменной x). Этот метод обладает большой погрешностью и имеет систематическое накопление ошибок. Погрешность метода R ~ (h²), т.е. пропорциональна h².

2. Метод Эйлера-Коши с итерациями заключается в вычислении на каждом шаге начального значения

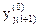= Y_ji + hF_j (x_i,Y_ji).

Затем с помощью итерационной формулы

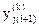=y_ji+h/2 [ F_j(x_i,y_ji)+F_j(x_i+1, ) ]

решение уточняется. Итерации проводят до тех пор, пока не совпадет заданное число цифр результата на двух последних шагах итераций. Погрешность метода R~ (h²). Обычно число итераций не должно пре­вышать 3-4, иначе нужно уменьшить шаг h.

3. Модифицированный метод Эйлера второго порядка реализуется следующими рекурентными формулами:

Y_j(i+1)=y_ji+hF_j(x_i+h/2,y^*_j(i+1/2)),

где y^*_j(i+1/2)=y_ji+hF_j(x_i,y_ji)/2

Метод дает погрешность R ~ (h²) и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения.

4. Метод трапеций - одна из модификаций метода Эйлера второго порядка. Он реализуется применением на каждом шаге формулы

y_j(i+1)=y_ji+1/2(K_j1+K_j2),

где K_j1 =hF_j (x_i,y_ji), K_j2=hF_J (x_i+h, y_ji+K_j1), и дает погрешность

R ~ (h²). Этот метод относится к общим методам Рунге-Кутта. Не рекомендуется при сильной крутизне, т.к. возможно возникновение численной неустойчивости (уменьшить шаг).

5. Метод Рунге-Кутта четвертого порядка является наиболее

распространенным методом решения систем (2) при шаге h=const. Его достоинством является высокая точность - погрешность R ~ (h⁵) - и меньшая склонность к возникновению неустойчивости решения. Алгоритм реализации метода Рунге-Кутта заключается в циклических вычислениях y_j(i+1) на каждом шаге i+1 шаге по следующим формулам:

K_1j=hF_j(x_i,y_ji),

K_2j=hF_j(x_i+h/2, y_ji+ 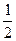K_1j)

K_3j=hF_j(x_i+h/2, y_ji+ 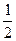K_2j)

K_4j=hF_j(x_i+h, y_ji+K_3j)

Y_j(i+1)=y_ji+1/6(K_1j+2K_2j+2K_3j+K_4j)

При переходе от одной формулы к другой задаются или вычисляются соответствующие значения х и Y_j. и находятся по подпрограмме значения функций F_j(x,y_j).

Решение одного дифференциального уравнения методом Рунге-Кутта производится по приведенным формулам, если в них опустить индекс j, а из алгоритма исключить циклы. Последнее резко упрощает программу и позволяет получить минимально возможное время счета.

Ввиду особого значения и широкого применения дифференциальных уравнений второго порядка полезно иметь специальную программу для их решения.

Метод Рунге-Кутта для дифференциального уравнения второго порядка вида

Y^''= =F(x,y,y')

имеющий погрешность R ~ (h⁵), реализуется с помощью следующих формул:

К₁ = hF(x_i;y_i;y'_i);

K₂=hF(x_i+h/2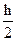; y_i+ y'_i+ 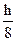K₁; y'_i+K₁/2);

K₃=hF(x_i+h/2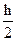; y_i+ y'_i+ 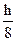K₁; y'_i+K₂/2);

K₄=hF(x_i+h; y_i+hy'_i+ 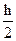K₃; y'_i+K₃);

Y^'_i+1=y'_i+1/6(K₁+2K₂+2K₃+K₄)

Перед началом вычислений надо задать шаг h и начальные значения х x₀, y(x₀)=y₀ и y^'(x₀)=y^'₀.

Автоматическое изменение шага в ходе решения систем

дифференциальных уравнений необходимо, если решение требуется получить с заданной точностью. При высокой точности (погрешность e=Е=1*10^-9) и решении в виде кривых с сильно различающейся крутизной автоматическое изменение шага обеспечивает уменьшение общего числа шагов в несколько раз, резко уменьшает вероятность возникновения числовой неустойчивости, дает более равномерное расположение точек графика кривых (решений) при их выводе на печать.

6. Метод Рунге-Кутта с автоматическим изменением шага заключается в том, что после вычисления _Yj(i+1) c шагом h все вычисления проводятся повторно с шагом h/2. Полученный результат 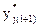сравни­вается с y_j(i+1). Если |y_j(i+1) - y^*_j(i+1)|<e, вычисления продолжа­ется с шагом h, в противном случае шаг уменьшают. Если это неравенство слишком сильное, шаг, напротив, увеличивают. При той же погрешности R ~ (h⁵) лучшие результаты дает описанный ниже метод.