Методы корреляционного и регрессионного анализа

1.1. Понятие корреляции

Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями и процессами. Для того, чтобы объективно и основательно проникнуть в суть изучаемого явления или процесса, необходимо изучить его связь с другими явлениями или процессами. При таком изучении основное внимание, как правило, уделяется причинному объяснению связей.

Под причинной связью понимается такое соединение явлений и процессов, когда изменение одного из них происходит вследствие изменения другого. Связи между явлениями могут быть различны по силе. При изменении степени, интенсивности, тесноты, прямолинейности, четкости, строгости связи проблема корреляции рассматривается в узком смысле. Исходя из этого, можно сделать определение: если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляционная связь, или корреляция. О функциональной связи говорят в том случае, когда все переменные в причинной связи детерминированы, и, как следствие, предполагается не вероятностная, а детерминированная связь.

Функциональная и корреляционная связь – два основных типа связи, определяющих соотношение между явлениями и процессами. Следует отметить, что иногда истинную функциональную связь трудно обнаружить из-за накладывающихся погрешностей измерения, изменения условий реализации, ошибочного или формально рассмотрения причинных отношений. [11]

1.2. Виды корреляции

Относительно характера корреляции:

А) Положительная корреляция;

Б) Отрицательная корреляция.

Относительно числа переменных:

А) Простая (парная);

Б) Множественная;

В) Частная.

Относительно формы связи:

А) Линейная;

Б) Нелинейная.

Относительно типа соединения:

А) Непосредственная;

Б) Косвенная;

В) Ложная. [11]

1.3. Задачи корреляционного анализа

А) Измерение степени связности двух и более явлений.

Общие знания об объективно существующих причинных связях должны дополняться научно обоснованными знаниями о мере зависимости между явлениями. Для этого выполняются соответствующие статистические вычисления. Здесь, как правило, речь идет о верификации уже известных связей. Впрочем, корреляционный анализ так же может служить инструментом для обнаружения еще неизвестных связей.

Б) Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями.

Отобранные факторы используют для дальнейшего анализа. Самые важные факторы в рамках корреляционного анализа те, которые коррелируют сильнее всего с явлениями, подлежащими исследованию. Осознанно изменяя влияющие факторы можно достигнуть желаемого эффекта в результативном признаке-следствии. Кроме того, на основе полученных связей можно с достаточной точностью значительно быстрее и проще вычислять некоторые показатели.

В) Обнаружение неизвестных причинных связей.

При решении этой задачи необходимо учитывать своеобразие взаимоотношений в причинно-следственном комплексе и особенности научно-методологических правил статистического исследования, опирающегося на количественные связи между явлениями. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждения об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей. При выводах следует обращать внимание на возможность появления ложной корреляции.

1.4. Линейная парная корреляция

Парная линейная корреляция является характеристикой меры линейной зависимости двух величин. При значении коэффициента корреляции =1 зависимость линейная функциональная (одному значению величины соответствует одно значение величины ). Облако точек, обладающих линейной функциональной зависимостью, приведено на рисунке 2.1.

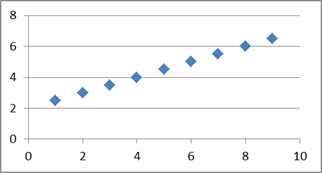
Рисунок 2.1 – Облако точек, обладающих линейной функциональной зависимостью =1.

При уменьшении коэффициента корреляции одному значению величины соответствует уже определенный закон распределения величины , что, при визуализации выборочных данных, дает разброс значений величины , однако линейный тренд при этом сохраняется (рис. 2.2).

Рисунок 2.2 – Облако точек. =0,93.

Чем ближе значение коэффициента корреляции к нулю, тем больше рассеяние. На рисунке 2.3 изображено облако точек при значении =0,04.

Рисунок 2.3 – Облако точек. =0,04.

Для вычисления коэффициента парной линейной корреляции следует вычислить выборочные средние для каждой из образующих облако 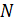точек величин и :

, ,

выборочные дисперсии:

, ,

средние квадратические отклонения:

, .

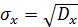Далее вычисляются выборочный корреляционный момент и выборочный коэффициент корреляции:

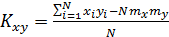, (2.1)

Выборочный корреляционный момент характеризует тесноту связи между величинами, однако его значение зависит от масштаба значений соответствующих величин. При делении корреляционного момента на произведение среднеквадратических отклонений осуществляется его нормирование, то есть нормированное значение – коэффициент корреляции, всегда будет находиться в интервале от -1 до 1, что обеспечивает универсальность характеристики тесноты связи и ее независимость от масштаба образующих зависимость величин.

1.5. Анализ частных связей

Изложение анализа частных связей начнем с примера [1]. В средине прошлого века, при анализе большого числа наблюдений, анализе большого числа наблюдений, относящихся к отливке труб на сталелитейных заводах, была установлена положительная корреляционная связь между временем плавки и процентом забракованных труб. Дать какое либо причинное истолкование этой стохастической связи было невозможно, а поэтому рекомендации ограничить продолжительность плавки для снижения процента забракованных труб выглядели малосостоятельными. Спустя несколько лет обнаружили, что большая продолжительность плавки всегда была связана с использованием сырья специального состава. Этот вид сырья приводил одновременно к длительному времени плавки и большому проценту брака, хотя оба эти фактора взаимно независимы.

Таким образом, высокий коэффициент корреляции между продолжительностью плавки и процентом забракованных труб полностью обусловливался влиянием третьего, не учтенного при исследовании фактора — характеристики качества сырья. Если же этот фактор был бы с самого начала учтен, то никакой значимой корреляционной связи между временем плавки и процентом забракованных труб не было бы обнаружено. Такую корреляцию между двумя переменными часто называют «ложной».

Для того, чтобы избавиться от влияния неучтенных переменных, и одновременно получить оценку тесноты связи между интересующими переменными, вычисляют значения частных (или очищенных) коэффициентов корреляции.

Частная корреляция позволяет определить тесноту связи между двумя переменными при фиксированном значении или исключении влияния остальных переменных. Иными словами, если между величинами и существует тесная связь, и, кроме того, зависит от , то будет так же коррелировать и с . Вполне возможно, что корреляция между и не прямая, а косвенная, обусловленная воздействием переменной . Поэтому необходимо исследовать частную корреляцию между и , исключив влияние переменной на .

Для нахождения коэффициента частной корреляции между и , при исключении влияния переменной , следует воспользоваться выражением:

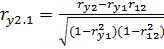
По аналогии можно легко выписать выражения для других коэффициентов частной корреляции. Таким образом, вычисление коэффициентов частной корреляции сводится к вычислению коэффициентов парной корреляции [11].

Обобщенное выражение:

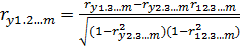(2.2)

1.6. Анализ множественных связей

Как уже говорилось ранее, при решении практических задач анализа данных, как правило, сталкиваются со сложными взаимосвязями между явлениями. Отсюда возникает задача определения тесноты связи между более чем двумя явлениями. Для этой цели используется коэффициент множественной корреляции, который характеризует тесноту связи одной из переменных с совокупностью других.

Для вычисления множественного коэффициента корреляции можно воспользоваться очень удобным для практических вычислений выражением:

(2.3)

Очевидно, с помощью этого выражения можно вычислить совокупный коэффициент корреляции, который характеризует тесноту связи переменной с совокупностью переменных и . Иными словами, можно получить оценку тесноты связи при условии, что переменная одновременно зависит от и . Коэффициент множественной корреляции всегда заключен в интервале от 0 до 1. С помощью этого коэффициента нельзя сделать вывод о положительной или отрицательной корреляции между переменными. Только если все коэффициенты парной корреляции имеют одинаковый знак, то этот же знак можно отнести так же к множественному коэффициенту корреляции. Чем больше значение приближается к единице, тем взаимосвязь сильнее. Для случая, когда 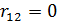, множественный коэффициент корреляции равен 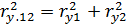, то есть если независимые переменные не коррелированы, квадрат коэффициента множественной корреляции равен сумме квадратов коэффициентов парных корреляций. Другими словами, он равен сумме интенсивности парных связей между и , а так же между и .

Выражение для коэффициента корреляции для любого числа независимых переменных:

,

или в матричном виде:

где , [1].

1.7. Измерение степени тесноты связи при нелинейной зависимости

Если между исследуемыми явлениями существуют нелинейные соотношения, то, так же как в случае линейной связи интересуются теснотой зависимости, ей силой. Если соотношения исследуемых явлений отличаются от линейных, то коэффициент корреляции, в принятой для линейной связи форме, не сможет отражать меру зависимости. На рисунке 2.4 приведен пример облака точек с нелинейной зависимостью. Коэффициент парной линейной корреляции =0,16.

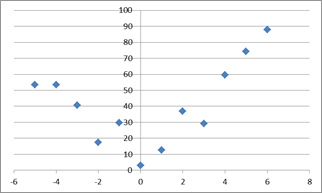
Рисунок 2.4 – Нелинейная зависимость переменных

В связи с тем, что большинство исследуемых и подвергающихся анализу данных имеют нелинейный характер, существует необходимость в применении достоверного показателя интенсивности связи. Таким показателем связи может служить индекс корреляции.

Индекс корреляции всегда находится в интервале [0,1] и вычисляется по формуле:

,

где - количество наблюдений, - ордината i-го наблюдения, - ордината i-го наблюдения, вычисленная с помощью функции регрессии при значении аргумента - абсцисса i-го наблюдения. В случае линейной регрессии . Очевидно, в этом случае индекс корреляции =1 [11].

1.8. Проверка значимости коэффициента корреляции

Для того чтобы сделать вывод о наличии или отсутствии корреляционной связи между исследуемыми переменными необходимо рассчитать значение выборочного коэффициента корреляции и выполнить проверку значимости его значения.

Процедура проверки значимости начинается с формулировки нулевой гипотезы . Она заключается в том, что между параметром выборки и параметром генеральной совокупности нет каких либо существенных различий. Альтернативная гипотеза состоит в том, что между этими параметрами имеются существенные различия. Например, при проверке наличия корреляции в генеральной совокупности нулевая гипотеза заключается в том, что истинный коэффициент корреляции равен нулю (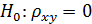). Если в результате проверки окажется, что нулевая гипотеза не приемлема, то выборочный коэффициент корреляции значимо отличается от нуля, то есть нулевая гипотеза отвергается и принимается альтернативная. При проверке значимости исследователь устанавливает уровень значимости , который дает определенную практическую уверенность в том, что ошибочные заключения будут сделаны в очень редких случаях.

При определенных предпосылках выборочный коэффициент корреляции связан со случайной величиной , подчиняющейся распределению Стьюдента. Вычисленная по результатам обработки эмпирических наблюдений статистика

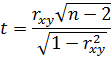
сравнивается с критическим значением, определяемым по таблице распределения Стьюдента при заданном уровне значимости и степенях свободы. Если вычисленное , то нулевая гипотеза при уровне значимости отвергается, т.е. связь между переменными значима. В противном случае нулевая гипотеза при уровне значимости принимается. Отклонение от 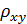=0 можно приписать случайной вариации [4, 11].

2.9. Понятие регрессии

Корреляция и регрессия тесно связаны между собой. Это привело к тому, что иногда регрессию рассматривают как частный случай корреляции, считая тем самым корреляцию более широким понятием. Однако большинство авторов придерживаются мнения, что ход рассуждений и постановка задач в корреляционном и регрессионном анализе различны.

Различают два вида зависимостей между явлениями и процессами: а) функциональную зависимость и б) стохастическую зависимость. В случае функциональной зависимости имеется однозначное отображение элементов множества А в элементы множества В. Множество А называют областью определения, а множество В – множеством значения функции. При стохастической зависимости каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловлено тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов, а так же погрешностью измерений. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью. Таким образом, появляющиеся значения зависимой переменной являются, по сути, реализациями случайной величины.

Можно сделать вывод, что регрессия – это односторонняя стохастическая зависимость. Например, при изучении зависимости курса иностранной валюты от стоимости единицы энергоносителя на международных биржах речь идет об односторонней связи, следовательно, о регрессии. Обе переменные являются случайными. Каждому значению соответствует множество значений и наоборот, каждому значению соответствует множество значений .

При функциональной зависимости факторный признак полностью определяет результативный признак , кроме того, при функциональной зависимости функция обратима. В случае со стохастической зависимостью факторный признак лишь определяет условный закон распределения признака . Кроме того, функция регрессии необратима. Если в предыдущем примере факторный признак – стоимость единицы энергоносителя , а результативный – курс иностранной валюты , то говорят о регрессии на . Если же наоборот факторный признак – стоимость курса иностранной валюты, а результативный – стоимость единицы энергоносителя то говорят уже о регрессии на , то есть исследуется влияние стоимости курса иностранной валюты на стоимость единицы энергоносителя.

Функция регрессии формально устанавливает соответствие между переменными, хотя они могут не состоять в причинно-следственных отношениях. Однако задача аналитического исследования заключается в определении причинных зависимостей. Только понимание истинных причин явлений придает результатам анализа действенный характер, позволяет предвидеть явления, учитывать или надлежащим образом изменять их.

2.10. Виды регрессии

Различные виды регрессии [11]:

Относительно числа явлений:

А) Простая (парная);

Б) Множественная или частная.

Относительно формы зависимости:

А) Линейная;

Б) Нелинейная.

Относительно характера:

А) Положительная;

Б) Отрицательная.

Относительно типа соединения явлений:

А) Непосредственная;

Б) Косвенная;

В) Ложная регрессия.

2.11. Задачи регрессионного анализа

А) Установление формы зависимости.

При решении этой задачи зависимость описывается «в первом приближении»: оценивается, как правило, вид регрессии.

Б) Определение функции регрессии.

При изучении стохастической зависимости данных каждому значению объясняющей переменной может соответствовать распределение значений зависимой переменной. Важно не только указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов причин, если бы прочие (второстепенные) факторы не изменялись. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.

В) Оценка неизвестных значений зависимой переменной.

С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (решить задачу интерполяции) или оценить течение процесса вне заданного интервала (решить задачу экстраполяции). Эти задачи решаются путем подстановки в соответствующие уравнения регрессии с найденными оценками параметров значений объясняющих переменных. Результат представляет оценку значения зависимой переменной.

2.12. Парная линейная регрессия

В общем случае, как уже отмечено, под регрессией понимают одностороннюю стохастическую зависимость одной случайной переменной от другой (парная регрессия) или нескольких (множественная регрессия) случайных переменных. Математическое решение задачи описания зависимости сводится к получению функции регрессии.

При анализе зависимости двух переменных целесообразно построить диаграмму рассеяния (облако точек). По оси абсцисс отмечают значения независимой переменной, по оси ординат - зависимой. Результат каждого наблюдения отображается точкой на плоскости. Совокупность этих точек образует скопление (облако). Облако точек определяет картину зависимости двух переменных. По ширине разброса точек можно сделать вывод о степени тесноты связи (рис. 2.1-2.3). Для того, чтобы по диаграмме рассеяния графическим путем определить функцию регрессии, нужно натянуть воображаемую нить так, чтобы по обе стороны от нее оказалось приблизительно одинаковое число точек. Нить должна обязательно проходить через центр рассеяния (рисунок 3.1).

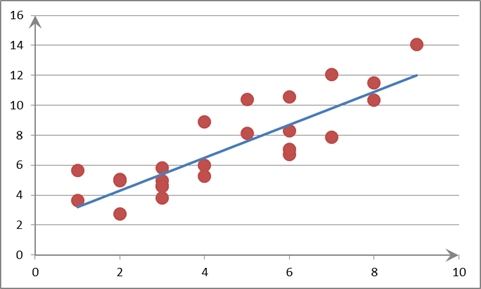
Рисунок 3.1 – Диаграмма рассеяния

Разумеется, такой подход является весьма субъективным и приближенным, поэтому для построения регрессионного уравнения применяются специальные методы.

Если при исследовании расположения точек на диаграмме предполагается линейный характер зависимости, то эту зависимость выражают с помощью функции линейной регрессии:

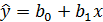(3.1)

Здесь - объясняющая переменная. Имеется наблюдений над этой переменной (). Неизвестные параметры регрессии подлежат оценке. называется постоянная регрессии, определяет точку пересечения прямой регрессии с осью ординат. Коэффициент 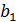- коэффициент регрессии. Он характеризует наклон регрессионной прямой к оси ОХ. Коэффициент регрессии является мерой влияния, оказываемого изменением переменной на переменную . Согласно уравнению (3.1) 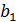указывает среднюю величину изменения переменной при изменении объясняющей переменной на единицу (рисунок 3.2).

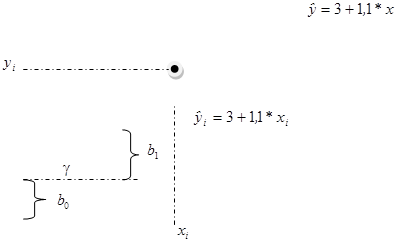
Рисунок 3.2 – Регрессионная прямая и ее параметры

Знак 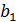определяет направление этого изменения. При положительном коэффициенте регрессии делают вывод о положительной линейной регрессии, означающей увеличение в среднем зависимой переменной при увеличении значения объясняющей переменной . При отрицательном коэффициенте регрессии, наоборот, зависимая переменная в среднем убывает с увеличением объясняющей переменной .

Таким образом, значения функции регрессии 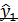указывают средние значения зависимой переменной при заданном значении объясняющей переменной .

Очевидно, различным значениям и 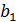будут соответствовать различные линии. Из бесконечного множества прямых, которые можно провести на плоскости, следует выбрать одну, наилучшим образом соответствующую опытным данным. Для нахождения коэффициентов прямой можно воспользоваться методом наименьших квадратов.

2.13. Построение регрессионной прямой с помощью метода наименьших квадратов

Нахождение прямой, наилучшим образом соответствующей опытным

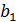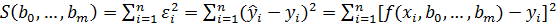данным, предполагает нахождение коэффициентов и линейной функции, при которых некоторый критерий достигает минимального значения. В качестве критерия принимают сумму квадратов всех уклонений и (см. рисунок 3.2):

(3.2)

Определение параметров при такой мере расхождения между опытными и теоретическими значениями называется методом наименьших квадратов.

Очевидно, функция (3.2) является функцией двух переменных и 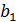. Известно, что для нахождения экстремума функции нескольких переменных необходимо взять частные производные по каждой из переменных и приравнять их нулю. В результате получится система уравнений:

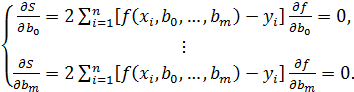(3.3)

Проще всего система (3.3) выглядит при линейной зависимости. В ней два параметра и 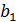и, следовательно, в системе будет всего два уравнения:

После преобразований получаем:

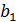Известно, что главный определитель такой системы отличен от нуля, поэтому коэффициенты и определяются однозначно [1, 11].

2.14. Множественная линейная регрессия

При анализе данных, в большинстве случаев, выясняется, что каждое явление определяется действием не одной причины, а нескольких, и даже комплексом причин. Поэтому стоит задача исследования зависимости одной зависимой переменной от нескольких объясняющих переменных . Эту задачу можно решить с помощью множественного, или многофакторного регрессионного анализа.

При существовании линейного соотношения между переменными уравнение множественной регрессии в общем виде записывается таким образом:

(3.4)

Объясняющие переменные оказывают совместное одновременное влияние на зависимую переменную [11].

В выражении (3.4) 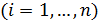- расчетные значения регрессии. Они указывают средние значения переменной в точке при фиксированных значениях объясняющих переменных 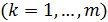в предположении, что только эти переменных являются причиной изменения переменной . Значения представляют собой оценки средних значений для фиксированных значений переменных в точке .

Коэффициенты 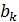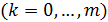- параметры регрессии в (3.4). Постоянная регрессии снова выполняет в уравнении регрессии функцию выравнивания. Она определяет точку пересечения гиперповерхности регрессии с осью ординат.

Значения 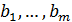- представляют собой оценки коэффициентов регрессии. Индекс при коэффициенте соответствует индексу объясняющей переменной. Так, 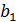указывает среднюю величину изменения при изменении на единицу при условии, что другие переменные остаются без изменения. 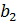показывает, на сколько единиц в среднем изменится , если бы переменная изменилась на единицу при условии, что другие переменные остались бы без изменения и т.д.

Для нахождения коэффициентов множественной регрессии будем исходить из выражения (3.4). Для постоянной в уравнении регрессии можно ввести фиктивную переменную , принимающую значение, равное 1, для всех 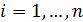: . Линейную модель зависимости можно представить в виде

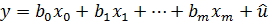(3.5)

где 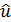- аддитивная составляющая – возмущающая переменная, дающая суммарный эффект от воздействия всех неучтенных факторов и случайностей. Результаты наблюдений следует представить в виде вектор-столбца размерности . Значения объясняющих переменных 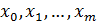в виде матрицы размерности , остатки функции регрессии в виде вектор столбца размерности . Искомые параметры регрессии образуют вектор-столбец размерности :

; ; ;

Функция регрессии (3.4) может быть представлена более компактно в матричной форме:

, (3.6)

а функция (3.5) – соответственно:

В результате применения метода наименьших квадратов для оценки неизвестных параметров в (3.6) будет получено выражение [11]:

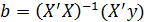(3.7)

;

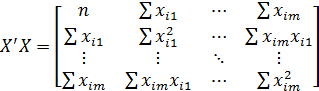2.15. Нелинейная регрессия

Между явлениями и процессами не всегда существуют линейные соотношения. В таких случаях для описания зависимости используют нелинейную корреляцию и регрессию. Односторонняя стохастическая зависимость может быть описана, например, с помощью полиномиальной регрессии:

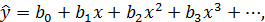
либо с помощью гиперболический регрессии:

.

Так же применяются степенная, показательная, логарифмическая и тригонометрические функции. Подбор функции регрессии должен выполняться с учетом особенностей предметной области, которой принадлежат анализируемые данные.

Различают два класса нелинейных регрессий. К первому классу можно отнести регрессии, нелинейные относительно включенных в анализ объясняющих переменных , но линейные по неизвестным, подлежащим оценке параметрам регрессии 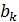. Образующие этот класс нелинейные регрессии называют так же квазилинейными регрессиями. Для них возможно непосредственное применение МНК.

Второй класс регрессий характеризуется нелинейностью по оцениваемым параметрам. Этот класс регрессий часто встречается при исследовании экономических явлений и не допускает применения обычного МНК. Однако некоторые функции с помощью преобразования переменных поддаются линеаризации и последующему применению МНК.

2.16. Значимость коэффициентов множественной регрессии

При проверке значимости коэффициентов множественной регрессии выдвигают гипотезы:

, т. е. нет существенного различия между оценкой параметра регрессии, полученной по результатам выборки 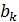и истинным значением параметра регрессии генеральной совокупности ;

, т.е. имеется значимая разница между оценкой параметра регрессии и соответствующим значением генеральной совокупности.

При определенных предпосылках [11] оценки параметров имеют t-распределение. При соблюдении этих предпосылок для проверки значимости оценок параметров, входящих в уравнение регрессии, применяется t-критерий:

,

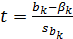где - стандартное отклонение оценки параметра регрессии 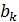. Полученное значение t-критерия сравнивают с критическим значением для заданного уровня значимости и числа степеней свободы . Если то 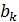значимо отличается от , то есть нельзя предположить, что выборка отобрана из генеральной совокупности с параметром регрессии .

Когда заранее указано числовое значение параметра регрессии генеральной совокупности, то выдвигают другое предположение:

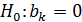, т. е.