Тема 3. Модель парной регрессии
Вопросы:
1. Общие сведения о регрессионном анализе
2. Реализация основных этапов построения и анализа парной линейной регрессии
3. Парная нелинейная регрессия
Общие сведения о регрессионном анализе
Регрессионный анализ предназначен для исследования количественных взаимосвязей переменных и представления их в виде регрессионной модели.
Виды регрессий:
1) по числу переменных:
- парная,
- множественная,
- частные;
2) по виду связи:
- линейная,
- нелинейная;
3) по направлению связей:
- положительная,
- отрицательная.
Задачи регрессионного анализа:
1. Установление формы связи, построение модели.
2. Оценка качества моделей.
3. Распределение факторов по степени влияния на показатель.
4. Построение прогноза.
Общий вид регрессионной модели:
. (1)
Если в уравнении (1) присутствует только один фактор X, а f – линейная математическая функция, получим парную линейную модель регрессии вида
, (2)
где 
– свободный член в модели, 
– коэффициент регрессии, который показывает, на сколько единиц изменится Y приизменении фактора X на 1 единицу. При >0 связь между переменными прямая (регрессия положительная), при <0 связь между переменными обратная (регрессия отрицательная). 
– ошибки моделирования (остатки).
Основные этапы построения и анализа модели (2):
1. Оценка параметров. Определение вида модели.
2. Проверка качества модели.
3. Оценка статистической значимости уравнения и параметров.
4. Определение степени влияния фактора Х на показательY.
5. Экономический прогноз.
Реализация основных этапов построения и анализа парной линейной регрессии
1. Оценка параметров. Определение вида модели.
Для оценки параметров линейных моделей применяют МНК. Он позволяет так подобрать коэффициенты и , чтобы теоретические значения исследуемого показателя (линия регрессии) находились на минимальном расстоянии от фактических данных (рис.1).
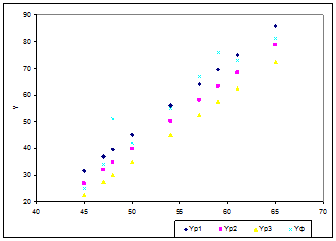
Рис. 1. Расположение линии регрессии относительно фактических значений исследуемого показателя
Как видно из рисунка 1, линий регрессии можно провести очень много. Важно, чтобы выбранная линия более всего соответствовала фактическим данным по всей их совокупности. Такую линию и позволяет подобрать МНК.
Аналитически, оценки и методом наименьших квадратов находятся путем минимизации функции
.
Минимизация функции Q сводится к математической задаче определения точки минимума двух переменных. Эта задача решается нахождением производных функции по каждой переменной (частных производных) и приравнивании их к нулю:
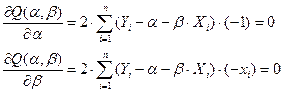
Получилась система из двух уравнений с двумя переменными и , решение которой дает следующие формулы для расчета параметров уравнения парной линейной регрессии
Найденное решение существует, если
Это условие называется условием идентифицируемости модели. Оно означает, что не все значения 
совпадают между собой и со своим средним. Если оно не выполняется, то все точки 
лежат на одной вертикальной прямой 
(рис.2).
Рис. 2. Условие идентифицируемости не выполняется
Пример.
Пусть зависимая переменная Y – прибыль некоторой компании (исходные данные приведены в таблице 1), а фактор X – объем продаж товара этой компании.
Требуется:
1) найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии;
2) вычислить остатки, найти остаточную сумму квадратов, оценить дисперсию остатков 
, построить график остатков;
3) проверить выполнение предпосылок МНК;
4) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( =0,05);
5) вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ( =0,05), найти среднюю относительную ошибку аппроксимации, сделать вывод о качестве модели;
6) осуществить прогнозирование среднего значения показателя Y при уровне значимости =0,1, если прогнозное значение фактора составит 117 % от его максимального значения;
7) представить графически фактические, расчетные и прогнозные значения.
Решение:
1) найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии:
Для решения задачи построим расчетную таблицу 1:
Таблица 1
| № п.п. | Y | X | X-Xcp | (X-cp)^2 | Y-Ycp | (X-Xcp)* (Y-Ycp) | Yp | e | e^2 | eотн | (Y-Ycp)^2 | X^2 |
| -9 | -31 | 31.65 | -6.65 | 44.22 | 26.6 | |||||||
| -7 | -22 | 37.07 | -3.07 | 9.425 | 9.03 | |||||||
| -4 | -14 | 45.2 | -3.2 | 10.24 | 7.62 | |||||||
| -6 | -5 | 39.78 | 11.22 | 125.9 | ||||||||
| -1 | 56.04 | -1.04 | 1.082 | 1.89 | ||||||||
| 64.17 | 2.83 | 8.009 | 4.22 | |||||||||
| 75.01 | -2.01 | 4.040 | 2.75 | |||||||||
| 69.59 | 6.41 | 41.09 | 8.43 | |||||||||
| 85.85 | -4.85 | 23.52 | 5.99 | |||||||||
| Сум-ма | -0.36 | 267.5 | 88.54 | |||||||||
| Среднее | 9.84 |
уравнение регрессии:
Y=-90.3+2.71*X,
экономический смысл коэффициента регрессии:
при изменении объема продаж компании (Х) на 1 единицу прибыль (Y) будет меняться в ту же сторону на 2,71 единиц.
Замечание.
Уравнение регрессии и целый ряд его характеристик можно получить, воспользовавшись инструментом Регрессия в пакете Анализ данных в Excel (см. отчет по регрессионному анализу).
2) вычислить остатки, найти остаточную сумму квадратов, оценить дисперсию остатков , построить график остатков:
Замечание:
В эконометрике рассматривается значительное количество различных видов дисперсий. Дисперсия – это величина, характеризующая степень отклонения (разброса, рассеяния) каких-либо величин друг относительно друга. В зависимости от величин, различают дисперсии:
1) общая дисперсия результативного признака Y характеризует степень отклонения фактических значений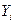 
исследуемой переменной от их среднего значения 
(рис.3):
.
Рис.3. Общая дисперсия результативного признака
2) объясненная (факторная) дисперсия характеризует степень отклонения расчетных значений 
исследуемой переменной от среднего значения (рис.4):
,
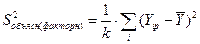где k – число независимых факторов в уравнении регрессии, в парной регрессии k=1.
Рис. 4. Объясненная (факторная) дисперсия
Из рисунка 4 видно, что факторная дисперсия позволяет оценить степень отклонения линии регрессии от линии, соответствующей .
3) остаточная дисперсия (дисперсия остатков) оценивает степень отклонения линии регрессии от фактических значений 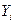исследуемого показателя (рис.5):
,
где k – число факторов в уравнении регрессии.
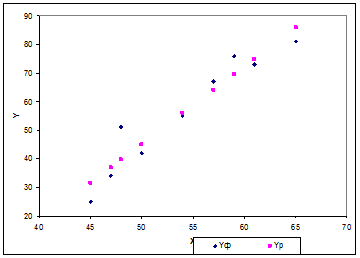
Рис.5. Остаточная дисперсия
Все названные дисперсии связаны соотношением
.
Остатки:
Остаточная сумма квадратов:
.
Дисперсия остатков:
Корень из дисперсии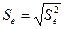 
называется среднеквадратическим отклонением (СКО) или стандартной ошибкой модели:
.
График остатков:
См. также регрессионный анализ в Excel.
2. Проверка качества модели
Основную информацию для оценки качества регрессионных моделей содержит ряд отклонений фактических уровней выборочной совокупности от их расчетных значений (ряд остатков 
). Это связано с тем, что параметры регрессионного уравнения, а, значит, и случайные остатки, должны обладать определенными свойствами. Они должны быть несмещенными, состоятельными и эффективными.
Несмещенность оценок – математическое ожидание остатков равно 0.
Эффективность – оценки характеризуются наименьшей дисперсией.
Состоятельность – увеличение точности оценок с увеличением объема выборки.
Исследование ряда остатков на наличие этих свойств предполагает проверку следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) независимость остатков или отсутствие их автокорреляции;
3) остатки подчиняются нормальному распределению;
4) нулевая средняя величина остатков (или их математическое ожидание), не зависящая от уровней фактора Х;
5) гомоскедастичность остатков – дисперсия каждого отклонения одинакова для всех значений фактора.
Проверка первых четырех предпосылок представляет собой исследование адекватности модели определенным статистическим критериям. Этот материал подробно рассмотрен в курсе ЭММиПМ.
Рассмотрим подробнее исследование гомоскедастичности остатков. Дисперсия остатков считается гомоскедастичной, если для каждого значения фактора остатки имеют одинаковую дисперсию. В этом случае на графике остатков они расположены в виде горизонтальной полосы (рис.5).
Рис. 6. Гомоскедастичные остатки
Если это условие не соблюдается, то имеет место гетероскедастичность. Рассмотрим наглядные примеры гетероскедастичности остатков (рис. 6 а, 6 б).
а) б)
Рис. 7. Гетероскедастичные остатки
При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда – Квандта, разработанный в 1965 году. Тест, предложенный этими учеными, включает в себя следующие шаги:
1. Упорядочение n наблюдений по мере возрастания переменной X.
2. Исключение из рассмотрения С центральных наблюдений; при этом (n-C):2>p, где р – число оцениваемых параметров (
).
3. Разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями фактора Х) и определение по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения: R=S1:S2 (в числителе должна стоять большая величина).
Вывод о гомоскедастичности делается с помощью F-критерия Фишера с (n-C-2p):2 (р – число оцениваемых в уравнении параметров; для парной регрессии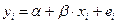 
р=2) степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Протестируем данные нашего примера на наличие гомоскедастичности остатков.
Пример (продолжение).
3) проверить выполнение предпосылок МНК:
Проверку предпосылок 1 – 4 выполнить самостоятельно, используя материал дисциплины ЭММиПМ.
Проверка предпосылки 5:
| 1. Упорядочим Y по мере возрастания Х | (данные - | сортировка): | |||||||
| Y | X | Y | X | ||||||
| 2. Исключаем из рассмотрения С=1 центральное наблюдение. | |||||||||
| 3. Разделим совокупность из 9-1=8 наблюдений на две группы и определим по каждой уравнения регрессии: | |||||||||
| Таблица 2 | |||||||||
| Уравнения | Y | X | Yp | e | e^2 | ||||
| y=-148,35+3,9x | 28.19231 | -3.19231 | 10.19083 | ||||||
| 36.03846 | -2.03846 | 4.155325 | |||||||
| 39.96154 | 11.03846 | 121.8476 | |||||||
| 47.80769 | -5.80769 | 33.72929 | |||||||
| Сумма | 169.9231 | ||||||||
| y=16,5+1,5x | -2 | ||||||||
| -2 | |||||||||
| -3.3E-13 | 1.07E-25 | ||||||||
| Сумма | |||||||||
| 4. R=169,9/24= | 7.080128 | ||||||||
| Число степеней свободы: | (9-1-2*2):2=2 | ||||||||
| Fтаб(0,05;2;2)= | |||||||||
| Fтаб>R | |||||||||
| Вывод: подтверждается наличие гомоскедастичности в остатках. |
Для анализа качества регрессионных моделей используется ряд дополнительных характеристик. К ним относится, например, индекс корреляции:
.
Этот коэффициент является универсальным, так как отражает тесноту связи и точность модели может использоваться при любой форме связи переменных. На практике чаще используется его квадрат, который называется коэффициентом детерминации:
.
, иногда 
выражают не в долях, а в процентах.
Коэффициент детерминации показывает,какая доля вариации (случайных колебаний, общей дисперсии) признака Y учтена в построенной модели и обусловлена случайными колебаниями включенных в нее факторов. Качество модели тем лучше, чем ближе к 1. Иными словами характеризует степень влияния включенных в модель факторов. Влияние факторов, не учтенных в модели, определяется тогда величиной 1- . Модель тем лучше, чем больше и меньше 1- .
3. Проверка статистической значимости уравнения регрессии и его параметров
а) проверка статистической значимости уравнения:
Проверка значимости (существенности) уравнения регрессии позволяет установить, существенна ли связь включенных в уравнение признаков (Y и X), соответствует ли математическая модель, выражающая зависимость Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y.
Оценка значимости уравнения регрессии в целом проводится с помощью F-критерия Фишера:
или в терминах коэффициента детерминации
,
где n – длина совокупностей данных, k – количество факторов, включенных в модель (в уравнении парной регрессии k=1).
Уравнение регрессии статистически значимо, если
.
Замечания:
1) 
определяется максимальной величиной отношения дисперсий 
, которая может иметь место при случайном их расхождении;
2) для определения можно использовать статистическую функцию FРАСПОБР, предварительно задав три параметра 
, где – заданный уровень значимости проверки или уровень вероятности ( связано с вероятностью Р формулой 
); 
– число степеней свободы числителя, равное количеству k факторов, включенных в модель; 
– число степеней свободы знаменателя (n-k-1). Таким образом, зависит от заданной вероятности, числа уровней в совокупностях данных и вида уравнения регрессии;
3) оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (см. отчет по регрессионному анализу в Excel).
Пример (продолжение).
5) вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ( =0,05), найти среднюю относительную ошибку аппроксимации, сделать вывод о качестве модели
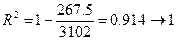
вывод: 91,4 % случайной вариации исследуемого признака Y учтено в построенной модели и обусловлено случайными колебаниями включенного в нее фактора Х;
вывод: уравнение регрессии статистически значимо, связь включенных в него признаков существенна;
из таблицы 1 имеем:
вывод: фактические значения прибыли Y отличаются от модельных 
в среднем на 9.8 %; уровень точности модели недостаточный.
а) проверка статистической значимости параметров уравнения:
В линейной регрессии обычно оценивается значимость не только уравнения регрессии, но и отдельных его параметров. Для этого применяется t-критерий Стьюдента:
1) рассчитывают стандартные ошибки (среднеквадратические отклонения) 
и 
каждого из параметров уравнения 
по формулам
, 
,
где 
– рассмотренная выше остаточная дисперсия;
2) определяют расчетные значения t-критерия Стьюдента:
, 
;
3) определяют табличное значение t-критерия 
с помощью статистической функции СТЬЮДРАСПОБР по двум параметрам: заданному уровню значимости и одной степени свободы (n-k-1);
4) параметры уравнения регрессии будут статистически значимы, если выполняются неравенства:
, 
.
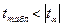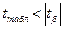Замечания:
1) статистическая значимость (незначимость) коэффициента регрессии означает одновременно статистическую значимость (незначимость) фактора Х, включенного в уравнение; статистически незначимый (или несущественный) фактор должен быть устранен из модели или заменен другим;
2) статистическая значимость (незначимость) параметра уравнения означает неверную спецификацию модели, под которой понимают:
а) выбор вида уравнения;
б) определение независимых факторов для включения в модель;
3) t-критерий можно использовать также для определения интервальных оценок параметров модели:
,
.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, то есть не должны содержать одновременно положительные и отрицательные величины и даже нуль.
Пример (продолжение).
3) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( =0,05)
Вывод: оба параметра модели статистически значимы.
Дополнение: интервальные оценки параметров
Замечание:
Расчетные значения t-критерия, а также интервальные оценки параметров можно найти в отчете по результатам работы с инструментом Регрессия (показать).
4. Определение степени влияния фактора Х на показательY
Для определения степени влияния фактора Х на показатель Y используют коэффициент эластичности
.
В случае парной линейной регрессии производная определяется по формуле
,
Тогда формула для эластичности примет вид
.
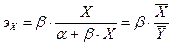Эластичность показывает: на сколько процентов изменится исследуемый признак Y при изменении фактора Х на 1 %. Положительное значение эластичности свидетельствует о прямой связи между переменными, отрицательное – об обратной. При 
изменение Y по Х считается эластичным, при 
– неэластичным (например, неэластичен спрос по цене на товары первой необходимости: хлеб, молоко, лекарства и др.; эластичный спрос по цене имеем на предметы роскоши).
В нашем примере эластичность равна
%.
Это означает, что при изменении объема продаж Х на 1 % прибыль Y изменится в ту же сторону на 2,6 %. Изменение эластично.
5. Экономический прогноз
Рассматриваемая модель может быть использована для определения прогнозных оценок исследуемой величины. При прогнозировании на основе регрессионных моделей можно выделить три основных этапа:
1) точечный прогноз фактора Х;
2) точечный прогноз показателя Y;
3) интервальный прогноз показателя Y.
Рассмотрим содержание этих этапов подробнее.
1) точечный прогноз фактора Х в зависимости от специфики исходных данных и условия задачи можно определить одним из следующих способов:
а) если исходные данные являются временными рядами, то для прогноза фактора можно воспользоваться методами экстраполяции и использовать наиболее подходящую модель временного ряда
.
Тогда прогноз фактора на k шагов вперед определяется по формуле
.
б) вслучае временных рядов 
можно найти также с помощью среднего абсолютного прироста (САП) по формуле
.
в) если исходные данные являются пространственными, то, очевидно, в задаче будет задано правило для определения 
. Например, прогнозное значение фактора составляет 80 % от его среднего значения. Тогда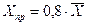 
.
2) точечный прогноз показателя Y находят подстановкой в модель прогнозных значений фактора:
– в случае пространственных данных,
– в случае временных рядов.
3) интервальный прогноз показателя Y:
вначале находят ошибку прогнозирования
,
которая зависит от стандартной ошибки модели 
, удаления от своего среднего значения, количества наблюдений n, заданного уровня вероятности попадания в интервал прогноза (он определяет величину 
;
затем находят сам доверительный интервал прогноза:
нижняя граница интервала – 
,
верхняя граница интервала – 
.
Пример (продолжение).
6) осуществить прогнозирование среднего значения показателя Y при уровне значимости =0,1, если прогнозное значение фактора Х составит 117 % от его максимального значения
1) точечный прогноз фактора Х
,
2) точечный прогноз показателя Y
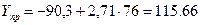
3) интервальный прогноз показателя Y
Нижняя граница интервала: 115,66-17,97=97,69
Верхняя граница интервала: 115,66+17,97=133,63.
представить графически фактические, расчетные и прогнозные значения
| 
|