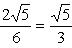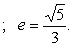КРИВЫЕ ВТОРОГО ПОРЯДКА
-- это уравнение определяет на плоскости окружность, эллипс, гиперболу и параболу.
Окружность.
- каноническое уравнение окружности
- уравнение окружности с центром в начале координат
- общее уравнение окружности
Для уравнения окружности выполнимо два условия:
1. коэффициенты при x и y равны между собой
2. отсутствует произведение текущих координат вида x*y.
Эллипс.
Эллипс – множество всех точек плоскости, сумма расстояний от каждой из которых до двух фокусов – величина постоянная и большая, чем расстояние между фокусами.
- каноническое уравнение эллипса
Основные понятия, связанные с уравнением эллипса:
1. Эллипс симметричен относительно координатных осей и относительно начала координат.
2. Точки пересечения с осью Ox 
, 
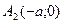, а с осью Oy 
, 
.
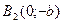3. Точки 
- вершины эллипса.
4. Отрезки 
и 
, а также их длины 2a и 2b называются большой и малой осями эллипса. Числа a и b – большой и малой полуосями.
5. Все точки эллипса лежат внутри прямоугольника, образованного прямыми x = -a, x = a, y = -b, y = b.
6. Если a>b, то эллипс вытянут вдоль оси Ox, а если a<b, то вдоль оси Oy.
Гипербола.
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до фокусов – величина постоянная, меньшая, чем расстояние между фокусами.
- каноническое уравнение гиперболы.
Основные понятия, связанные с уравнением гиперболы:
1. Гипербола симметрична относительно координатных осей и относительно начала координат.
2. Точки пересечения с осью Ox 
, ось Oy гипербола не пересекает.
3. Точки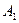 
и 
называются вершинами гиперболы.
4. Отрезок 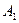= 2a, называется действительной осью. 
- действительная полуось. 
называется линейной осью, b – мнимая полуось.
|
|
5. Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы.
6. Прямые 
являются асимптотами. Ветви гиперболы стремятся к этим прямым, но не пересекают их.
7. При построении гиперболы целесообразно сначала построить оси прямоугольника гиперболы, провести его диагонали, которые будут асимптотами и отметить вершины , .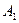
8. Гиперболы и 
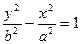называются сопряженными.
4. Парабола – множество всех точек, каждая из которых одинаково удалена от фокуса, и прямой, называемой директрисой.
Расстояние от фокуса до директрисы называется параметром параболы (P>0).
- каноническое уравнение параболы.
Основные понятия, связанные с уравнением параболы:
1. 
Поскольку в уравнении у в четной степени, парабола симметрична относительно оси Ox.
2. Т.к. P>0, то x 
0, значит парабола располагается справа от оси Oy.
3. При x =0, y = 0 парабола проходит через начало координат.
4. Точка (0:0) называется вершиной параболы.
Отрезок FM называется фокальным радиусом точки М.
Уравнение 
тоже определяет параболу.
Задача 30. Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
Решение:
Искомое уравнение имеет вид (x - a)2 + (y - b)2 = r 2. Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек, получим три уравнения для определения a, b и r. Вот эти уравнения:
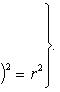
Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем
|
|
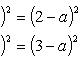
Раскрывая скобки и упрощая, будем иметь
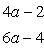
Отсюда
.
Подставляя эти значения a и b в первое из уравнений системы, получим
.
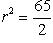Искомое уравнение имеет вид
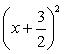
или после упрощений x 2 + y 2 + 3 x + 9 y - 10 = 0.
Задача 31. Составить простейшее уравнение эллипса, зная, что:
а) его полуоси a = 6, b = 4;
б) расстояние между фокусами 2 c = 10, а большая полуось 2 a = 16;
в) большая полуось a = 12, а эксцентриситет e = 0,5;
г) малая полуось b = 8, а эксцентриситет e = 0,6;
д) сумма полуосей a + b = 12, а расстояние между фокусами 
Решение:
а) Простейшее уравнение эллипса имеет вид
.
Подставляя сюда a = 6, b = 4, получим
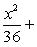
б) Имеем 2 c = 10; c = 5; 2 a = 16; a = 8.
Чтобы написать уравнение эллипса, следует найти малую полуось b. Между величинами a, b и c у эллипса существует зависимость a 2 - b 2 = c 2, или b 2 = a 2 - c 2. В нашем случае b 2 = 64 - 25 = 39, и уравнение эллипса будет иметь вид
в) a = 12; e = 0,5; известно, что 
; в этой формуле неизвестно c. Для его определения получаем уравнение
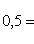
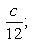
отсюда c = 6.
Теперь, зная, что a = 12, c = 6, пользуясь отношением a 2 - c 2 = b 2, найдем, что b 2 = 144 - 36 = 108; a 2 = 144.
Уравнение будет
.
г) b = 8; e = 0,6;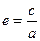 
, отсюда 
. Напишем соотношение a 2 - c 2 = b 2 и подставим в него c = 0,6 a; b = 8. Получим a 2 = 0,36 a 2 = 64; 0,64 a 2 = 64; a 2 = 100.
Уравнение эллипса будет иметь вид
д) a + b = 12, .
Для определения уравнения эллипса надо знать a и b. Нам известно, что 
; c 2 = 18; a 2 - b 2 = c 2.
Поэтому (a + b)(a - b) = 18. Подставляя сюда a + b = 12, найдем, что a - b = 1,5.
Решая систему уравнений
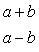
получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде
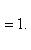
Задача 32. Найти длины осей, координаты фокусов и эксцентриситет эллипса 4 x 2 + 9 y 2 = 144.
|
|
Решение:
Преобразуем это уравнение к простейшему виду
.
Разделив обе части заданного уравнения на 144, получим
.
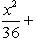
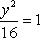Отсюда заключаем, что a 2 = 36, b 2 = 16. Значит, a = 6, 2 a = 12; b = 4, 2 b = 8. Зная a и b, из соотношения a 2 - c 2 = b 2 найдем c. Подставим a = 6; b = 4 и получим, что 
. Координаты фокусов будут 
и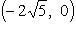 
. Эксцентриситет эллипса
