Метод простых итераций во всех рассмотренных вариантах использует для построения очередного приближения 
только информацию о функции в одной лишь точке 
; при этом никак не используются предыдущие значения 
Однако эту предыдущую информацию также можно использовать при нахождении . В качестве примера такого метода мы приведём метод, основанный на нахождении по двум предыдущим приближениям и 
с помощью линейной интерполяции, называемый методом хорд.
Идея метода состоит в том, что по двум точкам 
и 
построить прямую 
(то есть хорду, соединяющую две точки графика 
) и взять в качестве следующего приближения абсциссу точки пересечения этой прямой с осью 
. Иными словами, приближённо заменить на этом шаге функцию 
её линейной интерполяцией, найденной по двум значениям 
: и . (Линейной интерполяцией функции назовём такую линейную функцию 
, значения которой совпадают со значениями в двух фиксированных точках, в данном случае -- в точках и .)
В зависимости от того, лежат ли точки и по разные стороны от корня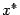 
или же по одну и ту же сторону, получаем такие чертежи:
13. Рис.9.14.Построение последовательного приближения по методу хорд: два случая
Итак, очередное последовательное приближение будет зависеть от двух предыдущих: 
. Найдём выражение для функции 
.
Интерполяционную линейную функцию будем искать как функцию с угловым коэффициентом, равным разностному отношению
построенному для отрезка между и , график которой проходит через точку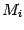 
:
Решая уравнение 
, находим
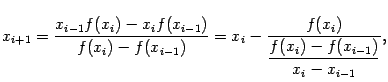
то есть
| (9.3) |
Заметим, что величина 
может рассматриваться как разностное приближение для производной 
в точке . Тем самым полученная формула (9.3) -- это разностный аналог итерационной формулы метода Ньютона.
Вычисление по формуле (9.3) гораздо предпочтительнее вычисления по другой полученной нами формуле
хотя эти две формулы математически тождественны, поскольку при использовании формулы (9.3) в случае вычислений с округлениями (например, на компьютере) достигается меньшая потеря значащих цифр.
Имеются две разновидности применения формулы (9.3).
Первая разновидность: вычисления ведутся непосредственно по формуле (9.3) при 
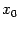, начиная с двух приближений 
и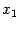 
, взятых, по возможности, поближе к корню 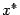. При этом не предполагается, что 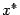лежит между 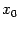и 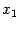(и что значения функции 
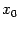в точках и 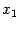имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между и на каком-либо следующем шаге (хотя это и не исключено). В таком случае затруднительно дать оценку погрешности, с которой приближает истинное значение корня 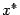, и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство 
, где 
-- желаемая точность нахождения корня. При этом полагают приближённое значение корня равным 
.
Пример 9.8 Решим уравнение 
методом хорд. Зададимся точностью 
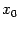и возьмём в качестве начальных приближений и 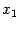концы отрезка, на котором отделён корень: 
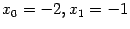. Итерационная формула метода хорд при 
имеет вид
|
По этой формуле последовательно получаем:
Седьмое приближение уже дало нам значение корня с нужной точностью; восьмая итерация понадобилась для того, чтобы убедиться: с заданной точностью значение перестало изменяться. Получаем, что 
.
Упражнение 9.3 Проведите вычисления тем же методом, переставив местами начальные приближения 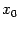и 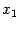, то есть взяв 
. Убедитесь, что получаются другие значения для 
и что с точностью уже 
равняется искомому корню.
Пример 9.9 Проверим, что метод работает и в том случае, есл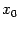и и 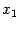взяты по одну и ту же сторону от корня (то есть если корень не отделён на отрезке между начальными приближениями). Возьмём всё для того же уравнения 
и 
. Тогда
Мы получили то же значение 
, причём за то же число итераций. Может показаться, что было бы выгоднее расположить начальные приближения иначе, так чтобы 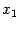было ближе к корню, чем 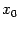. Однако при этом получаем фактически ту же скорость сходимости, можно заметить лишь небольшое ускорение:
Понадобились всё те же семь вычислений.
Вторая разновидность применения формулы (9.3) называется методом ложного положения. Предположим, что корень 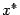отделён на отрезке между 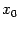и 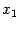, то есть значения 
и 
-- разных знаков. После вычисления по формуле (9.3) на очередном, 
-м, этапе из двух отрезков: между и и между и -- выбирают тот, в концах которого функция принимает значения разных знаков. Если это отрезок между и , то производят перенумерацию предыдущих приближений, то есть полагают равным , а затем повторяют вычисления по формуле (9.3). Этим достигается, что при любом корень 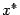располагается на отрезке между и , так что при выполнении условия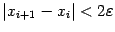 
, где -- желаемая точность нахождения корня, вычисления можно прекратить и взять приближённое значение корня равным . При этом гарантируется, что будет выполнено неравенство 
, то есть корень будет определён с нужной точностью.
Задание