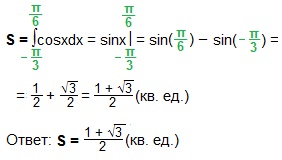Разберите ещё раз примеры решения заданий.

Тема нашего урока: «Вычисление площади криволинейной трапеции с помощью интеграла».

Если заданы границы интегрирования, то мы с вами имеем определенный интеграл:

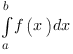
Здесь число - нижний предел интегрирования, число - верхний предел интегрирования. Определенный интеграл - это ЧИСЛО, значение которого вычисляется по формуле Ньютона - Лейбница:

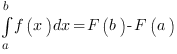
F(a) - это значение первообразной функции f(x) в точке , и, соответственно, F(b) - это значение первообразной функции f(x) в точке b.

Для нас с точки зрения решения задач важное значение имеет геометрический смысл определенного интеграла.

Рассмотрим фигуру, изображенную на рисунке:

 

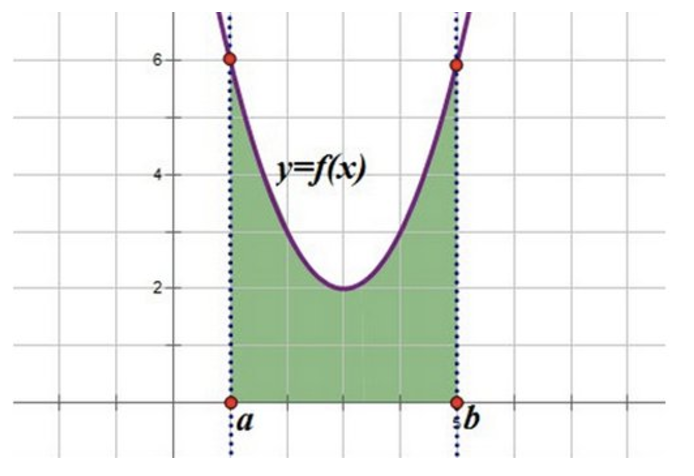
Зеленая фигура, ограниченная сверху графиком функции у=f(x), слева прямой x=a, справа прямой x=b, и снизу осью ОХ называется криволинейной трапецией.

Геометрический смысл определенного интеграла:

Определенный интеграл 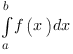- это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху графиком положительной на отрезке

[a; b] функции y=f(x), слева прямой x=a, справа прямой x=b, и снизу осью ОХ.

№1. На рисунке изображён график некоторой функции y=f(x). Функция F(x) = -x³ – 27x² – 240x - 8 — одна из первообразной функции f(x). Найдите площадь закрашенной фигуры.

Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f(x), слева прямой x=-10, справа прямой x=-8, и снизу осью ОХ.

 

Площадь этой криволинейной трапеции вычисляется по формуле:

Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции y= f(x), слева прямой x= -10, справа прямой x= - 8, и снизу осью ОХ.

Площадь этой криволинейной трапеции вычисляется по формуле:

S = 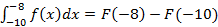, где F(x) - первообразная функции f(x).

 

По условию задачи F(x) = -x³ – 27x² – 240x – 8, поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.

 

Замечу, что в этих задачах очень часто возникают ошибки именно в вычислениях, поэтому советую аккуратно и подробно их записывать, и ничего не считать "в уме".

 

F(-8)= -(-8)³ - 27(-8)² - 240(-8) - 8 =512-1728+1920-8=696

 

F(-10) = -(-10)³ - 27(-10)² - 240(-10) - 8=1000-2700+2400-8=692

 

F(-8) - F(-10) = 696 – 692 = 4

 

Ответ: 4

Разберите ещё раз примеры решения заданий.

№2. Найти площадь криволинейной трапеции, изображенной на рисунке.

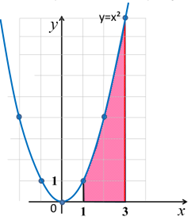
Решение:

Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.

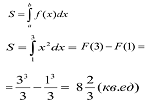
Ответ: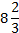

№3. Вычислить определенный интеграл:

Решение: Воспользуемся формулой Ньютона-Лейбница.

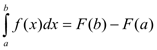
Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b).

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) - F(а), это и будет ответ.

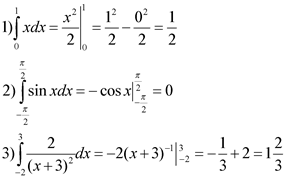
№4. Найти площадь криволинейной трапеции (х-1)², ограниченной линиями х=2 и х=1, осью 0х

Решение:

Воспользуемся формулой Ньютона-Лейбница.

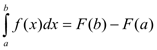
Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b).

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) - F(а), это и будет ответ.

 

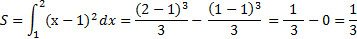
И так, площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):

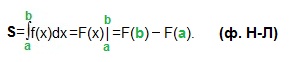
Пример 5. Найти площадь криволинейной трапеции, ограниченной линиями:

y=4x-x²; y=0; x=0; x=4.

Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент, а= -1<0.

Вершина параболы находится в точке O′(m; n), где

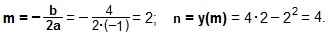
О′(2; 4) – вершина параболы.

Нули функции (точки пересечения графика с осью Ох) найдем из уравнения: 4х-х²=0.

Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4.

Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).

2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.

Площадь построенной криволинейной трапеции находим по (ф. Н-Л).

У нас f (x)=4x-x², a=0, b=4.

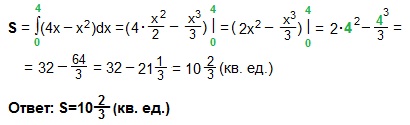
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.

Пример 6. Найти площадь криволинейной трапеции, ограниченной линиями:

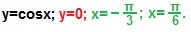
Решение. Строим графики данных линий. (рис. 2).

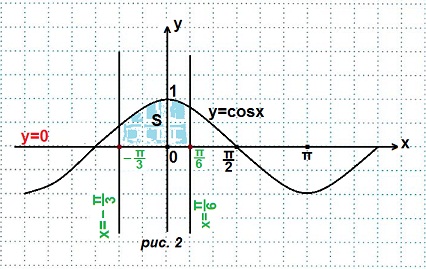
Площадь данной криволинейной трапеции: