Неопределенный интеграл и его свойства. Методы интегрирования
Понятие первообразной функции
В дифференциальном исчислении решается задача: по данной функции 
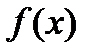найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F’(x) = 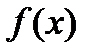(или дифференциал). Искомую функцию F’(x) называют первообразной функции .
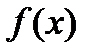Функция F(x) называется первообразной функции 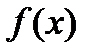на интервале (a;b), если для любого 
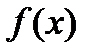(a;b) выполняется равенство:F’(x) = (или dF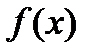(x) = dx);
Например, первообразной функции y = x2, R, является функция F(x) = 
, так как:
F’(x) = ()’ = x2= ;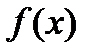
Очевидно, что первообразными будут также любые функции
F(x) = + С;
Где С – постоянная, поскольку
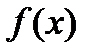F’(x) = ( + С)’ = x2 = , R;
Теорема. Если функция F(x) является первообразной 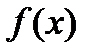на (a;b), то множество всех первообразных для 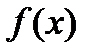задается формулой F(x) + С, где С – постоянное число.
Функция F(x) + С является первообразной 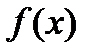. Действительно, (F(x) + С)’ = F’(x) = .
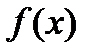Определение неопределенного интеграла
Множество всех первообразных функции F(x) + С для 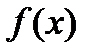называется неопределенным интегралом от функции 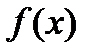и обозначается символом 
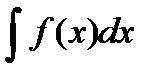. Таким образом, по определению
Здесь 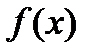называется подынтегральной функцией, 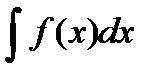- подынтегральным выражением, х – переменной интегрирования, 
- знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Свойства неопределенного интеграла
1. Дифференциал неопределённого интеграла равен подынтегральному выражению, а производная неопределённого интеграла равна подынтегральной функции:
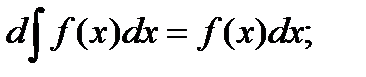
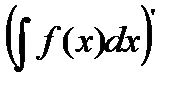
2. Неопределённый интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной:
3. Постоянный множитель подынтегрального выражения можно выносить за знак неопределённого интеграла:
4. Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:
5. Если 
и 
- любая функция, имеющая непрерывную производную, то 
Основные формулы интегрирования
Учитывая, что интегрирование является действием, обратным дифференцированию, то из основных формул дифференцирования легко получить формулы интегрирования. Например, из того, что
следует равенство 
Ниже приведена таблица основных интегралов:
1. 
2. 
где 
3. 
4. 
5. 
6. 
7. 
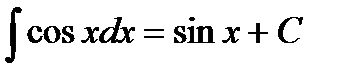
8. 
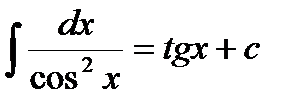
9. 
10. 
11. 
Каждую из формул легко проверить. В результате дифференцирования правой части получается подынтегральное выражение. [1]
Нахождение интеграла непосредственным интегрированием
Рассмотрим примеры нахождения интегралов непосредственным интегрированием: данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам. Полезно применять при этом
также и следующее правило:
если 
то 
.
Пример 1. Найти интеграл 
.
Решение.
= 
- 
+ 
+ 
= 
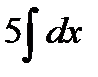+ С1 -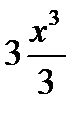 
+ +С2+ 
+ С3 – 5х + С4 = 
- 
+ 
- 5х = С.
где С = С1 +С2 + С3 + С4.
Пример 2. Найти интеграл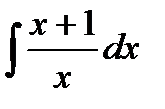 
Решение. =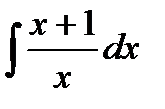 
= 
+ С.
Пример 3. Найти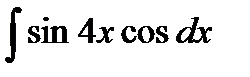 
Решение. Применив формулу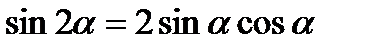 
, получим
Интегрирование способом подстановки (замены переменной)
Непосредственное интегрирование удается сравнительно редко. Поэтому для вычисления интегралов разработан целый ряд приемов, позволяющий сводить данный интеграл к табличному. Одним из наиболее часто используемых приемов является метод подстановки (замены переменной).
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае “удачной” подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 
. Сделаем подстановку х =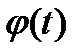 
, где 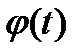-функция, имеющая непрерывную производную.
Тогда 
= 
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой.
= 
. (1)
Формула (1) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого неравенства следует перейти от новой переменной интегрирования 
назад к переменной х.
Иногда целесообразно подбирать подстановку в виде = 
, тогда = 
, где = . Другими словами, формулу (1) можно применять справа налево.
Пример 4. Найти 
Решение. Пусть 
Дифференцируя, получим 
, откуда 
Подставив под знак интеграла вместо 
и 
полученные значения находим 
Заменив 
его выражением через x, получим
Пример 5. Найти 
Решение. Введем подстановку 
Дифференцируя получим 
, откуда 
.
Следовательно:
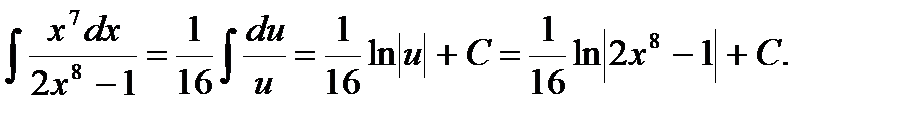
Пример 6. Найти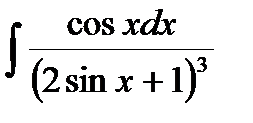 
Решение. Делаем замену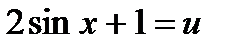 
, дифференцируя, получаем 
, откуда 
Введя новую переменную под знак интеграла, получаем 
Пример 7. Найти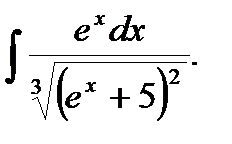 
Решение. Пусть 
тогда 
Следовательно, 