Алгебра 9 класс
Урок № 77
Тема урока: Примеры комбинаторных задач
Цели урока:
обучающие:
· знакомство учащихся с комбинаторикой и комбинаторными задачами,
· формирование у обучающихся умения решать комбинаторные задачи с помощьюперебора возможных вариантов, построения дерева возможных вариантов, составления таблицы, построения графов,
· познакомить учащихся с правилом умножения при решении комбинаторных задач,
развивающие:
· развитие комбинаторного мышления учащихся,
· формирование интеллектуальных умений: анализировать, выделять главное, сравнивать, обобщать и систематизировать, разрешать проблемы,
· развитие умений владеть собой,
· развитие инициативы, уверенности в своих силах, умения преодолевать трудности в учении.
воспитывающие:
· содействовать формированию основных мировоззренческих идей,
· содействовать профориентации учащихся.
Тип урока: урок изучения нового материала.
Ход урока
I. Организационный момент
Учитель: Здравствуйте ребята. Я надеюсь, что наше общение сегодня будет плодотворным и полезным, как для Вас, так и для меня.
II Активизация познавательной деятельности и сообщение темы урока:
Тема нашего урока: «Примеры комбинаторных задач». Запишите её в тетради.
-Ребята, какие задачи мы с вами решали на уроках?
Учащиеся: Мы решали задачи на движение, на проценты, на смеси и сплавы, на составление уравнений и систем уравнений, на работу и производительность, геометрические задачи.
2) Учитель: Почему нам нужно научиться решать комбинаторные задачи? Как вы думаете?
Учащиеся: Потому что в программу 9 класса включен материал: «Элементы комбинаторики и теории вероятностей» и в экзаменационных тестах у нас встречаются задания по этой теме.
3) Учитель: Чтобы вы хотели узнать по теме нашего урока. Поставим вопросы к уроку.
· Чем занимается комбинаторика?
· Какие задачи относятся к комбинаторным?
III. Усвоение новых знаний
Учитель: В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: «Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься». А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Например, учителю приходится распределять различные виды работ между группами учащихся, офицеру выбирать из солдат наряд, агроному размещать культуры на полях и т.д. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый комбинаторикой, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой.
Комбинаторика - раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями.
Слово «комбинаторика » происходит от латинского слова combinare, которое означает «соединять, сочетать». Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике, теории вероятностей и других областях знаний.
Например, в химии (анализ возможных связей между химическими элементами), экономика (анализ вариантов купли-продажи акций), в азартных играх (подсчёт частоты выигрышей), в криптографии (разработка методов шифрования), в доставке почты (рассмотрение вариантов пересылки), в военном деле (расположение подразделений)
Историческая справка
С задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. Некоторые комбинаторные задачи решали в Индии во II веке до н. э., уже несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов, в которых числа располагали так, что сумма по всем вертикалям и главным диагоналям была одной и той же, позднее в Римской империи, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей квадрата и т.д.
Комбинаторными задачами интересовались математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Со временем появились различные игры (нарды, карты, шашки, шахматы и т. д.) Например: обойти всё поле шахматной доски конём. В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных
Как самостоятельный раздел математики комбинаторика оформилась в Европе в XVIII веке. Изучением комбинаторных задач занимались французские математики Б. Паскаль и П. Ферма.
Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ математик Готфрид Вильгельм Лейбниц (1.07.1646 - 14.11.1716), опубликовавший в 1666г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторика».
Леонард Эйлер (1707-1783) рассматривал задачи о разбиении чисел, о паро сочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.
Бурное развитие экономических приложений математики привело к возникновению и изучению обширного класса комбинаторных задач - задач на оптимизацию.
Учитель: Рассмотрим некоторые комбинаторные задачи и способы их решения
Решение комбинаторных задач - это перебор вариантов, подсчет числа вариантов с помощью правила умножения. Если комбинаторная задача имеет несколько решений, то возникает вопрос о подсчете таких решений, возникает проблема оптимального варианта решения задачи.
А) Задачи, решаемые перебором возможных вариантов:
1) Из группы теннисистов, в которую входят четыре человека – Сысоев Даниил, Липин Владислав, Гребеников Артём и Вершинин Кирилл, тренер выделяет двоих для участия в соревнованиях пар. Сколько существует вариантов выбора такой пары?
Решение:
Составим сначала все пары, в которые входит Сысоев (для краткости будем писать первые буквы фамилий). Получим три пары: СЛ, СВ, СГ.
Выпишем теперь пары, в которые входит Липин, но не входит Сысоев. Таких пар две: ЛВ, ЛГ.
Далее составим пары, в которые входит Вершинин, но не входят Липин и Сысоев. Такая пара только одна: ВГ. Других вариантов составления пар нет, так как все пары, в которые входит Гребеников, уже составлены.
Итак, мы получили шесть пар:СЛ, СВ, СГ,ЛВ,ЛГ,ВГ.
Ответ: 6 вариантов.
Б) Задачи, решаемые при помощи построения дерева возможных вариантов:
Однако существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.
№ 714
В кафе предлагают два первых блюда: борщ, рассольник – и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из первого и второго блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Решение: Обед состоит из первого и второго блюда:
Первые блюда: борщ и рассольник Б Р
Вторые блюда: гуляш, котлеты, сосиски, пельмени Г К С П
Итак, мы получили восемь возможных вариантов обедов: БГ, БК, БС, БП, РГ, РК, РС, РП,
Ответ: 8 вариантов.
Г) Задачи, решаемые с помощью построения графа:
4) Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Решение: Задача решается с помощью полного графа с четырьмя вершинами А, Б, В, Г, обозначенными по первым буквам имён каждого из мальчиков. В полном графе проводятся всевозможные рёбра. В данном случае отрезки-рёбра обозначают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 рёбер, значит, и партий сыграно 6 партий.
Ответ: 6 партий.
Е) Задачи, решаемые при помощи комбинаторного правила умножения:
Пусть имеется n элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать способами, после чего второй элемент можно выбрать способами из оставшихся, затем третий элемент можно выбрать способами из оставшихся и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению * * * … *.
5)№ 728
Петр решил пойти на новогодний карнавал в костюме мушкетера. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: пять видов брюк, шесть камзолов, три шляпы, две пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?
Решение: Петр может выбрать брюки пятью способами, камзолы – шестью способами, шляпы – тремя способами и сапоги – двумя. Итак, Петр может составить из этих предметов по комбинаторному правилу умножения 5×6×3×2 =180 различных карнавальных костюмов.
Ответ: 180 карнавальных костюмов.
IV. Применение знаний, умений и навыков в различных ситуациях (стандартных и нестандартных):
6) № 715
У Ирины пять подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?
Решение: Решим задачу перебором возможных вариантов. Составим сначала все пары, в которые входит Вера (для краткости будем писать первые буквы имен девочек). Получим четыре пары: ВЗ, ВМ, ВП, ВС.
Выпишем теперь пары, в которые входит Зоя, но не входит Вера. Таких пар три: ЗМ, ЗП, ЗС.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя. Таких пар только две: МП, МС. Еще осталась пара ПС. Других вариантов составления пар нет.
Итак, мы получили десять пар: ВЗ, ВМ, ВП, ВС, ЗМ, ЗП, ЗС, МП, МС, ПС.
.Ответ:10 вариантов.
8) № 726
Из села Дятлово в село Матвеевское ведут три дороги, а из села Матвеевское в село Першино – четыре дороги. Сколькими способами можно попасть из Дятлово в Першино через Матвеевское
Решение:
Из села Дятлово в село Матвеевское можно послать 3 способами, а из Матвеевского в Першино – 4 способами. Значит, имеются 3 . 4 способа попасть из села Дятлово в село Першино: 3 . 4 = 12 способов.
Ответ: 12 способов.
9) № 718 Составьте все возможные двузначные числа из указанных цифр, используя в записи числа каждую из них не более одного раза: а) 1, 6, 8.
Решение: Построим дерево возможных вариантов:
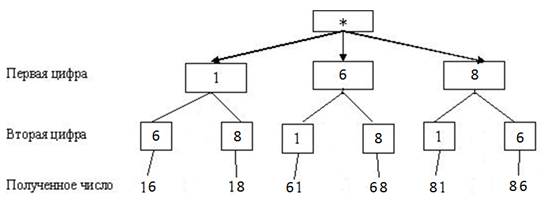
Ответ: 16, 18, 61, 68, 81, 86.
10) № 720. Используя цифры 0, 2, 4, 6, составьте все возможные трехзначные числа, в ко то рых цифры не повторяются.
Решение: Можно построить дерево возможных вариантов. Необходимо помнить, что нуль не может быть первой цифрой в числе, в старший разряд можно поместить цифру 3 способами, в следующий – 3 способами (включая нуль), в последний – 2 способами (из оставшихся двух) Используя комбинаторное правило умножения, получаем: 3 . 3 . 2 = 18 чисел.
Ответ: 18 чисел.
V. Рефлексия.
Учитель:
- Что вы нового узнали сегодня на уроке?
-Что изучает комбинаторика?
-Какие способы решения комбинаторных задач вы знаете?
-Что такое дерево возможных вариантов?
-Когда применить при решении задач правило умножения?
-Как вы думаете, можете ли использовать этот материал в повседневной жизни? Если да, то в какой ситуации.
VI. Домашнее задание: пункт 30 № 714, 716, 717, 718 (б), 721.