Глава 9. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Понятие дифференциала функции
Пусть функция у=f(х) определена на промежутке X и дифференцируема в некоторой окрестности точки 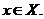 Тогда существует конечная производная
Тогда существует конечная производная

На основании теоремы о связи бесконечно малых величин с пределами функций можно записать

где 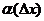 — бесконечно малая величина при
— бесконечно малая величина при  откуда
откуда
 (9.1)
(9.1)
Таким образом, приращение функции 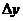 состоит из двух слагаемых: 1) линейного относительно
состоит из двух слагаемых: 1) линейного относительно  2) нелинейного (представляющего бесконечно малую более высокого порядка, чем
2) нелинейного (представляющего бесконечно малую более высокого порядка, чем 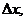 ибо
ибо
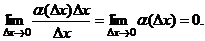
Определение. Дифференциалом функции называется главная, линейная относительно  часть приращения функции, равная произведению производной на приращение независимой переменной
часть приращения функции, равная произведению производной на приращение независимой переменной
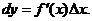 (9.2)
(9.2)
Пример 9.1. Найти приращение и дифференциал функции у=2х2 - 3х при х=10 и 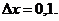
Решение. Приращение функции

Дифференциал функции  При х=10 и
При х=10 и  имеем
имеем 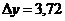 и
и  Различие между
Различие между 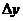 и dy составляет всего 0,02, или 0,5%.
и dy составляет всего 0,02, или 0,5%.
Пример 9.2. Найти дифференциал функции у=х.
Решение.  откуда
откуда 
т.е. дифференциал независимой переменной равен приращению этой переменной.
Поэтому формулу для дифференцирования функции можно записать в виде
dy=f '(x) dx, (9.3)
откуда  Теперь мы видим, что
Теперь мы видим, что  не просто символическое обозначение производной, а обычная дробь с числителем dy знаменателем dx.
не просто символическое обозначение производной, а обычная дробь с числителем dy знаменателем dx.
Геометрический смысл дифференциала. Возьмем на графике функции y=f(x) произвольную точку М(х, у). Дадим аргументу х приращение  Тогда функция у = f(x) получит приращение
Тогда функция у = f(x) получит приращение 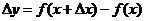 (см.рис. 9.1)
(см.рис. 9.1)

Рис. 9.1 Рис. 9.2
Проведем касательную к кривой у=f(х) в точке М, которая образует угол  с положительным направлением оси Ох, т.е.
с положительным направлением оси Ох, т.е. 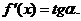 Из прямоугольного треугольника MKN
Из прямоугольного треугольника MKN
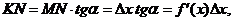
т.е. в соответствии с (9.2) dy=KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции у=f(х) в данной точке, когда х получает приращение  .
.
Не следует думать, что всегда  Так, на рис. 9.2 показан случай, когда
Так, на рис. 9.2 показан случай, когда 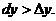
Свойства дифференциала. Свойства дифференциала в основном аналогичны свойствам производной. Приведем их без доказательства:
1. dc=0. 4. d(uv)=v du+u dv
2. d(cu)c du. 5. 
3. 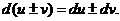
Остановимся теперь на важном свойстве, которым обладает дифференциал функции, но не обладает ее производная.
Инвариантность формы дифференциала. Рассматривая выше y=f(x) как функцию независимой переменной х, мы получили, что dy=f '(x)dx. Рассмотрим функцию y=f(u), где аргумент 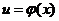 сам является функцией от х, т.е. рассмотрим сложную функцию
сам является функцией от х, т.е. рассмотрим сложную функцию  Если функции y=f(u) и
Если функции y=f(u) и 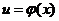 дифференцируемые функции от своих аргументов, то производная сложной функции в соответствии с теоремой, приведенной в 7.4, равна
дифференцируемые функции от своих аргументов, то производная сложной функции в соответствии с теоремой, приведенной в 7.4, равна 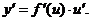
Тогда дифференциал функции
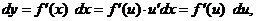
ибо по формуле (9.2) и 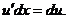 Итак,
Итак,
 (9.4)
(9.4)
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от независимой переменной л рассматривать функцию от зависимой переменной и. Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.
Однако в содержании формул (9.3) и (9.4) все же есть различие: в формуле (9.3) дифференциал независимой переменной равен приращению этой переменной, т.е.  а в формуле (9.4) дифференциал функции du есть лишь линейная часть приращения этой функции
а в формуле (9.4) дифференциал функции du есть лишь линейная часть приращения этой функции 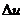 и только при малых
и только при малых 
Применение дифференциала в приближенных вычислениях
Из изложенного выше следует, что  т.е. приращение функции
т.е. приращение функции 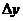 отличается от ее дифференциала dy на бесконечно малую величину более высокого порядка, чем
отличается от ее дифференциала dy на бесконечно малую величину более высокого порядка, чем 
Поэтому при достаточно малых значениях 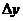
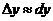 или
или 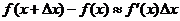 откуда
откуда
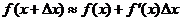 (9.5)
(9.5)
Чем меньше значение 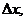 тем точнее формула (9.5).
тем точнее формула (9.5).
Формула (9.5) может оказаться полезной в приближенных вычислениях.
Пример 9.3. Вычислить приближенно: а) 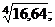 б) tg 46°.
б) tg 46°.
Решение. а) Получим вначале приближенную формулу для вычисления корней любой n -й степени. Полагая 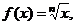 найдем
найдем 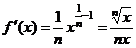 и в соответствии с (9.4)
и в соответствии с (9.4) 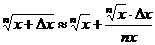 или
или 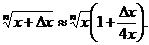 В данном примере
В данном примере

В качестве х возьмем число, наиболее близкое к 16, 64, но чтобы был известен 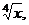 при этом
при этом  должно быть достаточно малым. Очевидно, следует взять х = 16,
должно быть достаточно малым. Очевидно, следует взять х = 16,  =0,64 (но, например, не х = 9,
=0,64 (но, например, не х = 9,  =7,64!). Итак,
=7,64!). Итак, 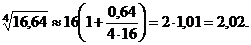
б) Полагая f(x)=tgх, найдем  и в соответствии с (9.4)
и в соответствии с (9.4)  Учитывая, что
Учитывая, что 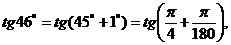 возьмем
возьмем 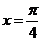 и
и  Тогда
Тогда 
Используя дифференциал, по формуле (9.5) легко получить формулы, часто используемые на практике при 
С помощью дифференциала может быть решена задача определения абсолютной и относительной погрешностей функции по заданной погрешности нахождения (измерения) аргумента.
Пусть необходимо вычислить значение данной функции y=f(x) при некотором значении аргумента xl, истинная величина которого неизвестна, а известно лишь его приближенное значение х с абсолютной погрешностью 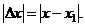 Если вместо истинного значения
Если вместо истинного значения 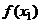 возьмем величину f(х), то мы допустим ошибку, равную
возьмем величину f(х), то мы допустим ошибку, равную 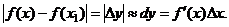
При этом относительная погрешность функции 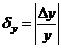 может быть вычислена (при достаточно малых
может быть вычислена (при достаточно малых  ) по формуле:
) по формуле:
 или
или
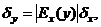 (9.6)
(9.6)
где  — эластичность функции (см. 7.6) (по абсолютной величине);
— эластичность функции (см. 7.6) (по абсолютной величине);  — относительная погрешность нахождения
— относительная погрешность нахождения
Пример 9.4. Расход бензина у (л) автомобиля на 100 км пути в зависимости от скорости х (км/ч) описывается функцией y=18-0,3x-0,003x2. Оценить относительную погрешность вычисления расхода бензина при скорости х=90 км/ч с точностью до 5%.
Решение. Найдем эластичность функции (по абсолютной величине)
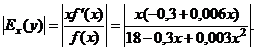 При х=90
При х=90 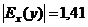 и по формуле (9.5) относительная погрешность
и по формуле (9.5) относительная погрешность 
Пример 9.5. С какой точностью может быть вычислен объем шара, если его радиус измерен с точностью до 2%?
Решение. Объем шара радиуса х равен  Найдем
Найдем 
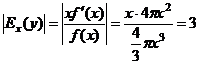 и по формуле (9.6)
и по формуле (9.6) 
Существенным недостатком применения дифференциала в приближенных вычислениях является невозможность вычисления значений функций с наперед заданной точностью. Этого недостатка лишено использование рядов в приближенных вычислениях (см. 14.3).