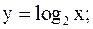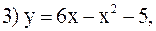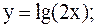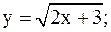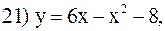Выпуклость и вогнутость
Дифференцируемая функция  называется выпуклой (вогнутой) или выпуклой вверх (вниз) на интервале (a; b), если она удовлетворяет следующему условию: для любых различных точек x1, x2Î(a;b) часть графика функции y = f(x), соответствующая интервалу (x1; x2), расположена выше (ниже) отрезка M1M2, где M1(x1; f(x1)), M2(x2; f(x2)).
называется выпуклой (вогнутой) или выпуклой вверх (вниз) на интервале (a; b), если она удовлетворяет следующему условию: для любых различных точек x1, x2Î(a;b) часть графика функции y = f(x), соответствующая интервалу (x1; x2), расположена выше (ниже) отрезка M1M2, где M1(x1; f(x1)), M2(x2; f(x2)).
 Точка графика функции, разделяющая выпуклый и вогнутый участки графика, называется точкой перегиба (часто точкой перегиба называют абсциссу этой точки графика функции).
Точка графика функции, разделяющая выпуклый и вогнутый участки графика, называется точкой перегиба (часто точкой перегиба называют абсциссу этой точки графика функции).
Теорема 5. Если для функции f(x), дважды дифференцируемой в  (a; b),
(a; b),  (
( ) при всех xÎ(a; b), то функция f(x) является выпуклой (вогнутой) на (a; b).
) при всех xÎ(a; b), то функция f(x) является выпуклой (вогнутой) на (a; b).
Теорема 6. Пусть функция f(x) дважды дифференцируема на (a; b). Точка x0Î(a; b) является точкой перегиба в том и только в том случае, если одновременно выполняются два условия: 1)  ; 2) при переходе через точку x0
; 2) при переходе через точку x0  меняет свой знак.
меняет свой знак.
В последней теореме при условии трижды дифференцируемости функции условие 2) можно заменить на  .
.
Асимптоты
Прямая (L) называется асимптотой графика функции (или просто асимптотой функции), если расстояние d(M; (L)) от точки М на графике функции y = f(x) до прямой (L) стремится к 0 при неограниченном удалении точки М от начала координат.
Различают два вида асимптот: вертикальные и наклонные.
Прямая x = x0 является вертикальной асимптотой, если по крайней мере один из односторонних пределов f(x0 – 0), f(x0 + 0) равен –¥ или +¥.
Наклонная асимптота y = kx + b соответствует случаю x® – ¥ или x® + ¥. Коэффициенты k и b при x® + ¥ находятся из равенств
 ,
, 
(то же при x® – ¥). Если же не существует одного из пределов или один из этих пределов равен – ¥ или + ¥, то у функции отсутствует наклонная асимптота при x® + ¥ (то же при x® – ¥).
Построение графика функции
При построении графика функции сначала проводят исследование функции. При этом придерживаются следующего (примерного) плана:
1) находят область определения функции; 2) указывают точки пересечения с осями координат; 3) определяют точки разрыва и устанавливают тип разрыва; 4) с помощью первой производной устанавливают интервалы монотонности (т.е. интервалы возрастания и убывания) функции и находят точки экстремума и значения функции в этих точках; 5) с помощью второй производной устанавливают интервалы выпуклости, вогнутости и находят точки перегиба; 6) находят асимптоты функции. Затем по этим данным строят график функции.
Пример 3. Построить график функции  .
.
Решение. 1) Нулями знаменателя являются  и
и 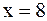 . Следовательно, областью определения функции является множество
. Следовательно, областью определения функции является множество  .
.
2) Найдём точки пересечения с осями координат:
а) c осью 0x. Найдём нули функции:  лишь при x = 0; значит, график функции пересекает ось 0x (или касается оси 0x) в точке O(0; 0) – начале координат;
лишь при x = 0; значит, график функции пересекает ось 0x (или касается оси 0x) в точке O(0; 0) – начале координат;
б) c осью 0y. Для нахождения общей точки графика функции и оси 0y следует найти f(0): f(0) = 0. Поэтому график пересекает ось 0y в точке O(0; 0).
3) Наша функция представляет собой отношение двух многочленов, поэтому она непрерывна всюду, за исключением нулей знаменателя:  и x = 8. Найдём левые и правые пределы в этих точках.
и x = 8. Найдём левые и правые пределы в этих точках.
Для точки  :
:

 ;
;

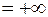 .
.
Отсюда делаем вывод, что  является точкой разрыва второго рода.
является точкой разрыва второго рода.
Для точки x = 8:

 ;
;

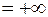 .
.
Поэтому x = 8 также является точкой разрыва второго рода.
4) Имеем

Критическими точками функции являются её стационарные точки  ,
,  ,
,  . Знак
. Знак 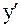 совпадает со знаком выражения
совпадает со знаком выражения  .
.

Видно, что функция возрастает на промежутках  и
и  и убывает на промежутках
и убывает на промежутках 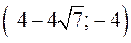 ,
, 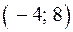 ,
, 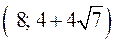 . Следовательно, точка
. Следовательно, точка  является точкой максимума (на рисунке ей соответствует «горка»), точка
является точкой максимума (на рисунке ей соответствует «горка»), точка  – точкой минимума (ей соответствует «впадина»). Стационарная точка
– точкой минимума (ей соответствует «впадина»). Стационарная точка  не является точкой экстремума. Найдём значение функции в точках экстремума: f(
не является точкой экстремума. Найдём значение функции в точках экстремума: f(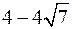 ) » –7,57; f(
) » –7,57; f( ) » 25,35.
) » 25,35.
5)  .
.
Трёхчлен  при всех x (его дискриминант меньше 0). Поэтому знак
при всех x (его дискриминант меньше 0). Поэтому знак  совпадает со знаком дроби
совпадает со знаком дроби  .
.
Составим схему. Видно, что функция выпукла в интервалах (–¥; –4)

и (0; 8) и вогнута в интервалах (–4; 0) и (8; +¥). При переходе через точки – 4, 8, 0  меняет свой знак. Поэтому точка x = 0 является точкой перегиба (в точках x = - 4, x = 8 функция не определена).
меняет свой знак. Поэтому точка x = 0 является точкой перегиба (в точках x = - 4, x = 8 функция не определена).
6) Так как  ,
,  , то прямые
, то прямые  и
и
x = 8 являются вертикальными асимптотами. Найдём наклонные асимптоты при x ® –¥ и при x ® +¥. Уравнения этих асимптот будем искать в виде y = kx + b:
а) x ® –¥.
 ,
,

Таким образом, прямая y = x + 4 является асимптотой при x ® –¥;
б) при x ® +¥ получим тот же результат: прямая y = x + 4 является асимптотой.
Основываясь на полученных данных, построим график функции.

Пример 4. Построить график функции  .
.
Решение. 1) Областью определения функции является (–¥; +¥).
2) Найдём точки пересечения с осями координат:
а) c осью 0x. Функция не имеет нулей, следовательно, она не имеет общих точек с осью 0x;
б) c осью 0y. Имеем  . Точка (0; e-4) является точкой пересечения графика с осью 0y.
. Точка (0; e-4) является точкой пересечения графика с осью 0y.
3) Наша функция является суперпозицией непрерывных функций, поэтому она непрерывна на всей числовой оси.
4) Имеем
 .
.
 Функция имеет одну стационарную точку
Функция имеет одну стационарную точку 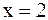 . Функция
. Функция  возрастает на промежутке (–¥; 2) и убывает на промежутке (2; +¥), точка x = 2 является точкой максимума. Максимум функции равен
возрастает на промежутке (–¥; 2) и убывает на промежутке (2; +¥), точка x = 2 является точкой максимума. Максимум функции равен  .
.
5)  .
.
Функция  имеет нули x1=2–
имеет нули x1=2– 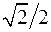 , x2=2+
, x2=2+ 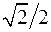 . Она выпукла на интервале
. Она выпукла на интервале
(2– 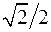 ; 2+
; 2+  ) и вогнута на интервалах (–¥; 2–
) и вогнута на интервалах (–¥; 2– 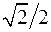 ), (2+
), (2+ 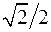 ; + ¥). Точки x = 2 –
; + ¥). Точки x = 2 – 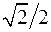 и x = 2 +
и x = 2 + 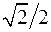 являются точками перегиба.
являются точками перегиба.
6) Так как функция определена и непрерывна на всей числовой оси, то она не имеет вертикальных асимптот. Найдём наклонные асимптоты.
а) x ® –¥. Ищем асимптоту в виде y = kx + b.
 ,
,
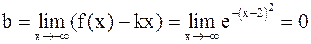 .
.
Таким образом, прямая  является асимптотой функции при
является асимптотой функции при
x ® –¥.
б) При x ® +¥ получим тот же результат:  является асимптотой при x ® +¥.
является асимптотой при x ® +¥.
По полученным данным построим график функции.

Пример 5. Построить график функции 
Решение. 1) Область определения функции 
 ,
,  .
.
2) Точки пересечения с осями координат
 ;
; 
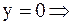
 ;
;  ;
;
 ;
; 
3) Функция непрерывна на всей области определения.
4) 
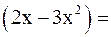




Следовательно, производная 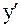 в точке
в точке  не определена.
не определена.
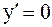 ,
,  ,
,  стационарная точка.
стационарная точка.

Функция убывает на промежутках  и возрастает на промежутке
и возрастает на промежутке 

Следовательно, точка 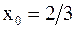 является точкой максимума;
является точкой максимума;  критическая точка, является точкой минимума.
критическая точка, является точкой минимума.

 ,
,

График данной функции приведен на рисунке.

5. Элементарные преобразования графиков
Напомним некоторые приемы, которые часто используются при построении графиков функций. Пусть построен график функции  . Тогда:
. Тогда:
1) график функции  получается из графика функции
получается из графика функции  переносом вдоль оси 0X на a единиц влево, если
переносом вдоль оси 0X на a единиц влево, если  , или на
, или на 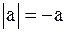 единиц вправо, если
единиц вправо, если  ;
;
2) график функции  получается из графика функции
получается из графика функции  переносом на b единиц вверх, если b > 0, или на
переносом на b единиц вверх, если b > 0, или на 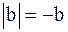 единиц вниз, если
единиц вниз, если  ;
;
3) график функции 
 получается из графика функции
получается из графика функции  сжатием вдоль оси 0X в
сжатием вдоль оси 0X в  раз, если
раз, если  , или растяжением в
, или растяжением в  раз, если
раз, если 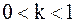 ;
;
4) график функции  получается из графика функции
получается из графика функции 
 растяжением вдоль оси 0Y в c раз, если
растяжением вдоль оси 0Y в c раз, если 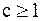 (при
(при  сжатием в
сжатием в  раз);
раз);
5) графики функций  и
и  симметричны относительно оси 0Y; графики функций
симметричны относительно оси 0Y; графики функций  и
и  симметричны относительно оси 0X.
симметричны относительно оси 0X.
Пример 6. Построить график функции 


а б
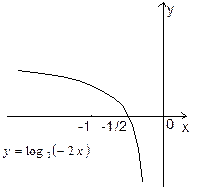

в г
Подчеркнем, что величина сдвига вдоль оси 
 определяется той постоянной, которая прибавляется непосредственно к аргументу
определяется той постоянной, которая прибавляется непосредственно к аргументу  , а не к аргументу
, а не к аргументу  . Поэтому для нахождения этой постоянной функцию
. Поэтому для нахождения этой постоянной функцию  преобразуют к виду
преобразуют к виду  . Здесь сдвиг вдоль оси
. Здесь сдвиг вдоль оси  на
на  единиц.
единиц.
Например,  . Значит, график функции
. Значит, график функции  получается из графика функции
получается из графика функции 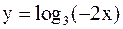 переносом вдоль оси
переносом вдоль оси  на
на  единиц вправо.
единиц вправо.
Пример 7. Построить график функции
 .
.

а

б
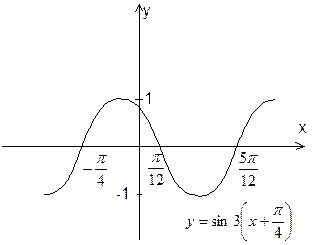
в

г
Отметим также следующее. Пусть заданы функция  и ее график. Тогда выражения
и ее график. Тогда выражения  ,
,  и
и  определяются следующим образом:
определяются следующим образом:




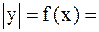

Графики этих функций приведены на рисунках, представленных ниже.


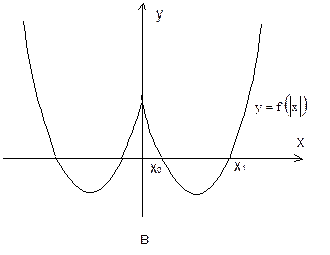

Задание 6.1
Для заданной функции f(x) = x4 + px3 + qx2 + rx +c и отрезка
[a; b] (коэффициенты приведены в таблице) найдите:
а) промежутки возрастания, убывания и точки экстремума;
б) наибольшие и наименьшие значения функции на отрезке [a; b].
| № варианта | p | q | r | c | a | b |
| –8 | –144 | –5 | –10 | |||
| –8/3 | –2 | |||||
| 16/3 | –24 | –4 | ||||
| 8/3 | –10 | –40 | –2 | |||
| –16/3 | –1 | –2 | ||||
| 8/3 | –3 | |||||
| 32/3 | –2 | –32 | –3 | –3 | ||
| –4/3 | –12 | –3 | ||||
| –8 | –48 | –4 | ||||
| 4/3 | –18 | –36 | –2 | |||
| 20/3 | –32 | –1 | –3 | |||
| –28/3 | –8 | |||||
| 20/3 | –4 | –40 | –1 | –3 | ||
| 16/3 | –8 | –64 | –3 | |||
| 16/3 | –18 | –144 | –4 | |||
| 4/3 | –8 | –16 | –3 | –3 | ||
| Окончание таблицы | ||||||
| № варианта | p | q | r | c | a | b |
| 28/3 | –3 | |||||
| –24/3 | –24 | |||||
| –16 | –96 | –1 | ||||
| 8/3 | –18 | –72 | –1 | –3 | ||
| –26 | –2 | |||||
| –6/3 | –1 | |||||
| –1 | –2 | |||||
| –2 | –12 | –2 | ||||
| –14 | –3 | –3 | ||||
| –4/3 | –20 | –3 | ||||
| –8/3 | –10 | –2 | –2 | |||
| –20/3 | –1 | |||||
| –4/3 | –8 | –4 | ||||
| –4/3 | –4 | –5 | –2 |
Задание 6.2
Исследовать и построить графики функций:
a)  ; б)
; б)  .
.
Коэффициенты В, С приведены в таблице, n – номер варианта (в задании б) точное нахождение точек перегиба не предполагается).
| № вар. | |||||||||||||||||||||||||||||
| В | –2 | –1 | –2 | ||||||||||||||||||||||||||
| С | |||||||||||||||||||||||||||||
| № вар. | |||||||||||||||||||||||||||||
| В | –1 | –4 | –3 | –2 | –1 | –5 | –3 | –4 | –4 | –3 | –2 | ||||||||||||||||||
| С | |||||||||||||||||||||||||||||
Задание 6.3
Построить графики функций с помощью производной первого порядка.
1)  15)
15) 
2)  ; 16)
; 16)  ;
;
3)  17)
17)  ;
;
4)  18)
18)  ;
;
5)  19)
19)  ;
;
6)  ; 20)
; 20)  ;
;
7)  21)
21)  ;
;
8)  ; 22)
; 22)  ;
;
9)  ; 23)
; 23)  ;
;
10)  ; 24)
; 24)  ;
;
11) 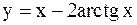 ; 25)
; 25) 
12)  ; 26)
; 26)  ;
;
13)  ; 27)
; 27)  ;
;
14)  ; 28)
; 28)  ;
;
29)  ; 30)
; 30)  .
.
Задание 6.4
Исследовать и построить графики функций.
1)  16)
16) 
2)  17)
17) 
3)  18)
18) 
4) 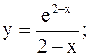 19)
19) 
5) 
 20)
20) 
6)  21)
21) 
7)  22)
22) 
8) 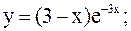 23)
23) 
9)  24)
24) 
10)  25)
25) 
11)  26)
26) 
12)  27)
27) 
13)  28)
28) 
14)  29)
29) 
15)  30)
30) 
Задание 6.5
Исследовать и построить графики функций.
1)  16)
16) 
2)  17)
17) 
3)  18)
18) 
4)  19)
19) 
5)  20)
20) 
6)  21)
21) 
7)  22)
22) 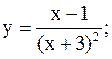
8)  23)
23) 
9)  24)
24) 
10)  25)
25) 
11) 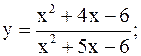 26)
26) 
12)  27)
27) 
13)  28)
28) 
14)  29)
29) 
15)  30)
30) 
Задание 6.6
Построить графики функций  ;
;  ;
;  ;
;  ;
;  ;
;  , взяв данные
, взяв данные  ,
,  ,
,  ,
,  ,
, 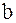 ,
,  ,
,  в таблице (№ – номер варианта)
в таблице (№ – номер варианта)
| № | 
| 
| 
| 
| 
| 
| 
|

| 
| ||||||

| –3 | ||||||

| 
| 
| |||||

| 
| –2 | |||||

| –5 | –3 | |||||

| 
| 
| –3 | ||||
| –2 | –1 | ||||||

| 
| –7 | |||||

| 
| –4 | –1 | –1 | |||
| –7 | |||||||

| 
| –6 | –2 | ||||

| –7 | ||||||

| –2 | –8 | |||||

| –8 | –4 | |||||

| –1 | ||||||
| –3 | 
| –2 | |||||

| –7 | ||||||

| –3 | ||||||
| Окончание таблицы | |||||||
| № | 
| 
| 
| 
| 
| 
| 
|

| –4 | –7 | |||||
| –2 | 
| –3 | –1 | ||||

| –5 | ||||||

| –3 | –8 | |||||

| 
| 
| –1 | –1 | |||

| –4 | ||||||

| –2 | –7 | |||||

| –25 | –15 | |||||

| –4 | ||||||

| –7 | ||||||

| –1 | –1 |
Задание 6.7
Построить графики следующих функций:
1)  7)
7) 
2)  8)
8) 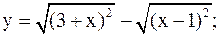
3)  9)
9) 
4)  10)
10) 
5)  11)
11) 
6)  12)
12) 
13)  22)
22) 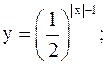
14)  23)
23) 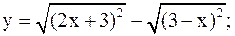
15)  24)
24) 
16)  25)
25) 
17)  26)
26) 
18)  27)
27) 
19)  28)
28) 
20)  29)
29) 
21) 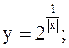 30)
30) 
Задание 6.8
Построить графики следующих функций:
а) y = f(x); б) y =  ; в) y = f(
; в) y = f( ); г)
); г)  = f(x);
= f(x);
д) y =  ; е)
; е)  ; ж)
; ж)  .
.