Лекция
Задание: изучить материал лекции и выписать по одному примеру на вычисление площади фигуры и вычисление объёма тела.
1. Вычисление площадей плоских фигур.
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
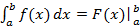= F(a)-F(b)
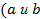- соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:
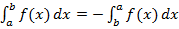
2. Отрезок интегрирования можно разбивать на части:
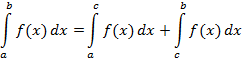
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1.
= 
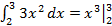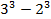=27-8=19.
 |
у
+ +
0 a - b x
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула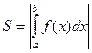 
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример 2
Вычислить площадь фигуры, ограниченной линиями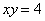 
, 
, 
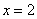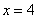и осью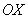 
Решение:
Выполним чертеж: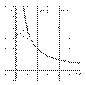 
На отрезке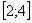 
график функции 
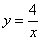расположен над осью 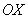, поэтому:
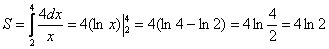
Ответ: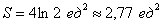 
Примечание: В задачах на нахождение площадей преподаватели часто требуют записывать ответ не только точно, но и, в том числе, приближенно.
Пример 3
Вычислить площадь фигуры, ограниченной линиями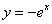 
, 
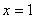и координатными осями.
Решение: Выполним чертеж:
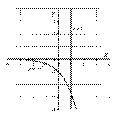
Если криволинейная трапеция полностью расположена под осью 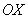, то её площадь можно найти по формуле: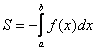 
В данном случае:
Ответ: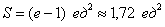 
Пример 4
Найти площадь плоской фигуры, ограниченной линиями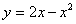 
, 
.
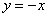Решение: Сначала нужно выполнить чертеж. При построении чертежа в задачах на площадь нас интересуют точки пересечения линий. Найдем точки пересечения параболы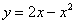 
и прямой 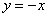. Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
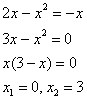
Нижний предел интегрирования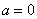 
, верхний предел интегрирования 
.
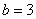Можно построить линии поточечно, при этом пределы интегрирования выясняются по чертежу.
Выполним чертеж:
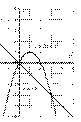
Искомая фигура ограничена параболой 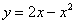сверху и прямой 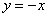снизу.
На отрезке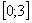 
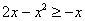, по соответствующей формуле:
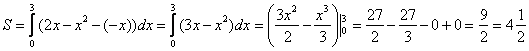
Ответ: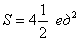 
Пример 5 Вычислить площадь фигуры, ограниченной линиями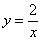 
, 
, 
, 
.
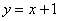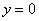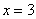Решение: Сначала выполним чертеж:
1) На отрезке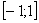 
над осью 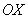расположен график прямой ;
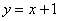2) На отрезке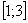 
над осью 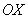расположен график гиперболы .
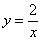Совершенно очевидно, что площади можно приплюсовать, поэтому:
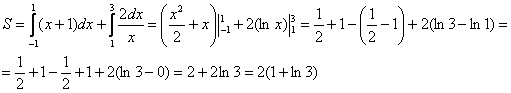
Ответ: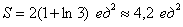 
Пример 6
Вычислить площадь фигуры, ограниченной линиями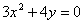 
, 
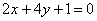
Представим уравнения в виде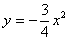 
, 
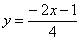и выполним поточечный чертеж:
Найдем точки пересечения прямой 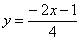и параболы .
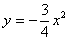Для этого решаем уравнение:
, 
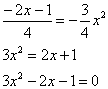
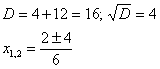
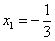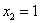
Действительно,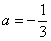 
.
На отрезке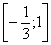 
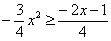, по соответствующей формуле:
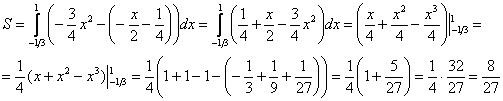
Ответ: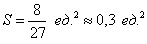 
2. Вычисление объемов тел.
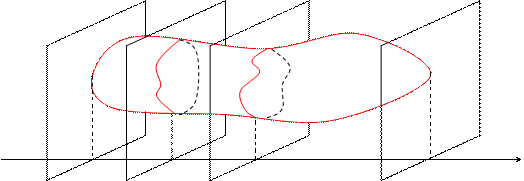
Вычисление объема тела по известным площадям его параллельных сечений.
Q(xi-1)
Q(xi)
a xi-1 xi b x
Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны MiDxi и miDxi здесь Dxi = xi - xi-1.
Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно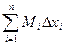 
и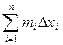 
.
При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:
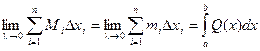
Таким образом, объем тела может быть найден по формуле:
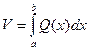
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.
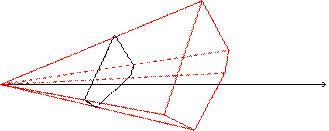
Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S.
 |
Q S
x H x
При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.
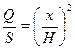
Отсюда получаем функцию площадей сечений: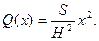 
Находим объем пирамиды: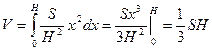 
3. Объем тел вращения.
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
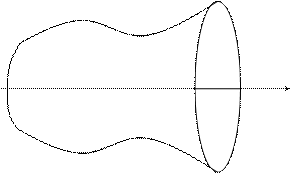y = f(x)
x
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса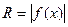 
, то объем тела вращения может быть легко найден по полученной выше формуле:
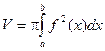
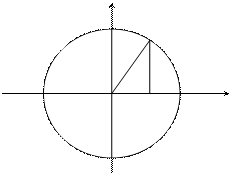Пример: Найти объем шара радиуса R.
y
R y
-R 0 x R x
В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле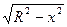 
.
Тогда функция площадей сечений имеет вид: Q(x) =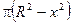 
.
Получаем объем шара:
.
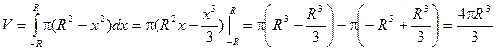